人教版2021年秋季九年级上册期末复习训练试卷 word版，含答案

人教版2021年秋季九年级上册期末复习训练试卷

知识范围：九上及九下第26章

一、选择题

1．下列汽车标志中既是轴对称图形又是中心对称图形的是（　　）

A． B． C． D．

2．抛物线y＝（x﹣2）2＋3的顶点坐标是（    ）

A．（2，3） B．（﹣2，3） C．（2，﹣3） D．（﹣2，﹣3）

3．如果2是方程的一个根，则常数的值是（    ）

A．1 B．2 C．－1 D．－2

4．已知正比例函数的图象与反比例函数图象相交于点，下列说法正确的是（    ）

A．反比例函数的解析式是         B．两个函数图象的另一交点坐标为

C．当或时，            D．正比例函数与反比例函数都随的增大而增大

5．已知反比例函数 y＝的图象如图所示，则二次函数 y =ax 2－2x和一次函数 y＝bx+a 在同一平面直角坐标系中的图象可能是（      ）

A．B．C．D．

6．如图，在中，，将绕点A按顺时针方向旋转，对应得到，则的度数为（    ）

A． B． C． D．

7．若A（﹣3，y1），C（1，y2）在二次函数y＝x2+2x+c的图象上，则y1，y2的关系是（　　）

A． B． C． D．无法确定

8．若关于x的一元二次方程x2＋x﹣m＝0有实数根，则m的取值范围是（    ）

A． B． C． D．

9．如图，四边形ABCD内接于⊙O，若它的一个外角∠DCE＝65°，则∠A的度数为（　　）

A．112° B．68° C．65° D．52°

10．如图，抛物线与x轴交于点（3，0），对称轴为直线x＝1．结合图象分析下列结论：①；②；③一元二次方程的两根分别为；④．其中正确的结论有（　   　）个 

A．1 B．2 C．3 D．4

二、填空题

11．抛物线y＝x2﹣6x+2的对称轴为直线_____．

12．在英语句子“Wish you success”（祝你成功）中任选一个字母，这个字母为“s”的概率是_____．

13．已知一个圆锥体的三视图如图所示，将这个圆锥的侧面展开为扇形，则这个扇形的圆心角是_____．

14．如图，在⊙O中，AB是直径，CD是⊙O的切线，直线AB和ED交于点C，∠ADE＝60°，则∠C的度数为__________．

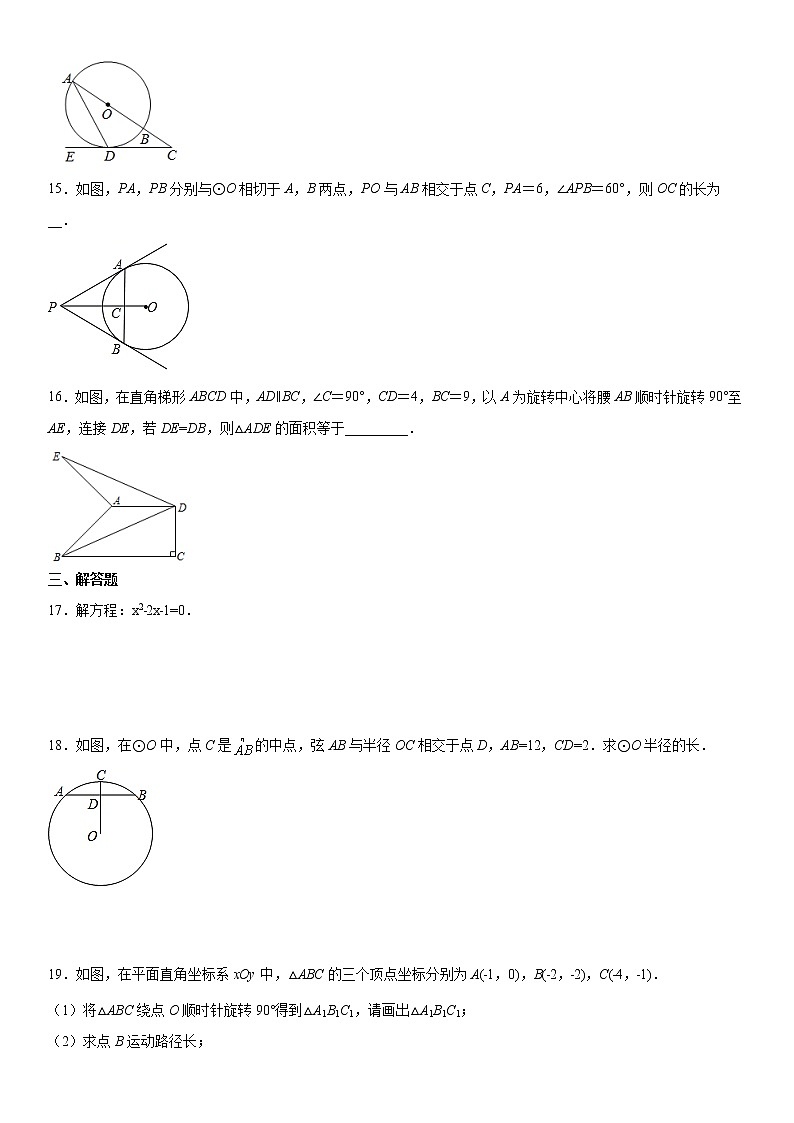
15．如图，PA，PB分别与⊙O相切于A，B两点，PO与AB相交于点C，PA＝6，∠APB＝60°，则OC的长为__．

16．如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，CD＝4，BC＝9，以A为旋转中心将腰AB顺时针旋转90°至AE，连接DE，若DE=DB，则△ADE的面积等于_________．

三、解答题

17．解方程：x2﹣2x﹣1=0．

18．如图，在⊙O中，点C是的中点，弦AB与半径OC相交于点D，AB=12，CD=2．求⊙O半径的长．

19．如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A(﹣1，0)，B(﹣2，﹣2)，C(﹣4，﹣1)．

（1）将△ABC绕点O顺时针旋转90°得到△A1B1C1，请画出△A1B1C1；

（2）求点B运动路径长；

20．为庆祝中华人民共和国建国70周年，某校从A、B两位男生和D、E两位女生中选派学生，参加全区中小学“我和我的祖国”演讲比赛．

（1）如果选派一位学生参赛，那么选派到的代表是A同学的概率是    　；

（2）如果选派两位学生参赛，用树状图或列表法，求恰好选派一男一女两位同学参赛的概率．

21．如图，已知抛物线经过A（-3，0）、C（0，-3）两点．

（1）求b，c的值；

（2）求抛物线与x轴的另一个交点B的坐标，并结合图象，写出当时，x的取值范围．

22．如图，将△ABC绕点A按顺时针方向旋转90°，得到△ADE，点B的对应点为点D，点C的对应点E落在BC边上，连接BD．

（1）求证：DE⊥BC；

（2）若AC=3，BC=7，求线段BD的长．

23．某超市销售一种饮料，平均每天可售出100箱，每箱利润12元，为了扩大销售，增加利润，超市准备适当降价，据测算，每箱每降价1元，平均每天可以多售出20箱．

（1）若要使每天销售该饮料获利1400元，则每箱应降价多少元？

（2）每箱降价多少元超市每天获利最大？最大利润是多少？

24．如图，一次函数和反比例函数的图象相交于两点，点的横坐标为2．

（1）求的值及，两点的坐标

（2）当时，求的取值范围．

25．如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC=AB，⊙O为△ABC的外接圆．

（1）如图1，求证：AD是⊙O的切线；

（2）如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G．

①求证：AG=BG；②若AD=4，CD=5，求GF的长．

参考答案

1．C

【分析】

直接利用轴对称图形和中心对称图形的概念求解．

【详解】

解：A、是轴对称图形，不是中心对称图形，故此选项不合题意；

B、是轴对称图形，不是中心对称图形，故此选项不合题意；

C、既是中心对称图形也是轴对称图形，故此选项符合题意；

D、是轴对称图形，不是中心对称图形，故此选项不合题意；

故选：C．

【点睛】

本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．

2．A

【分析】

直接利用顶点式的特点可写出顶点坐标．

【详解】

解：顶点式，顶点坐标是，

的顶点坐标是．

故选：A．

【点睛】

本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在中，对称轴为，顶点坐标为．

3．D

【分析】

把x=2代入已知方程列出关于的新方程，通过解方程来求的值．

【详解】

解：∵2是一元二次方程的一个根，
∴22-2+ =0，
解得， =-2．
故选：D．

【点睛】

本题考查的是一元二次方程的解的定义．一元二次方程的解，就是使方程左右两边相等的未知数的值．

4．C

【分析】

由题意可求正比例函数解析式和反比例函数解析式，由正比例函数和反比例函数的性质可判断求解．

【详解】

解：正比例函数的图象与反比例函数的图象相交于点，

正比例函数，反比例函数

两个函数图象的另一个角点为

，选项错误

正比例函数中，随的增大而增大，反比例函数中，在每个象限内随的增大而减小，

选项错误

当或时，

选项正确

故选C．

【点睛】

本题考查了反比例函数与一次函数的交点问题，熟练运用反比例函数与一次函数的性质解决问题是本题的关键．

5．C

【分析】

先根据抛物线y=ax2-2x过原点排除A，再由反比例函数图象确定ab的符号，再由a、b的符号和抛物线对称轴确定抛物线与直线y=bx+a的位置关系，进而得解．

【详解】

∵当x=0时，y=ax2-2x=0，即抛物线y=ax2-2x经过原点，故A错误；

∵反比例函数y=的图象在第一、三象限，

∴ab＞0，即a、b同号，

当a＜0时，抛物线y=ax2-2x的对称轴x=＜0，对称轴在y轴左边，故D错误；

当a＞0时，b＞0，直线y=bx+a经过第一、二、三象限，故B错误；

C正确．

故选C．

【点睛】

本题主要考查了一次函数、反比例函数、二次函数的图象与性质，根据函数图象与系数的关系进行判断是解题的关键，同时考查了数形结合的思想．

6．B

【分析】

根据旋转可得∠CAC′=50°，再根据角之间的和差关系可得答案．

【详解】

解：∵将△ABC绕点A按顺时针方向旋转50°，

∴∠CAC′=50°，

∵∠BAC=32°，

∴∠C′AB=50°+32°=82°，

故选：B．

【点睛】

本题考查了旋转的性质，关键是掌握对应点与旋转中心所连线段的夹角等于旋转角．

7．B

【分析】

利用二次函数图象上点的坐标特征可求出y1，y2的值，比较后即可得出结论．

【详解】

解：∵点A（-3，y1）、C（1，y2）是二次函数y=x2+2x+c图象上的两点，

∴y1=3+c，y2=3+c．

∴，

故选：B．

【点睛】

本题考查了二次函数图象上点的坐标特征，利用二次函数图象上点的坐标特征求出y1，y2的值是解题的关键．

8．B

【分析】

根据方程有实数根得出不等式，求出不等式的解集即可．

【详解】

解：关于的一元二次方程有实数根，

，

解得：，

故选：B．

【点睛】

本题考查了根的判别式和解一元一次不等式，能根据根的判别式和已知得出不等式是解此题的关键．

9．C

【分析】

圆的内接四边形内对角互补．

【详解】

解：由题意得，∠A+∠BCD=180°，

又∠DCE +∠BCD=180°，

所以∠A=∠DCE=65°，

故选：C．

【点睛】

本题考查圆的内接四边形，是基础考点，掌握相关知识是解题关键．

10．B

【分析】

根据二次函数图象的开口方向、对称轴、顶点坐标、增减性以及二次函数与一元二次方程的关系，逐项判断即可．

【详解】

解：抛物线开口向下，因此a＜0，对称轴为x＝1＞0，因此a、b异号，所以b＞0，抛物线与y轴交点在正半轴，因此c＞0，所以abc＜0，故①不正确；
当x＝2时，y＝4a＋2b＋c＞0，故②正确；
抛物线与x轴交点（3，0），对称轴为x＝1．因此另一个交点坐标为（−1，0），即方程ax2＋bx＋c＝0的两根为x1＝3，x2＝−1，故③正确；
抛物线与x轴交点（−1，0），所以a−b＋c＝0，又x＝＝1，有2a＋b＝0，所以3a＋c＝0，而a＜0，因此2a＋c＞0，故④不正确；
故选：B．

【点睛】

本题考查二次函数的图象和性质，掌握二次函数的a、b、c的值决定抛物线的位置是正确判断的关键．

11．x＝3

【分析】

把解析式化为顶点式可求得答案．

【详解】

∵y＝x2﹣6x+2＝（x﹣3）2﹣7，

∴对称轴是直线x＝3，

故答案为：x＝3．

【点睛】

本题考查二次函数性质，求对称轴可以利用顶点式求，也可以直接利用对称轴公式直接求对称轴。

12．

【详解】

试题解析：在英语句子“Wishyousuccess!”中共14个字母，其中有字母“s”4个．故其概率为.

考点：概率公式．

13．216°

【分析】

根据展开图的扇形的弧长等于圆锥底面周长计算．

【详解】

解：观察三视图得：圆锥的底面半径为3cm，高为4cm，

所以圆锥的母线长为5cm，

，

解得n=216°．

故答案为：216°．

【点睛】

考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．

14．30°

【分析】

连接OD，根据切线的性质求出∠ADC和∠ODA，从而得到∠OAD的度数，再根据三角形内角和定理求解即可．

【详解】

解：如图所示，连接OD，

∵EC是圆O的切线，

∴∠ODE=∠ODC=90°，

∵∠ADE=60°，

∴∠ADO=30°，∠ADC=120°

∵OA=OD，

∴∠OAD=∠ODA=30°，

∴∠C=180°-∠DAC-∠ADC=30°，

故答案为：30°．

【点睛】

本题主要考查了切线的性质，等腰三角形的性质，三角形内角和定理，解题的关键在于能够熟练掌握切线的性质．

15．

【分析】

根据切线的性质和切线长定理可得OA⊥PA，∠APO=30°，PA=PB，根据直角三角形的性质可得OA=2CO，根据勾股定理可求AO的长，即可求OC的长．

【详解】

解：如图，连接OA，

∵PA，PB分别与⊙O相切于A，B两点，PA=6，∠APB=60°，

∴OA⊥PA，∠APO=30°，PA=PB，

∴∠AOC=60°，AB⊥PO

∴∠CAO=30°

∴AO=2CO，

在中，

∴

∵

∴

∴

∴CO=

故答案为：．

【点睛】

本题考查了切线的性质，切线长定理，勾股定理等知识，熟练运用切线的性质是本题的关键．

16．10

【分析】

连接BE，延长DA，由旋转的性质可得AE=AB，∠BAE=90°，可证AD垂直平分BE，可得AM⊥BE，BM=ME=AM，则可证四边形DCBM是矩形，可得BC=MD=9，BM=CD=4，即可求解．

【详解】

解：如图，连接BE，延长DA，

∵以A为旋转中心将腰AB顺时针旋转90°至AE，
∴AE=AB，∠BAE=90°，
∴∠ABE=∠AEB=45°，
∵DE=DB，AE=AB，
∴AD垂直平分BE，
∴AM⊥BE，BM=ME=AM，
∵AD∥BC，∠C=90°，
∴∠ADC=90°，BC⊥BE，
∴四边形DCBM是矩形，
∴BC=MD=9，BM=CD=4，
∴AM=BM=4=EM，
∴AD=MD-AM=5，
∴△ADE的面积=×AD×EM=×5×4=10，
故答案为：10．

【点睛】

本题考查了旋转的性质，线段垂直平分线的性质，矩形的判定和性质，添加恰当辅助线构造矩形是本题的关键．

17．.

【分析】

方法一：确定a、b、c的值，判断△的值，最后根据求根公式求解；

方法二：运用配方法解题.

【详解】

解法一：

解法二:

故答案是

【点睛】

本题考查的是解一元二次方程的能力，能够根据题目特点灵活采取合适的方法解题.

18．10

【详解】

试题分析：连接OA，根据垂径定理求出AD=6，∠ADO=90°，根据勾股定理得出方程，求出方程的解即可．

试题解析：连接AO，

∵点C是弧AB的中点，半径OC与AB相交于点D，

∴OC⊥AB，

∵AB=12，

∴AD=BD=6，

设⊙O的半径为r，

∵CD=2，

∴在Rt△AOD中，由勾股定理得：AD2=OD2+AD2，

即：r2=（r﹣2）2+62，

∴r=10，

答：⊙O的半径长为10．

19．（1）见解析；（2）

【分析】

（1）利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1，从而得到△A1B1C1；

（2）根据B运动的路径长为弧BB1，利用弧长公式求解即可得到答案．

【详解】

解：（1）如图，△A1B1C1即为所求；

（2）如图所示，B运动的路径长为弧BB1的长，

由题意得∠BOB1=90°

∵B（-2，-2）

∴ ,

∴ ．

∴点B运动路径长为．

【点睛】

本题主要考查了画旋转图形，求弧长，解题的关键在于能够熟练掌握相关知识进行求解．

20．（1）；（2）表格见详解，概率为

【分析】

（1）因为总人数为4人，所以选派到的代表是A同学的概率是 ；

（2）将所有的情况列在表格中，然后找出一男一女的情况数，最后利用概率公式求解即可.

【详解】

（1）因为参赛的总人数为4人，所以选派到的代表是A同学的概率是 ；

故答案为；

（2）列表如下：

共有12种等可能的结果，其中恰好为一男一女的结果有8种，故恰好选派一男一女两位同学参赛的概率为

【点睛】

本题主要考查树状图或列表法求随机事件的概率，掌握树状图或列表法是解题的关键.

21．（1）；（2）

【分析】

（1）运用待定系数法将A（-3，0）、C（0，-3）两点的坐标代入抛物线解析式，即可得出b，c的值；

（2）根据x轴上的点的纵坐标为零，令，求出的值即可得出B的坐标，结合图像，直接写出当时，x的取值范围即可．

【详解】

解：（1）将（-3，0），（0，-3）代入得：

，

解得：，

∴b，c的值分别为2，-3；

（2）由（1）可知抛物线的解析式为，

当时，，

解得：，

∴抛物线与x轴的另一个交点B的坐标为（1，0），

由图象可知当时，．

【点睛】

本题考查了待定系数法求二次函数解析式，根据函数值的范围求自变量取值范围等知识点，解题的关键是熟练运用数形结合的思想解题．

22．（1）证明见解析；（2）5．

【分析】

（1）由旋转的性质可得AC=AE，∠CAE=90°，∠AED=∠ACE，可得∠ACE=∠AEC=45°=∠AED，可得结论；
（2）由直角三角形的性质可求EC=6，可求BE=1，由勾股定理可求BD的长．

【详解】

（1）∵将△ABC绕点A按顺时针方向旋转90°，

∴AC=AE，∠CAE=90°，∠AED=∠ACE，

∴∠ACE=∠AEC=45°=∠AED，

∴∠DEC=90°，

∴DE⊥BC；

（2）∵AE=AC=3，∠EAC=90°，

∴EC=6，

∴BE=BC﹣EC=1．

∵将△ABC绕点A按顺时针方向旋转90°，

∴DE=BC=7，

∴DB==5．

【点睛】

本题考查了旋转的性质，勾股定理等知识，掌握旋转的性质是本题的关键．

23．（1）2元或5元；（2）每箱降价3.5元时获利最大，最大利润是1445元

【分析】

（1）设每箱应降价元，列方程解答；

（2）设每天获利元，由题意得到，化为顶点式即可得到答案．

【详解】

解：（1）要使每天销售饮料获利1400元，设每箱应降价元，依据题意列方程得，

，

整理得，

解得，；

答：要使每天销售该饮料获利1400元，则每箱应降价2元或5元．

（2）设每天获利元，

则，

，

，

每箱降价3.5元时获利最大，最大利润是1445元．

【点睛】

此题考查一元二次方程的实际应用，二次函数的实际应用，二次函数的性质，正确理解题意是解题的关键．

24．（1）；（2）或

【分析】

（1）将x=2代入求得A（2，3），将A（2，3）代入求得，解方程组得到B点的坐标为（-6，-1）；
（2）反比例函数与一次函数的交点坐标即可得到结论．

【详解】

解：（1）将代入，

得，

∴．

将代入，

得，

∴，

∴，

解得（舍去）或．

将代入，

得,

∴．

（2）由图可知，当时，或．

【点睛】

此题考查反比例函数与一次函数的交点问题，正确的理解题意是解题的关键．

25．（1）见解析；（2）①见解析；②

【分析】

（1）连接OA，OB，OC，由AC＝AB，OA＝OA，OC＝OB可证出△OAC≌△OAB（SSS），利用全等三角形的性质可得出∠OAC＝∠OAB，即AO平分∠BAC，利用垂径定理可得出AO⊥BC，结合AD∥BC可得出AD⊥AO，由此即可证出AD是⊙O的切线；
（2）①连接AE，由圆内接四边形对角互补结合∠BCE＝90°可得出∠BAE＝90°，由同角的余角相等可得出∠BAG＝∠AEB，结合∠ABC＝∠ACB＝∠AEB可得出∠BAG＝∠ABC，再利用等角对等腰可证出AG＝BG；
②由∠ADC＝∠AFB＝90°，∠ACD＝∠ABF，AC＝AB可证出△ADC≌△AFB（AAS），利用全等三角形的性质可求出AF，BF的长，设FG＝x，在Rt△BFG中，利用勾股定理可求出x的值，此题得解．

【详解】

证明：（1）连接OA、OB、OC，如图1，

∵AC=AB，OA=OA，OC=OB，

∴△OAC≌△OAB，

∴∠OAC＝∠OAB，

∴AO⊥BC，

∵AD∥BC，

∴AD⊥AO，

∴AD是⊙O的切线；

（2）①连接AE，如图2，

∵AD∥BC，AD⊥CD，

∴BC⊥CD，

∴∠BCE＝90°，

∴BE是直径，

∴∠BAE＝90°，

∴∠BAG+∠EAF＝90°，

又∵AF⊥BE，

∴∠AEB+∠EAF＝90°，

∴∠BAG=∠AEB，

∵∠ABC=∠ACB=∠AEB，

∴∠BAG=∠ABC，

∴AG=BG；

②∵AC=AB，∠ACD＝∠ABF，∠ADC=∠AFB＝90°，

∴△ADC≌△AFB，

∴AF=AD=4，BF=CD=5，

设FG=x，则AG=GB=x+4，

在Rt△BFG中，由勾股定理可得：

，

解得：，

∴．

【点睛】

本题是圆的综合题，考查了切线的判定，全等三角形的判定与性质，垂径定理，圆周角定义，平行线的性质，圆内接四边形，等腰三角形的判定以及勾股定理，解题的关键是：（1）利用全等三角形的性质及垂径定理，找出AO⊥BC；（2）①利用等角的余角相等及圆周角定理，找出∠BAG＝∠ABC；②在Rt△BFG中，利用勾股定理求出FG的长．