人教版新课标A选修4-1第一讲 相似三角形的判定及有关性质三 相似三角形的判定及性质教案设计

这是一份人教版新课标A选修4-1第一讲 相似三角形的判定及有关性质三 相似三角形的判定及性质教案设计，共6页。教案主要包含了目的要求，知识要点，重点和难点分析，典型例题等内容，欢迎下载使用。
相似三角形的判定 【目的要求】1.使学生理解相似三角形和相似比的概念，掌握相似三角形的判定定理，会灵活运用这些定理解决一些简单的证明和计算问题。会按已知相似比作一个三角形与已知三角形相似。通过相似三角形判定定理的学习，要求了解类比方法的作用，认识类比方法是获取新知识的一种重要方法。 【知识要点】    一、相似三角形1.相似三角形定义：对应角相等，对应边成比例的三角形，叫做相似三角形。2.相似三角形的表示方法：用符号“∽”表示，读作“相似于”。3.相似三角形的相似比：相似三角形的对应边的比叫做相似比。4.相似三角形的预备定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所截成的三角形与原三角形相似。5.相似三角形的判定定理：(1)如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似，（简叙为两角对应相等两三角形相似）。(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似（简叙为：两边对应成比例且夹角相等，两个三角形相似。）(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似（简叙为：三边对应成比例，两个三角形相似。）6.直角三角形相似的判定定理：(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。7.相似三角形的性质定理：(1)相似三角形的对应角相等。(2)相似三角形的对应边成比例。(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。(4)相似三角形的周长比等于相似比。(5)相似三角形的面积比等于相似比的平方。相似三角形的传递性如果△ABC∽△A1B1C1，△A1B1C1∽△A2B2C2，那么△ABC∽A2B2C2 【重点和难点分析】重点：1.相似三角形的有关概念及相似三角形的基本定理。(1) 相似三角形的定义中突出的一个特征是“形状相同但大小不一定相同”，这是和全等三角形的重点区别，以下表中我们也可以看出： 图    形对应角对应边全等三角形∠A=∠A′∠B=∠B′∠C=∠C′AB=A′B′AC=A′C′BC=B′C′相似三角形∠A=∠A′∠B=∠B′∠C=∠C′（K为任意正实数）全等三角形是相似三角形的一种特殊情况，即相似比为1。(2) 表示两个三角形相似时注意通常要把表示对应顶点的字母写在相应的位置上，这样比较容易找到相似三角形的对应角和对应边。    例如：图2
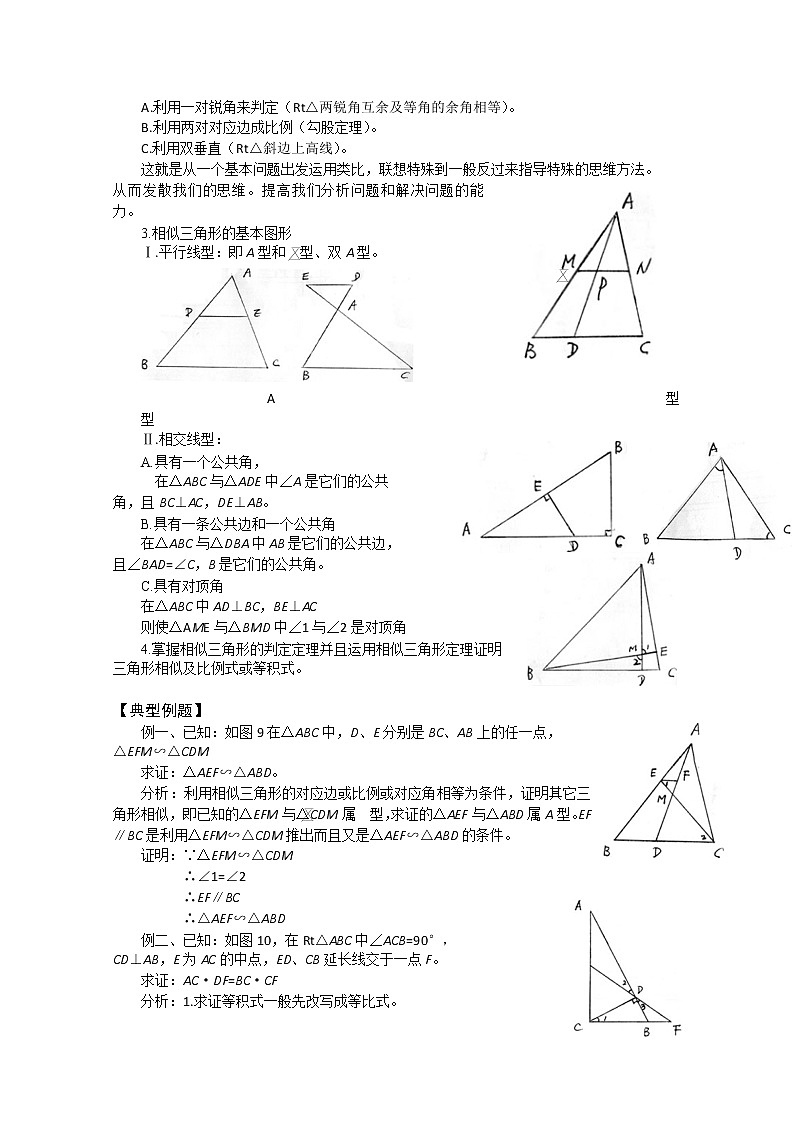
图中A对应着P，B对应着M，C对应着N。因此两个三角形相似应写为△ABC∽△PMN。(3) 相似三角形的基本定理，它是相似三角形的一个判定定理，也是后面学习的相似三角形的判定定理的基础，这个定理确定了相似三角形的两个基本图形“A”型和“  ”型。在利用定理证明时要注意A型图的比例，每个比的前项是同一个三角形的三条边，而比的后项是另一个三角形的三条对应边，它们的位置不能写错，尤其是要防止写成的错误。2.相似三角形的判定定理。(1)三角形相似的判定方法与全等的判定方法的联系列表如下：类型斜三角形直角三角形全等三角形的判定SASSSSAAS（ASA）HL相似三角形   的判定两边对应成比例夹角相等三边对应成比例两角对应相等一条直角边与斜边对应成比例从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理，这就是我们数学中的用类比的方法，在旧知识的基础上找出新知识并从中探究新知识掌握的方法。(3)在掌握相似三角形的判定方法的基础上我们再看Rt△相似判定的特殊性。A.利用一对锐角来判定（Rt△两锐角互余及等角的余角相等）。B.利用两对对应边成比例（勾股定理）。C.利用双垂直（Rt△斜边上高线）。这就是从一个基本问题出发运用类比，联想特殊到一般反过来指导特殊的思维方法。从而发散我们的思维。提高我们分析问题和解决问题的能力。相似三角形的基本图形Ⅰ.平行线型：即A型和  型、双A型。
                  A型                                       型Ⅱ.相交线型：    具有一个公共角，  在△ABC与△ADE中∠A是它们的公共角，且BC⊥AC，DE⊥AB。    具有一条公共边和一个公共角在△ABC与△DBA中AB是它们的公共边，且∠BAD=∠C，B是它们的公共角。具有对顶角在△ABC中AD⊥BC，BE⊥AC则使△AME与△BMD中∠1与∠2是对顶角掌握相似三角形的判定定理并且运用相似三角形定理证明三角形相似及比例式或等积式。 【典型例题】例一、已知：如图9在△ABC中，D、E分别是BC、AB上的任一点，△EFM∽△CDM求证：△AEF∽△ABD。分析：利用相似三角形的对应边或比例或对应角相等为条件，证明其它三角形相似，即已知的△EFM与△CDM属  型，求证的△AEF与△ABD属A型。EF∥BC是利用△EFM∽△CDM推出而且又是△AEF∽△ABD的条件。证明：∵△EFM∽△CDM      ∴∠1=∠2      ∴EF∥BC∴△AEF∽△ABD例二、       已知：如图10，在Rt△ABC中∠ACB=90°，CD⊥AB，E为AC的中点，ED、CB延长线交于一点F。求证：AC·DF=BC·CF分析：1.求证等积式一般先改写成等比式。       2.从求证的结论看四条线段分别在△ABC、△DCF中但很明显两个三角形不相似，在这样的情况下一般需要找一个过渡比（或叫做中间比）通过证两对三角形相似来证明。证明：在△ABC与△CBD中      ∵∠ACB=90°，CD⊥AB，∠B=∠B∴△ABC∽△CBD∴，∠A=∠1∵E是AC中点，CD⊥AB∴AE=EC=ED∴∠A=∠2∵∠2=∠3、∠A=∠1∴∠3=∠1在△FBD与△FDC中∵∠F=∠F、∠3=∠1∴即∴∴AC·DF=BC·CF例三、已知：如图11，△ABC中M、E分别是AC、AB上的点，ME、CB延长线交于一点D，且。求证：AM=DB分析：当图形中不存在明显的成比例线段的基本图形时，应考虑添加适当的辅助线构造出基本图形创造代换条件。证明：过M作MN∥DC      ∴      ∵          ∴           ∴AM=DB例四、已知：AD是Rt△ABC中∠A的平分线，∠C=90°，EF是AD的垂直平分线交AD于M，EF、BC的延长线交于一点N。求证：(1)△AME∽△NMD      (2)ND2=NC·NB分析：1.本题要应用“等量代替”公理，线段的等量代替是证等积式或等比式的桥梁，体现在：      (1)AD是∠CAB的平分线，∠1=∠2，∠1，∠N是同角余角，得∠1=∠N，∠2=∠N从而解决△AME∽△NMD证明。(2) EF所在直线是AD的垂直平分线，通过添加辅助线连结NA，NA=ND，使证明ND2=NC·NB，变为证NA2=NC·NB。证明：(1)连结NA        ∵AD是∠BAC的平分线        ∴∠1=∠2        ∵NE是AD的垂直平分线        ∴∠5=∠6=90°，NA=ND        ∵∠ACB=90°        ∴∠1=∠4        ∴∠2=∠4        ∴△AME∽△NMD(2) ∵NA=ND，NM⊥AD∴∠3=∠4  ∴2∠4=2∠2，即∠ANC=∠CAB  ∴∠7=∠B，∠ANC=∠ANC  ∴△NAC∽△NBA  ∴           ∴NA2=NC·NB           即ND2=NC·NB例五、       已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。求证：EB·DF=AE·DB分析：1.求证等积式一般先将其化为等比式，使问题转化为求证等比式，再将求证等比式转化为求证两个三角形相似。证明△ABE∽△FBE的条件；已具备的条件是∠ABE=∠FBD，再证一对对应角相等的条件难找，因此改证夹这对角的四条边成比例。证明：∵AC⊥BC，CD⊥AB      ∴∠BDC=∠ACB=90°      ∴∠B=∠B，△CDB∽△ACB      ∴      即BC2=AB·DB      ∵CF⊥BE      ∴∠EFC=∠ECB=90°      ∵∠2=∠2∴△BCF∽△BEC∴即BC2=BE·BF∵AB·DB=BE·BF即∴∠3=∠2∴△BAE∽△BFD          ∴          ∴BE·DF=AE·BD