数学选修2-13.2立体几何中的向量方法随堂练习题

这是一份数学选修2-13.2立体几何中的向量方法随堂练习题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
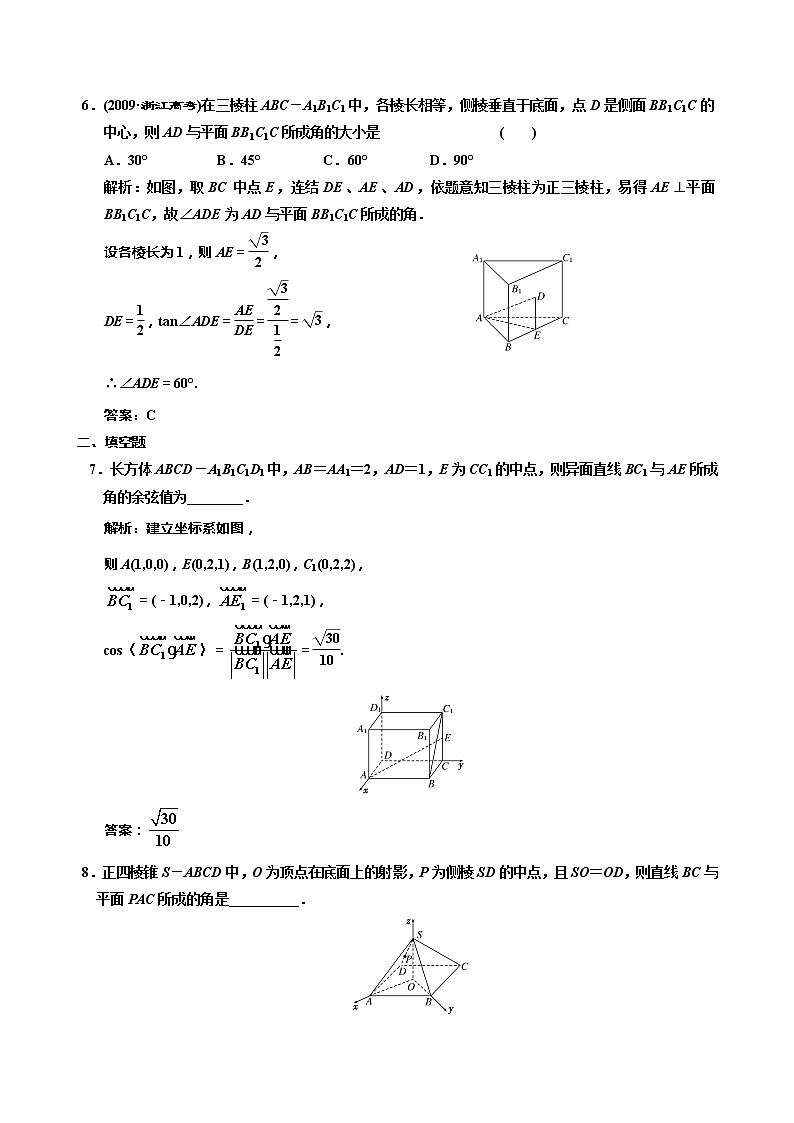
立体几何中的向量方法课下练兵场 命 题 报 告      难度及题号知识点容易题(题号)中等题(题号)稍难题(题号)利用空间向量证明 平行、垂直问题111 利用空间向量求异面   直线所成角、线面角.2、34、6、78利用空间向量求二面角510、129 一、选择题1．若直线l的方向向量为a，平面α的法向量为n，能使l∥α的是                 (　　)A．a＝(1,0,0)，n＝(－2,0,0)              B．a＝(1,3,5)，n＝(1,0,1)C．a＝(0,2,1)，n＝(－1,0，－1)           D．a＝(1，－1,3)，n＝(0,3,1)解析：若l∥α，则a·n＝0.而A中a·n＝－2，B中a·n＝1＋5＝6，C中a·n＝－1，只有D选项中a·n＝－3＋3＝0.答案：D2．若向量a＝(1，λ，2)，b＝(2，－1,2)，且a与b的夹角余弦值为，则λ等于(　　)A．2　　　　　　　B．－2         C．－2或           D．2或－解析：cos〈a，b〉＝＝＝，λ＝－2或.答案：C3．在正方体ABCD－A1B1C1D1中，M为DD1的中点，O为底面ABCD的中心，P为棱A1B1上任意一点，则直线OP与直线AM所成的角是                      (　　)A.              B.           C.              D.解析：(特殊位置法)将P点取为A1，作OE⊥AD于E，连接A1E，则A1E为OA1在平面AD1内的射影，又AM⊥A1E，∴AM⊥OA1，即AM与OP成90°角．或建系利用向量法． 答案：D4．(2009·全国卷Ⅱ)已知正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，E为AA1中点，则异面直线BE与CD1所成角的余弦值为                                     (　　)A.                B.          C.               D. 解析：如图连结A1B，则有A1B∥CD1， ∠A1BE就是异面直线BE与CD1所成角，设AB=1，则A1E=AE=1，∴BE=，A1B=.由余弦定理可知：cos∠A1BE=答案：C5．(2009·滨州模拟)在正方体ABCD－A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为                                (　　)A.             B.            C.            D.解析：以A为原点建系，设棱长为1.则A1(0,0,1)，E(1,0，)，D(0,1,0)，∴＝(0,1，－1)， ＝(1,0，－)，设平面A1ED的法向量为n1＝(1，y，z)则∴∴n1＝(1,2,2)，∵平面ABCD的一个法向量为n2＝(0,0,1)．∴cos〈n1，n2〉＝＝.即所成的锐二面角的余弦值为.答案：B6．(2009·浙江高考)在三棱柱ABC－A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是                 (　　)A．30°          B．45°         C．60°         D．90° 解析：如图，取BC中点E，连结DE、AE、AD，依题意知三棱柱为正三棱柱，易得AE⊥平面BB1C1C，故∠ADE为AD与平面BB1C1C所成的角．设各棱长为1，则AE＝，DE＝，tan∠ADE＝＝＝，∴∠ADE＝60°.答案：C二、填空题7．长方体ABCD－A1B1C1D1中，AB＝AA1＝2，AD＝1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为________．解析：建立坐标系如图，则A(1,0,0)，E(0,2,1)，B(1,2,0)，C1(0,2,2)， ＝(－1,0,2)，＝(－1,2,1)，cos〈〉＝＝.答案：8．正四棱锥S－ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面PAC所成的角是__________．解析：如图，以O为原点建立空间直角坐标系O-xyz.设OD=SO=OA=OB=OC=a， 则A(a,0,0)，B(0，a,0)，C(-a,0,0)，P(0，)，则＝(2a,0,0)，＝(－a，－，)，＝(a，a,0)，设平面PAC的法向量为n，可求得n＝(0,1,1)，则cos〈，n〉＝＝＝，∴〈，n〉＝60°，∴直线BC与平面PAC所成的角为90°－60°＝30° 答案：30°9．正三棱锥的一个侧面的面积与底面积之比为2∶3，则这个三棱锥的侧面和底面所成二面角的度数为________．解析：设一个侧面面积为S1，底面面积为S，则这个侧面在底面上射影的面积为，由题设得＝，设侧面与底面所成二面角为θ，则cosθ＝＝＝，  ∴θ＝60°.答案：60°三、解答题10．(2009·包头模拟)如图，四棱锥P－ABCD的底面是矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD，E为侧棱PD的中点． (1)求证：PB∥平面EAC；(2)若AD＝AB，试求二面角A－PC－D的正切值．解：法一：(1)证明：连接BD交AC于点O，连接OE，在△PDB中，OE∥PB，又OE⊂平面AEC，PB⊄平面AEC，故PB∥平面AEC.(2)设AD=AB=PD=PA=a，∵侧面PAD⊥底面ABCD，又CD⊥AD，∴CD⊥侧面PAD，∴AE⊥DC，又△PAD为正三角形，且E为PD中点，∴AE⊥PD，故AE⊥平面PDC 在等腰△PDC中，作DM⊥PC，则M为PC的中点，再作EN∥DM交PC于点N，则EN⊥PC，连接AN，则∠ANE为二面角A-PC-D的平面角，在Rt△PDC中，DM=a，所以EN=a，在等边△PAD中，AE=a，所以tan∠ANE=法二：(1)证明：如图建立空间直角坐标系O-xyz，其中O为AD的中点．设PA=AD=PD=a，AB=b，则P(0,0，a)，D(－，0,0)，E(－，0，a)，B(，b,0)，连接BD交AC于点F，则F(0，，0)．＝(，，－a)，＝(，b，－a)＝2，∴∥，又EF⊂平面AEC，且PB⊄平面AEC，∴PB∥平面EAC.(2)设PA＝AD＝PD＝AB＝a，则P(0,0，a)，A (，0,0)，C(－，a,0)，D(－，0,0)． ＝(－a，a,0)，＝(－，a，－a)， ＝(－，0，－a)，设n1＝(x1，y1，z1)是平面PAC的法向量，则即令z1＝1，解得x1＝y1＝，∴n1＝(，，1)，设n2＝(x2，y2，z2)是平面PCD的法向量， 则即令z2＝1，解得x2＝－，y2＝0，∴n2＝(－，0,1)，cos〈n1，n2〉＝＝－，设所求二面角的平面角为α，则cosα＝，sinα＝，tanα＝.11．(2010·江苏苏北三市模拟)如图，在四棱锥P—ABCD中，底面ABCD为直角梯形，AB∥CD，∠BAD＝90°，PA⊥平面ABCD，AB＝1，AD＝2，PA＝CD＝4.(1)求证：BD⊥PC；(2)求二面角B—PC—A的余弦值．解析：(1)证明：以A为原点，建立如图所示空间直角坐标系，则B(0,1,0)，C(-2,4,0)，D(-2,0,0)，P(0,0,4)，∴ (－2,4，－4)，＝(－2，－1,0)，∴＝4－4＝0，所以PC⊥BD (2)易证为平面PAC的法向量，＝(－2，－1,0)．设平面PBC的法向量n＝(a，b，c)，＝(0,1，－4)，＝(－2,3,0)，所以⇒所以平面PBC的法向量n＝(6,4,1)，∴cosθ＝＝＝－.因为平面PAC和平面PBC所成的角为锐角，所以二面角B—PC—A的余弦值为12．(2009·湖北五市调研)如图甲，直角梯形ABCD中，AB∥CD，∠DAB＝，点M、N分别在AB，CD上，且MN⊥AB，MC⊥CB，BC＝2，MB＝4，现将梯形ABCD沿MN折起，使平面AMND与平面MNCB垂直(如图乙)．(1)求证：AB∥平面DNC； (2)当DN的长为何值时，二面角D－BC－N的大小为30°？ 解：法一：(1)证明：∵MB∥NC，MB⊄平面DNC，NC⊂平面DNC，∴MB∥平面DNC.同理MA∥平面DNC，又MA∩MB=M，且MA、MB⊂AB∥平面DNC.(2)过N作NH⊥BC交BC延长线于H，∵平面AMND⊥平面MNCB，DN⊥MN，∴DN⊥平面MBCN，从而DH⊥BC，∴∠DHN为二面角D-BC-N的平面角．由MB=4，BC=2，∠MCB=90°知∠MBC=60°，CN=4-2cos60°=3，∴NH=3sin60°=.由条件知：tan∠NHD=∴DN=NH法二：如图，以点N为坐标原点，以NM，NC，ND所在直线分别作为x轴，y轴和z 轴，建立空间直角坐标系N-xyz，易得NC=3，MN=，设DN=a，则D(0,0，a)，C(0,3,0)，B(,4,0)，M(,0,0)，A(,0，a)． (1)证明：∵＝(0,0，a)，＝(0,3,0)，＝(0,4，－a)．∴＝－(0,0，a)＋(0,3,0)＝－＋，∵ND，NC⊂平面DNC，且ND∩NC＝N，∴与平面DNC共面，又AB⊄平面DNC，∴AB∥平面DNC.(2)设平面DBC的法向量n1＝(x，y， z)，＝(0,3，－a)，＝(，1,0) 则，令x＝－1，则y＝，z＝.∴n1＝(－1，，)．又平面NBC的法向量n2＝(0,0,1)．∴cos〈n1，n2〉＝＝＝.即：＝.∴a2＝，又a＞0，∴a＝，即DN＝.