


- 2.4 点到直线的距离(第一课时)课件 课件 12 次下载
- 2.4 点到直线的距离(第二课时)课件 课件 12 次下载
- 2.5.1 圆的标准方程 课件 课件 13 次下载
- 2.5.2 圆的一般方程 课件 课件 13 次下载
- 2.5 圆的方程 同步练习 试卷 9 次下载
高中数学湘教版(2019)选择性必修 第一册2.4 点到直线的距离教课内容课件ppt
展开2.4 点到直线的距离(练习)
一.单项选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点到直线的距离为
A. B. C. D.
【答案】A
【解析】点到直线的距离
.故选A.
2.直线与直线平行,则与之间的距离为
A. B. C. D.
【答案】D
【解析】直线可化为,
因为与直线平行,所以,即,
所以与之间的距离为故选D.
3.已知,则的最小值为
A. B. C. D.
【答案】C
【解析】表示到上点的距离的平方,
所以的最小值是(0,0)到的距离的平方,
据点到直线的距离公式得,所以的最小值为.故选C.
4.直线和直线的夹角平分线的方程为
A. B.
C.或 D.或
【答案】D
【解析】设为角平分线上的任意一点,由该点到两直线的距离相等,即可得:
,即,
整理得或.故选D.
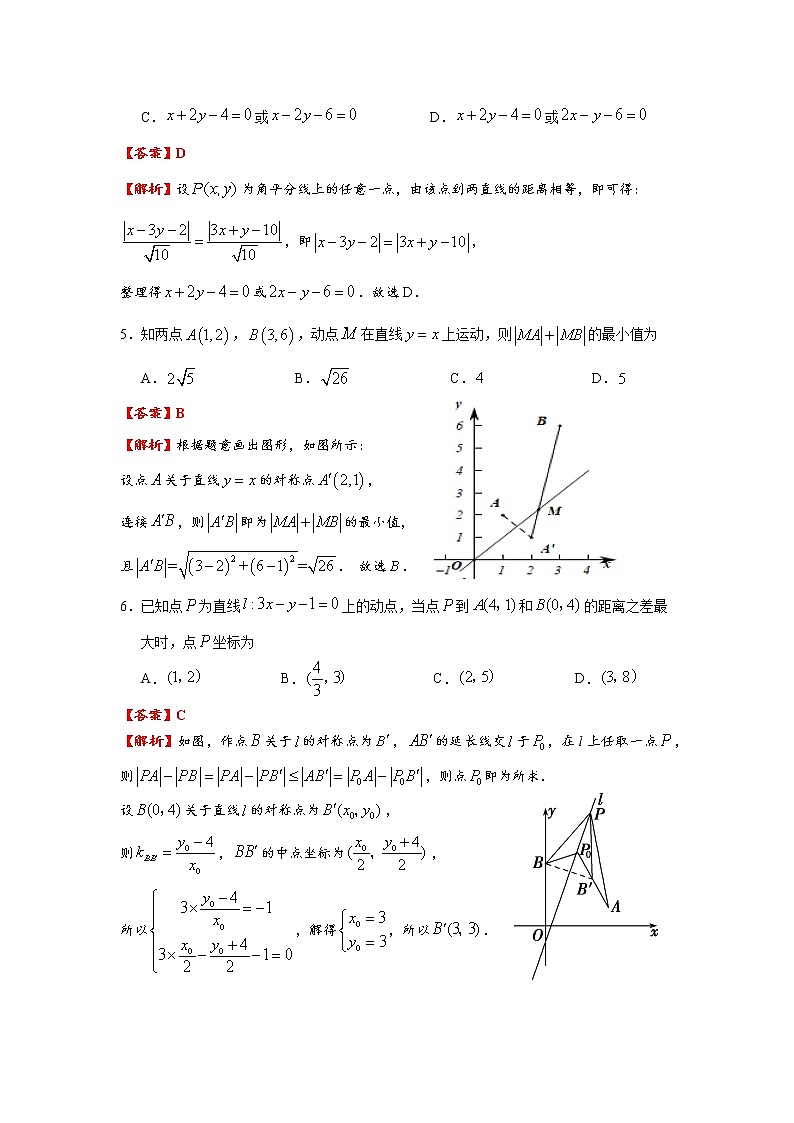
5.知两点,,动点在直线上运动,则的最小值为
A. B. C. D.
【答案】B
【解析】根据题意画出图形,如图所示:
设点关于直线的对称点,
连接,则即为的最小值,
且. 故选.
6.已知点为直线上的动点,当点到和的距离之差最
大时,点坐标为
A. B. C. D.
【答案】C
【解析】如图,作点关于的对称点为,的延长线交于,在l上任取一点,则,则点即为所求.
设关于直线的对称点为,
则,的中点坐标为,
所以,解得,所以.
所以直线的方程为.由,可得.故选D.
二、填空题
7.若点分别为直线与上的动点,则的最小值
为: .
【答案】
【解析】依题意知,两直线平行.所以的最小值为这两条平行直线间的距离,
即.
8.若两条平行直线与之间的距离是,则
.
【答案】
【解析】由题意直线与平行,则,
即且,所以,化为,
所以与之间的的距离为,又,所以,所以.
9.已知点,.点在轴上,且,则的面积为________.
【答案】
【解析】设的中点坐标为,则,
因为,所以的中垂线方程为,即.
令,则,即P点的坐标为,所以,
点P到AB的距离为.
所以.
10.函数的最小值为_________.
【答案】
【解析】,
设,,,
则,
即轴上的一动点到,的距离之和.
作点关于轴的对称点,
连接,则即为距离和的最小值,
,即.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
11.已知直线经过直线与的交点.
(1)若点到的距离为,求的方程;
(2)若直线经过原点,且与直线平行,求与的距离最大值时直线的方程.
【答案】(1)或;(2).
【解析】(1)(解法一)设经过两已知直线交点的直线方程为,
即,所以.即,
所以,解得或.故的方程为或.
(解法二)由,解得交点.
当直线斜率不存在时,方程为:,此时点到的距离为,故符合题意;
当直线斜率存在时,设其方程为:,即,
所以点到的距离为:,解得,
所以直线的方程为:,即.
综上,直线的方程为或.
(2)当两条平行直线,与,两点连线垂直时,两条平行直线间的距离最大.
又,所以两条平行直线的斜率为,
所以直线的方程是,即.
12.已知直线方程为.
(1)证明:直线恒过定点;
(2)当为何值时,点到直线的距离最大,最大值为多少?
(3)若直线分别与轴,轴的负半轴交于两点,求面积的最小值及此时
直线的方程.
【答案】(1)详见解析;(2);
(3)面积的最小值为,此时直线的方程.
【解析】(1)证明:直线方程为,
可化为,
对任意都成立,所以,解得,所以直线恒过定点;
(2)点到直线的距离最大,可知点与定点的连线的距离就是所求最大值,即. 又 ,
且的斜率为,故,解得.
(3)由(1)可知,直线过定点,且分别与轴,轴的负半轴交于两点,
设直线方程为,,分别令,,可得,,
则,
当且仅当时取等号,面积的最小值为. 此时直线的方程.
高中2.3 直线的交点坐标与距离公式授课ppt课件: 这是一份高中2.3 直线的交点坐标与距离公式授课ppt课件,共33页。
高中数学湘教版(2019)选择性必修 第一册2.4 点到直线的距离完整版ppt课件: 这是一份高中数学湘教版(2019)选择性必修 第一册2.4 点到直线的距离完整版ppt课件,共23页。PPT课件主要包含了即时巩固,一求两点间的距离,跟踪训练,B31,还有其他方法吗,两点间的距离公式,课堂小结等内容,欢迎下载使用。
数学选择性必修 第一册2.3 直线的交点坐标与距离公式教课内容课件ppt: 这是一份数学选择性必修 第一册2.3 直线的交点坐标与距离公式教课内容课件ppt,共33页。













