数学必修3第一章 算法初步1.3 中国古代数学中的算法案例教案设计

中国古算名题――孙子问题

山东　　许美文

　　韩信是秦末汉初的著名军事家，据说有一次汉高祖刘邦在卫士的簇拥下来到练兵场，刘邦问韩信有什么办法不要逐个报数，就能知道场上士兵的人数．

　　韩信先令士兵排成了3列纵队进行操练，结果有2人多余；接着他立刻下令将队形改为5列纵列，这一改，又多出3人；随后他又下令改为7列纵队，这一次又剩下2人无法成整行．

　　在场的人都哈哈大知，以为韩信无法清点出准确人数，不料笑声刚落，韩信便高声报告共有士兵2333人．

　　众人听了一愣，不知韩信用了什么办法这么快就能得出正确结果．

　　当然，韩信当时是否这样做，已无从考查，但这个故事却说出一个著名的数学问题，即闻名世界的“孙子问题”．

　　这种神机妙算最早出现在我国《算经十书》之一的《孙子算经》中．其原文是：“今有物不知其数，三三数之剩二，五五数之剩，七七数之剩二．问物几何？” 答曰：“二十三”．意思是说：今有一些事物，不知道它的数目，三个三个地数它们剩余二个，五个五个地数它们剩余三个，七个七个地数它们剩余二个，问这些事物的数目是多少？

　　“孙子问题”相当于求关于的不定方程组的正整数解．

　　《孙子算经》中给出了具体的解法，其步骤是：选定的一个倍数，被3除余1，即70；选定的一个倍数，被5除余1，即70；选定的一个倍数，被5除余1，即21；选定的一个倍数，被7除余1，即15．然后按下式计算．．式中为3，5，7的最小公倍数，为适当的整数，使用，这里取．

　　原题及其解法中的3，5，7后来叫“定母”，70，21，15叫“乘数”．求乘数的方法在《孙子算经》中没有说明，直到1247年南宋数学家秦九韶在《数书九章》中才给出具体求法．分析一下乘数，70是5和7的最小公倍数的2倍，21，15分别是3和7，3和5的最小公倍数的1倍．这些2，1，1，秦九韶称为“乘率”，求出乘率就可以知道“乘数”，《数书九章》中秦九韶详细地论述了推算乘率的方法，称为“大衍求一术”．

　　这种解法后来传入欧洲，欧洲学者发现此解法和高斯的解法本质上是一致的，但比高斯早了500余年．所以，人们将这种问题的通用解法称为“孙子剩余定理”或“中国剩余定理”．

　　求解“孙子问题”的算法很多，下面为同学们介绍一种普通的算法．

　　第一步：；

　　第二步：若除以3余2不成立，则执行第三步；否则，执行第二步；

　　第三步：若除以5余3不成立，则执行第四步；否则，执行第二步；

　　第四步：若除以7余2不成立，则执行第五步；否则，执行第二步；

　　第五点：输出．

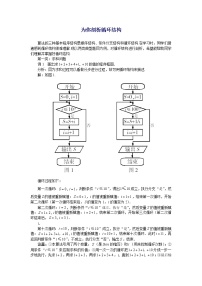
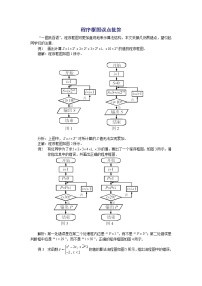
　　其程序框图如下图所示：

　　同学们，你们还能想出求解“孙子问题”的其他算法吗？赶快开动脑筋好好想想吧！