高中数学：1.1《导数与函数的单调性》教案（北师大版选修2-2）

§1   函数的单调性与极值

第一课时  导数与函数的单调性（一）

一、教学目标：1、知识与技能：⑴理解函数单调性的概念；⑵会判断函数的单调性，会求函数的单调区间。2、过程与方法：⑴通过具体实例的分析，经历对函数平均变化率和瞬时变化率的探索过程；⑵通过分析具体实例，经历由平均变化率及渡到瞬时变化率的过程。3、情感、态度与价值观：让学生感悟由具体到抽象，由特殊到一般的思想方法。

二、教学重点：函数单调性的判定   

教学难点：函数单调区间的求法

三、教学方法：探究归纳，讲练结合

四、教学过程

（一）．创设情景

函数是客观描述世界变化规律的重要数学模型，研究函数时，了解函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的．通过研究函数的这些性质，我们可以对数量的变化规律有一个基本的了解．下面，我们运用导数研究函数的性质，从中体会导数在研究函数中的作用．

（二）．新课探究

1．问题：图3.3-1（1），它表示跳水运动

中高度随时间变化的函数的图像，图3.3-1

（2）表示高台跳水运动员的速度随时间

变化的函数的图

像．

运动员从起跳到最高点，以及从最高点到入

水这两段时间的运动状态有什么区别？

通过观察图像，我们可以发现：（1）运动员从起点到最高点，离水面的高度随时间的增加而增加，即是增函数．相应地，．（2）从最高点到入水，运动员离水面的高度随时间的增加而减少，即是减函数．相应地，．

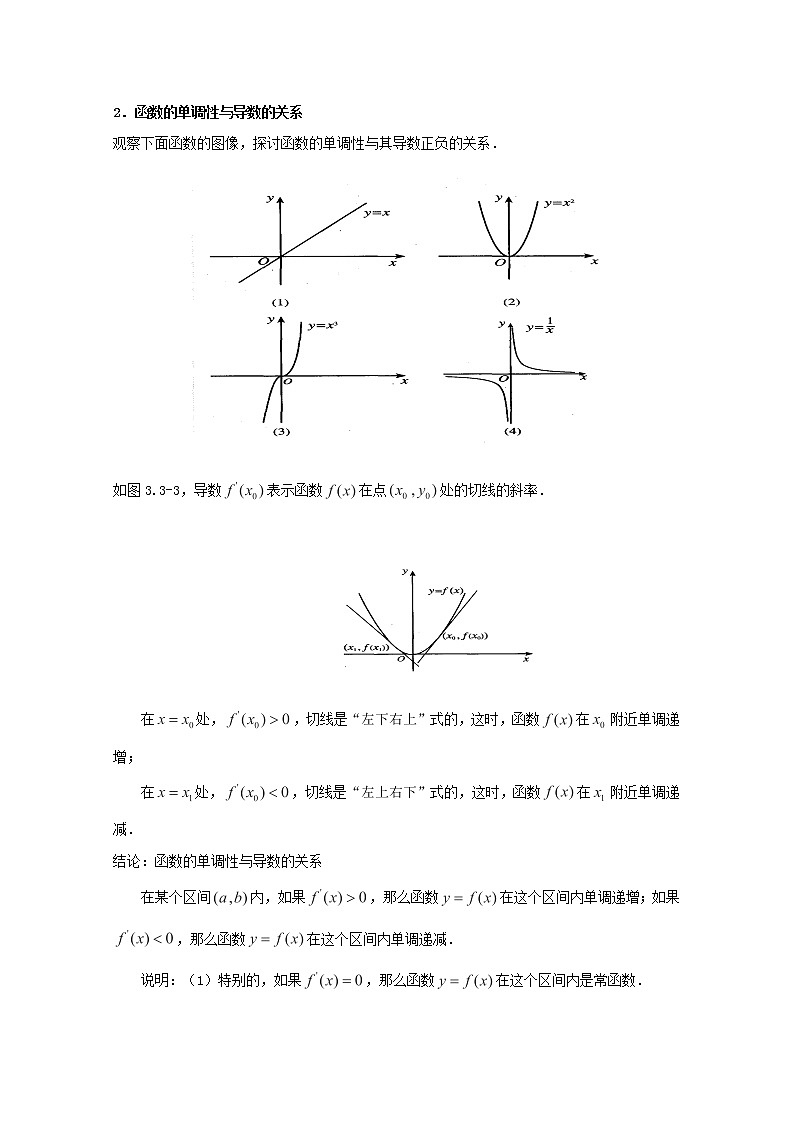
2．函数的单调性与导数的关系

观察下面函数的图像，探讨函数的单调性与其导数正负的关系．

如图3.3-3，导数表示函数在点处的切线的斜率．

在处，，切线是“左下右上”式的，这时，函数在附近单调递增；

在处，，切线是“左上右下”式的，这时，函数在附近单调递减．

结论：函数的单调性与导数的关系

在某个区间内，如果，那么函数在这个区间内单调递增；如果，那么函数在这个区间内单调递减．

说明：（1）特别的，如果，那么函数在这个区间内是常函数．

3．求解函数单调区间的步骤：

（1）确定函数的定义域；（2）求导数；（3）解不等式，解集在定义域内的部分为增区间；（4）解不等式，解集在定义域内的部分为减区间．

（三）．典例探析

例1、已知导函数的下列信息：

当时，；

当，或时，；

当，或时，

试画出函数图像的大致形状．

解：当时，，可知在此区间内单调递增；

当，或时，；可知在此区间内单调递减；

当，或时，，这两点比较特殊，我们把它称为“临界点”．

综上，函数图像的大致形状如图3.3-4所示．

例2、判断下列函数的单调性，并求出单调区间．

（1）；            （2）

（3）；  （4）

解：（1）因为，所以，

因此，在R上单调递增，如图3.3-5（1）所示．

（2）因为，所以，

当，即时，函数单调递增；

当，即时，函数单调递减；

函数的图像如图3.3-5（2）所示．

（3）因为，所以，

因此，函数在单调递减，如图3.3-5（3）所示．

（4）因为，所以              ．

当，即             时，函数            ；

当，即             时，函数            ；

函数的图像如图3.3-5（4）所示．

注：（3）、（4）生练

例3．如图3.3-6，水以常速（即单位时间内注入水的体积相同）注入下面四种底面积相同的容器中，请分别找出与各容器对应的水的高度与时间的函数关系图像．

分析：以容器（2）为例，由于容器上细下粗，所以水以常速注入时，开始阶段高度增加得慢，以后高度增加得越来越快．反映在图像上，（A）符合上述变化情况．同理可知其它三种容器的情况．

    解：

思考：例3表明，通过函数图像，不仅可以看出函数的增减，还可以看出其变化的快慢．结合图像，你能从导数的角度解释变化快慢的情况吗？

  一般的，如果一个函数在某一范围内导数的绝对值较大，那么函数在这个范围内变化的快，这时，函数的图像就比较“陡峭”；反之，函数的图像就“平缓”一些．如图3.3-7所示，函数在或内的图像“陡峭”，在或内的图像“平缓”．

例4、求证：函数在区间内是减函数．

证明：因为

当即时，，所以函数在区间内是减函数．

说明：证明可导函数在内的单调性步骤：（1）求导函数；（2）判断在内的符号；（3）做出结论：为增函数，为减函数．

（四）．课堂练习：课本P59页练习1（1）；2

（五）．回顾总结：（1）函数的单调性与导数的关系；（2）求解函数单调区间；（3）证明可导函数在内的单调性

（六）．布置作业：课本P62页习题3-1A组1、2

五、教后反思：