初中沪科版第4章 直线与角4.5 角的比较与补（余）角教案

4.5 角的比较与补（余）角教案

一、教学目标：

   知识与技能：1.会比较两个角的大小，能够结合图形实际将一个角写成两个角的和、差的形式；

               2.了解角平分线的意义，并能够用符号语言表示.

   过程与方法：1.通过学生熟悉的数学知识导入，互相交流探究，发现比较角的大小的三种方法，通过对探究的新知识尝试应用，进一步学习几何语言说理的数学方法；

              2.了解简单的推理论证的思想：“问题－分析－说理”的分析几何问题的方法.

   情感、态度与价值观：在操作、观察、思考、发现的过程中，体会学习几何知识的思想方法，培养学生之间的合作意识与探究精神.

二、教学重难点：

  教学重点：两个角大小的比较方法.

  教学难点：用几何语言进行简单的说理.

三、教学过程：

（一）创设情境，引入新知

操作：幻灯片展示足球运动员射门图片。

思考1：你知道运动员从哪个位置射门射进球的可能性更大吗？

思考2：如果是你，你会选择哪个位置射门？

（二）合作交流，探索新知

观察：把∠DEF移动，使它的顶点E移到和∠ABC的顶点B重合，一边ED和BA重合，另一边EF和BC落

在BA的同旁.（①顶点重合；②一边重合；③另一边在同旁），请认真观察下面的演示，分别说出角的大

小.

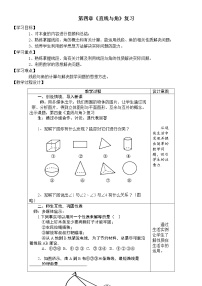
观察图形，你能得出什么结论？

（1）如果EF和BC重合，那么∠DEF＝ ∠ABC；

（2）如果EF落在∠ABC内部，那么∠DEF﹤ ∠ABC；

（3）如果EF落在∠ABC外部，那么∠DEF ﹥∠ABC.

观察：下面图形中有多少个角？请写出来.除了我们能比较它们的大小关系外，还发现它们还有什么数量

关系？

（三）合作交流，应用新知

例1 如图，求解下列问题：

（1）比较∠AOC 与∠BOC， ∠BOD与∠COD的大小；

（2）将∠AOC写成两个角的和与两个角的差的形式.

（四）合作交流，再探新知

操作：在角的内部，以角的顶点为端点的一条射线把这个角分成两个相等的角，这条射线叫做这个角的平

分线.请尝试画出符合要求的几何图形.

结合角平分线定义和图形，请尝试写成几何符号语言形式.

（五）小试牛刀，再用新知

例2 如图，已知OC平分∠BOD， ∠AOD＝1100， ∠COD=350，求∠AOB， ∠AOC的度数.

例3 如图， ∠ COB＝2 ∠ AOC，OD平分

∠ AOB，且∠ COD＝190，求∠ AOB的度数.

（教材151页第5题）

（六）随堂练习，巩固新知

1、教材149页第1题.

2、将第1题改为：

按下列要求画图，并解答问题：

（1）画∠ AOB＝900；

（2）再画∠BOC＝300；

（3）求∠ AOC的度数.

3、如图， ∠ AOB＝ ∠ BOC

＝∠ COD ＝∠ DOE，请写出图中所有的角平分线.

（七）师生互动，小结新知

一、比较角的大小两种方法：叠合法（顶点重合；一边重合；另一边在同旁）和度量法；

二、角的和、差；

三、角平分线；

四、注意几何问题的表达方式：文字语言、几何图形和几何符号语言之间的联系与转化；

五、应用这些知识解答问题.

（八）布置作业，深化新知

教材150页习题4.5第1、2、3、4题；