华师大版七年级下册9.3 用正多边形铺设地面综合与测试图片ppt课件

这是一份华师大版七年级下册9.3 用正多边形铺设地面综合与测试图片ppt课件，共30页。PPT课件主要包含了什么是正多边形等内容，欢迎下载使用。

观察图中的多边形，他们的边、角有什么特点？
正多边形的定义： 各边都相等，各内角也都相等的多边形叫做正多边形。 如图中的多边形分别为：正三角形、正四边形(即正方形)、正五边形、正六边形、正八边形.
正n边形的每个内角为：
你能归纳一下，正多边形的内角度数是怎么算的吗？
正三角形、正四边形（正方形）、正五边形、正六边形、正八边形的内角分别是多少度？
正n边形的每个外角为：
2.用相同的正多边形如何密铺？
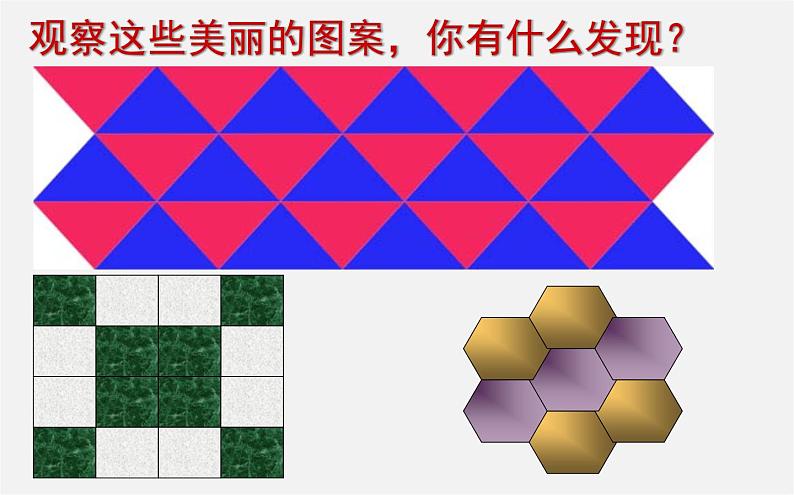
观察这些美丽的图案，你有什么发现？
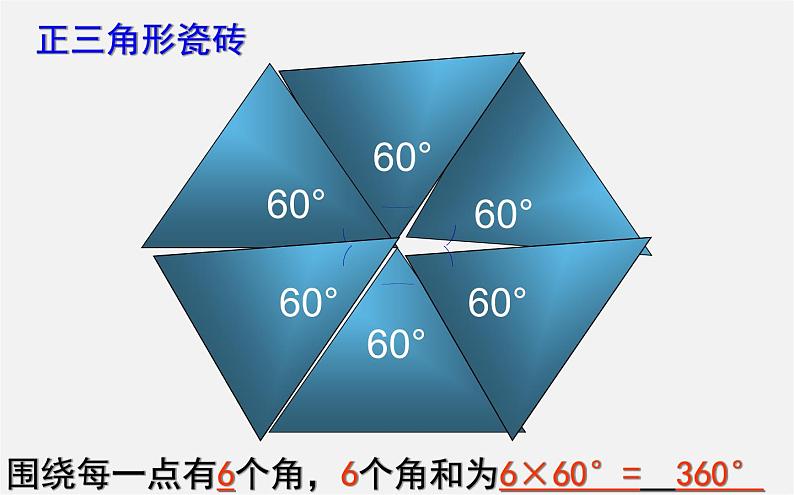
围绕每一点有6个角，6个角和为6×60°= 360°
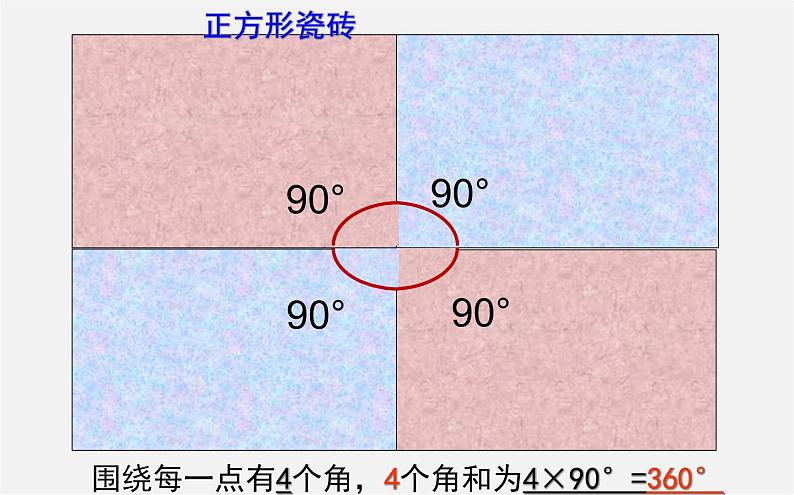
围绕每一点有4个角，4个角和为4×90°=360°
围绕每一点有3个角，3个角和为3×108°= 324°
围绕每一点有3个角，3个角和为3×120°=360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7≈128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
为什么有的正多边形能铺满地面，有的却不行呢？
规律： 使用给定的某种正多边形，当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时，就能铺满地面。
探究 ：n只能是哪些数？　　
能用同一种正多边形拼地板的正多边形只有
正三角形、正方形、正六边形．
4.用两种正多边形 能密铺吗？
如图：把相邻两行正三角形分开，添一行正方形，得到下面的图。它表明把正三角形和正方形结合在一起也能铺满地面。为什么？
解： 3×60°+2 ×90°=360° 答：能铺满地面。
分析：因为正三角形的内角为60度，正方形的内角为90度，这样用3块正三角形和2块正方形，他们的内角和为一个周角360度，所以能铺满地面。
为什么以下几组图形能够如此巧妙的结合在一起？
1.正八边形和正方形组合。
2.正十二边形和正三角形组合。
正十二边形和正三角形组合。
规律：当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时，就能铺满地面。
5.用三种正多边形 能密铺吗？
正十二边形、正六边形和正方形的组合。
1、能密铺的条件是什么？
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时，就能铺满地面。
2、能用同一种正多边形拼地板的正多边形有哪些？
能用同一种正多边形拼地板的正多边形只有正三角形、正方形、正六边形．
围绕一点能拼成360º，但能扩展到整个平面，即铺满地面吗？
尽管能围绕一点拼成360º，但不能扩展到整个平面。
规律：当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时，就能铺满地面。
注：有时几种正多边形的组合能围绕一点拼成 周角，但不能扩展到整个平面，即不能铺 满平面。如：正五边形与正十边形的组合。