2021-2022学年人教版九年级数学上册期中复习检测试卷（Word版含答案）

这是一份2021-2022学年人教版九年级数学上册期中复习检测试卷（Word版含答案），共14页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

学校:___________姓名：___________班级：___________考号：___________
一、选择题（本大题共10小题，共30分）
下列图形中，是轴对称图形，但不是中心对称图形的是( )
A. B.
C. D.
已知y=(m-2)xm2−2+2m是关于x的二次函数，则下列说法正确的是( )
A. 有最大值4B. 有最大值−4C. 有最小值4D. 有最小值−4
在平面直角坐标系中,将点(-2,3)关于原点对称的点向左平移2个单位长度得到的点的坐标是（ ）
A. (4,−3)B. (−4,3)C. (0,−3)D. (0,3)
用公式法解方程4y2=12y+3,解为（ ）
A. y=−3±62B. y=3±62C. y=3±232D. y=−3±232
若x=-2是关于x的方程ax2+bx+8=0的一个根，则5-2a+b的值是( )
A. 13B. 9C. 1D. −3
已知抛物线y=x2-8x+c的顶点在x轴上,则c的值是（ ）
A. 16B. −4C. 4D. 8
已知关于x的一元二次方程(k-1)x2-2x+2=0有两个不相等的实数根,则k的取值范围是（ ）
A. k<32B. k≤32C. k<32且k≠1D. k≤32且k≠1
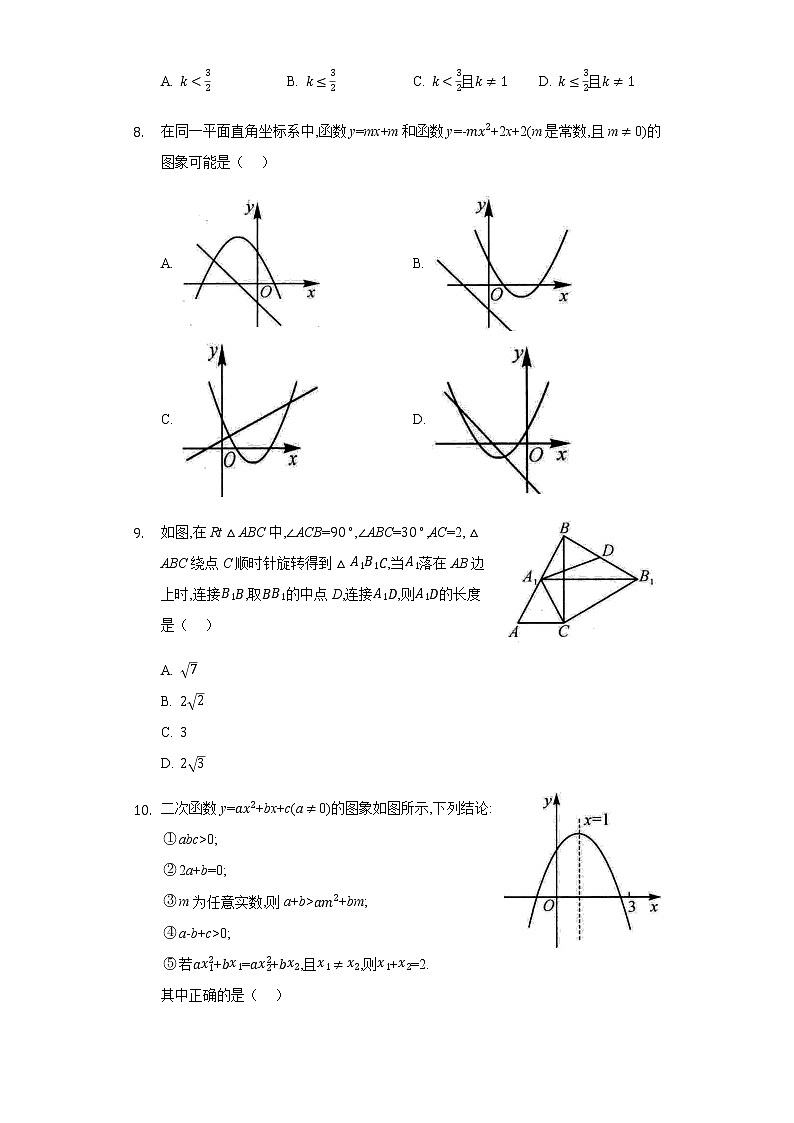
在同一平面直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是（ ）
A. B.
C. D.
如图,在Rt△ABC中,∠ACB=90∘,∠ABC=30∘,AC=2,△ABC绕点C顺时针旋转得到△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是（ ）
A. 7
B. 22
C. 3
D. 23
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
abc>0;
2a+b=0;
m为任意实数,则a+b>am2+bm;
a-b+c>0;
若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.
其中正确的是（ ）
A. ① ② ③
B. ② ④
C. ② ⑤
D. ② ③ ⑤
二、填空题（本大题共8小题，共24分）
方程x2=x的根是 .
如图所示,在下列四组图形中,右边图形与左边图形成中心对称的有 .
已知方程3x2-4x-2=0的两个根是x1,x2,则1x1+1x2= .
某楼盘2018年房价为每平方米8100元,经过两年连续降价后,2020年房价为每平方米7600元.设该楼盘这两年房价平均下降率为x,根据题意可列方程为 .
已知点P在抛物线y=(x−2)2上,设点P的坐标为(x,y),当0≤x≤3时,y的取值范围是 .
如图,若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时抛物线位于x轴下方的图象对应的x的取值范围是 .
如图,在边长为1的正方形网格中,A(1,7),B(5,5),C(7,5),D(5,1).若线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一定角度可以得到另一条线段,则这个旋转中心的坐标为 .
运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:足球距离地面的最大高度为20 m;足球飞行路线的对称轴是直线t=92;足球被踢出9.5 s后落地;足球被踢出7.5 s时,距离地面的高度是11.25 m.其中不正确的结论是 .
三、计算题（本大题共1小题，共6分）
解方程:
(1)2x2+3=7x. (2)(2x+1)2+4(2x+1)+3=0.
四、解答题（本大题共6小题，共60分）
如图,在平面直角坐标系中,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0).
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1.
(2)画出将△ABC绕原点O顺时针方向旋转90∘得到的△A2B2O.
如图,将矩形ABCD绕点A顺时针旋转得到矩形AEFG,点E在BD上.
(1)求证:FD=AB.
(2)连接AF,求证:∠DAF=∠EFA.
已知关于x的一元二次方程x2-2x+m-1=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)当x12+x22=6x1x2时,求m的值.
某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25 m),另外三边用木栏围成,木栏长40 m.
(1)若养鸡场的面积为200m2,求养鸡场平行于墙的一边长.
(2)养鸡场的面积能达到250m2吗?如果能,请给出设计方案;如果不能,请说明理由.
服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围.
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
如图(a)，抛物线y=-x2+bx+c过点A(-1，0)、点B(3，0)，与y轴交于点C.在x轴上有一动点E(m，0)（0< m<3），过点E作直线l⊥x轴，交抛物线于点M.
(1)求抛物线的解析式及C点坐标；
(2)当m=1时，D是直线l上的点且在第一象限内，若△ACD是以∠DCA为底角的等腰三角形，求点D的坐标；
(3)如图(b)，连接BM并延长交y轴于点N，连接AM，OM，设△AEM的面积为S1，△MON的面积为S2，若S1=2S2，求m的值.
参考答案
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】A
10.【答案】C
11.【答案】x1=0,x2=1
12.【答案】​​​​​​​
13.【答案】-2
14.【答案】8100(1−x)2=7600
15.【答案】0≤y≤4
16.【答案】0< x<2
17.【答案】(3,3)或(6,6)
18.【答案】​​​​​​​
19.【答案】解:(1)x1=12,x2=3.
​​​​​​​(2)x1=-1,x2=-2.
20.【答案】解:(1)如图所示,即为所求;
(2)如图所示,即为所求.
21.【答案】证明:(1)由旋转的性质,得AE=AB,∠AEF=∠ABC=∠DAB=90∘,EF=BC=AD,
∴∠AEB=∠ABE.
又∵∠ABE+∠EDA=90∘=∠AEB+∠DEF,
∴∠EDA=∠DEF.
又∵DE=ED,
∴△AED≌△FDE(SAS).
∴AE=FD.
又∵AE=AB=CD,
∴FD=AB.
(2)设EF与AD的交点为点H.
∵∠EDA=∠DEF,
∴HE=HD.
又∵EF=AD,
∴EF-HE=AD-HD,即HF=HA.
∴∠DAF=∠EFA.
22.【答案】解:(1)∵原方程有两个实数根,
∴Δ​​​​​​​=(−2)2-4(m-1)≥0,即4-4m+4≥0.
解得m≤2.
(2)∵x1+x2=2,x1x2=m-1,且x12+x22=6x1x2,
∴(x1+x2)2-2x1x2=6x1x2,即(x1+x2)2-8x1x2=0.
∴22-8(m-1)=0.
∴m=32.
∵m=32<2,
​​​​​​​∴符合条件的m的值为32.
23.【答案】解:(1)养鸡场平行于墙的一边长为20 m.
(2)不能.
​​​​​​​理由如下:
根据题意,得x(40-2x)=250,
∴-2x2+40x-250=0.
∵Δ=402-4×(-2)×(-250)=-400<0,
∴方程无实数根.
​​​​​​​∴不能使养鸡场的面积达到250m2.
24.【答案】解:(1)当10≤x≤50时,设y与x之间的函数关系式为y=kx+b,
则10k+b=100,50k+b=80.
解得k=−0.5,b=105.
∴当10≤x≤50时,y与x之间的函数关系式为y=-0.5x+105.
当x>50时,y=80,
∴y与x之间的函数关系式为y=−0.5x+105(10⩽x⩽50)80(x>50).
(2)批发该种服装40件时,服装厂获得利润最大,最大利润是800元.
25.【答案】解：(1)把点A(-1，0)，点B(3，0)代入y=-x2+bx+c，得
−1−b+c=0−9+3b+c=0，解得b=2c=3，
∴抛物线的解析式为y=-x2+2x+3.
把x=0代入y=-x2+2x+3，得y=3，
∴C(0，3).
(2)当m=1时，点D的横坐标为1.
设D(1，a)，
本题有两种情况：当∠DCA=∠CDA时，AC=AD，
∴12+32=22+a2，解得a=±6.
∵D在第一象限，
∴a>0，
∴a=6，
∴D(1，6)；
当∠DCA=∠DAC时，AD=CD，
∴22+a2=(1−0)2+(3−a)2，
解得a=1，
∴D(1，1).
综上所述，点D的坐标为(1，6)或(1，1).
(3)由题意，得M(m，-m2+2m+3)，
设直线BM的解析式为y=kx+h，则
mk+ℎ=−m2+2m+33k+ℎ=0，
解得h=3(−m2+2m+3)3−m，即ON=3(−m2+2m+3)3−m.
∵S1=12AE⋅ME=12(m+1)(-m2+2m+3)，
S2=12ON⋅OE=12m⋅3(−m2+2m+3)3−m，
S1=2S2，
∴12(m+1)(-m2+2m+3)=2×12m⋅3(−m2+2m+3)3−m，
整理得(m2+4m-3)(-m2+2m+3)=0，
又0< m <3时，- m2+2m+3>0，
∴ m2+4m-3=0，
解得m1=-2+7，m2=-2-7，
经检验，m1=-2+7，m2=-2-7都是原方程的解.
∵0< m <3，
​​​​​​​∴ m2=-2- 7不合题意，舍去.
∴m=-2+7.
t/s
0
1
2
3
4
5
6
7
⋯
h/m
0
8
14
18
20
20
18
14
⋯