冀教版八年级下册22.4 矩形教学演示课件ppt

这是一份冀教版八年级下册22.4 矩形教学演示课件ppt，共20页。PPT课件主要包含了几何画板，矩形的定义及性质，一个角是直角，例1练习小结，四个角都是直角，对边平行且相等，互相平分且相等，是轴对称图形，课堂练习等内容，欢迎下载使用。
什么叫平行四边形？它和四边形有什么区别？
我们已经知道平行四边形是特殊的四边形，因此平行四边形除具有四边形的性质外，还有它的特殊性质，同样对于平行四边形来说，也有特殊情况即特殊的平行四边形，这堂课我们就来研究一种恃殊的平行四边形——矩形
日常生活中常见的矩形。
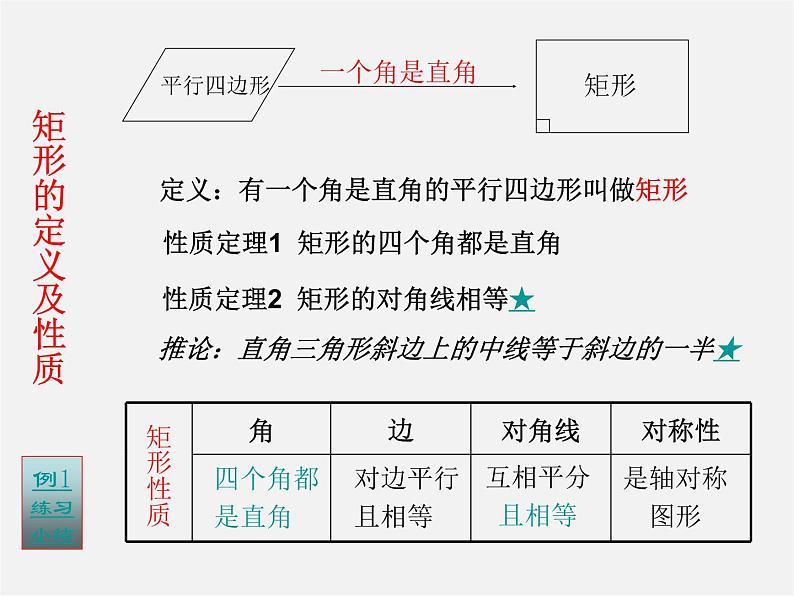
定义：有一个角是直角的平行四边形叫做矩形
性质定理1 矩形的四个角都是直角
性质定理2 矩形的对角线相等★
推论：直角三角形斜边上的中线等于斜边的一半★
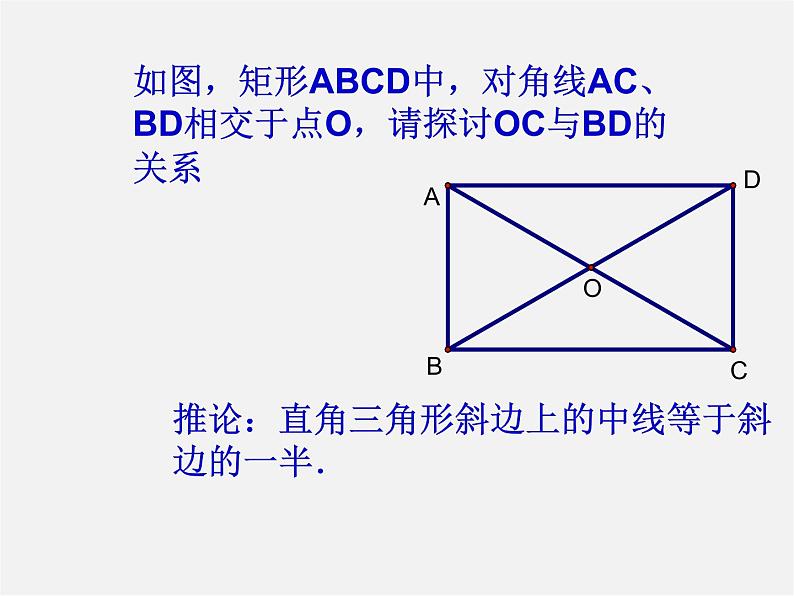
推论：直角三角形斜边上的中线等于斜边的一半．
如图，矩形ABCD中，对角线AC、BD相交于点O，请探讨OC与BD的关系
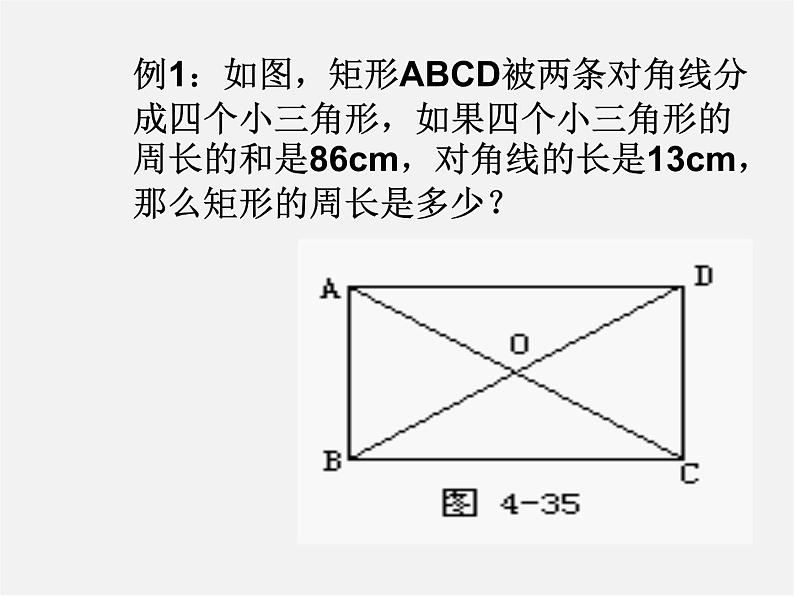
例1：如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm，对角线的长是13cm，那么矩形的周长是多少？
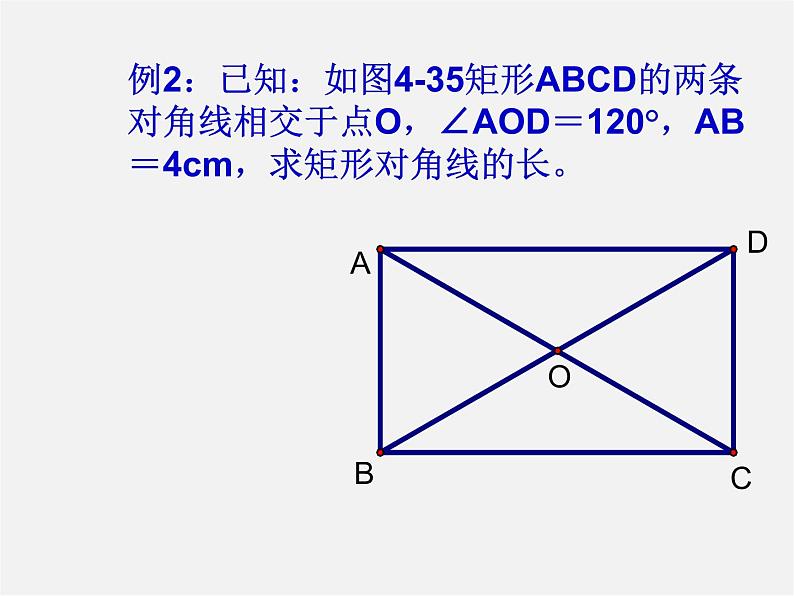
例2：已知：如图4-35矩形ABCD的两条对角线相交于点O，∠AOD＝120°，AB＝4cm，求矩形对角线的长。
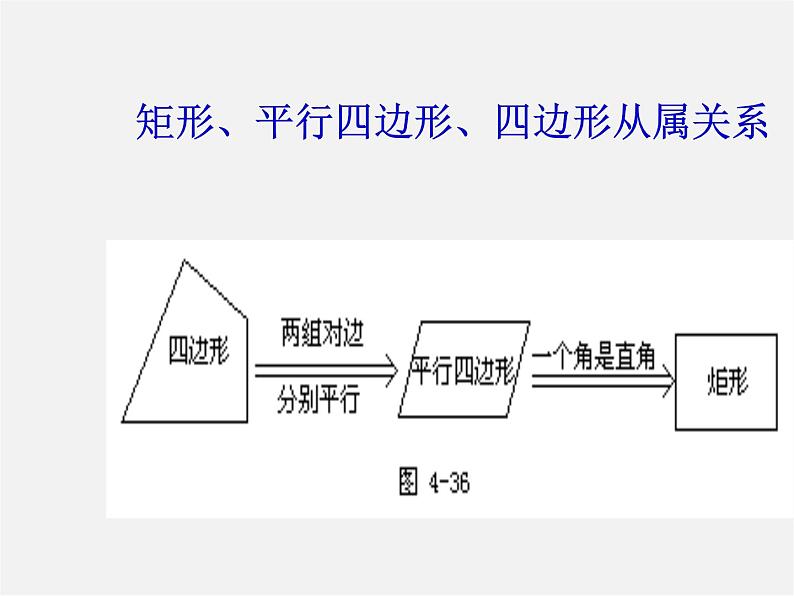
矩形、平行四边形、四边形从属关系
（2）如图，在矩形ABCD中，AC与BD相交于点O，AB=3cmBC=4cm,AC=5cm，则AO= cm,BO= cm.
（3）如图，在矩形ABCD中，AO CO BO DO,所以在直角三角形ABC中，AO CO BO，即直角三角形中，斜边上的中线等于斜边的 。
（4）矩形具有而平行四边形不具有的性质（ ）（A）内角和是360度（B）对角相等（C）对边平行且相等（D）对角线相等
（5）下面性质中，矩形不一定具有的是（ ）（A）对角线相等（B）四个角相等（C）是轴对称图形（D）对角线垂直
6）下面图形中，既是轴对称图形，又是中心对称图形的是（ ）（A）角（B）任意三角形（C）矩形（D）等腰三角形
（7）由已知矩形的一个顶点向其所对的对角线引垂线，该垂线分直角为3：1两部分，则垂线与另一条对角线的夹角是（ ）（A）60度（B）45度（C）30度（D）22.5度
（8）矩形两条对角线的夹角是120度，短边长为4cm。求矩形的对角线长。
（9）如图，已知平行四边形ABCD的对角线AC、BD相交于点O，三角形AOB是等边三角形，AB=4cm。平行四边形ABCD是矩形吗？说说你的理由。
（10）任意剪一个平行四边形的纸片（如图），过一个顶点作出它的一条垂线段h，沿这条垂线段剪下这个三角形纸片，将它平移到右边的位置，平移距离等于平行四边形的底边长a。 (a)    所得得图形是怎样的四边形？为什么？ (b)求原平行四边形的面积。
（11）如图，矩形ABCD的对角线AC、BD相交于点O，若AC=1.8cm,试求AB的长。
已知：矩形ABCD 求证：AC = BD
证明：在矩形ABCD中∵∠ABC = ∠DCB = 90° （ ）AB = DC ， BC = CB∴△ABC≌△DCB ∴AC = BD
推论：直角三角形斜边上的中线等于斜边的一半
证明：延长CD到E使DE=CD，连结AE、BE.
∵AD = BD ，CD = ED∴ACBE是平行四边形
例1 已知：矩形ABCD的两条对角线相交与O，∠AOD=120°，AB = 4cm. 求矩形对角线的长
解：∵四边形ABCD是矩形 ∴OA = OD（ ） ∵ ∠AOD=120° ∴ ∠1=30° 又∵ ∠ABC=90°（ ） ∴BD = 2AB=2×4=8cm
　2. 过四边形的各个顶点分别作对角线的平行线，若这四 条平行线围成一个矩形，则原四边形一定是