数学16.2 二次根式的运算教案

这是一份数学16.2 二次根式的运算教案，共4页。
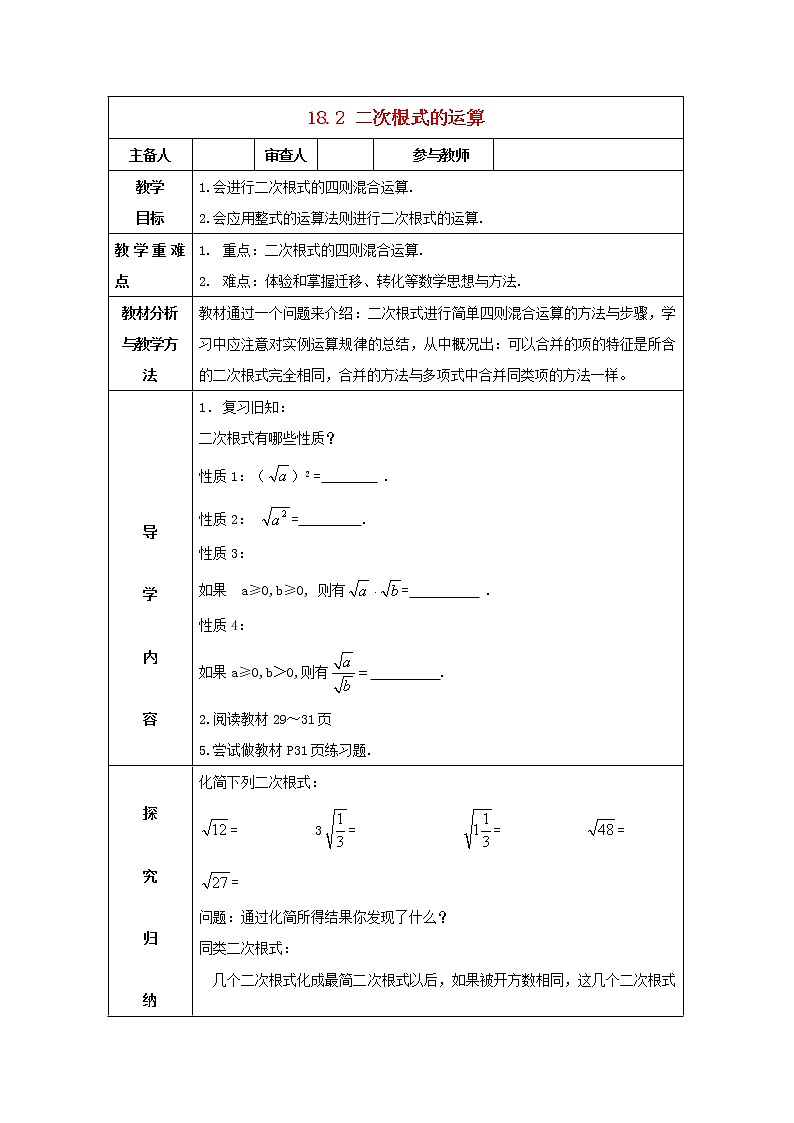
18.2 二次根式的运算 主备人 审查人 参与教师 教学目标1.会进行二次根式的四则混合运算.2.会应用整式的运算法则进行二次根式的运算.教学重难点重点：二次根式的四则混合运算.难点：体验和掌握迁移、转化等数学思想与方法.教材分析与教学方法教材通过一个问题来介绍：二次根式进行简单四则混合运算的方法与步骤，学习中应注意对实例运算规律的总结，从中概况出：可以合并的项的特征是所含的二次根式完全相同，合并的方法与多项式中合并同类项的方法一样。    导 学 内 容 1．  复习旧知：二次根式有哪些性质？性质1：（）2 =         .性质2： =         .性质3：如果  a≥0,b≥0, 则有=           .性质4：如果a≥0,b＞0,则有          .2.阅读教材29～31页               5.尝试做教材P31页练习题. 探 究 归 纳化简下列二次根式：=           3=               =            ==问题：通过化简所得结果你发现了什么？同类二次根式：  几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式.如、3 、  、  、化成最简二次根式以后所得结果中都是与一个有理数的乘积，所以它们就是同类二次根式. 问题：△ABC中，∠C=900，AB=cm, BC=cm, 求△ABC的周长l.解  注意：在进行二次根式相加减时，先把各个二次根式化成最简二次根式，再把同类二次根式进行合并，合并方法与合并同类项类似。在同类二次根式的运算中，实数的运算性质和法则同样适用。        例 题 讲 解例6 计算：（1） 2        （2） （解 解 （3）解   例7      计算：（1）          （2） （2＞0，y＞0）解 解   巩固提高计算:(1)        (2)      ( 3)解 解 解 (4) (解   2.化简:(1)         (2) 解 解     下列根式中,哪些是最简二次根式?  , ,  ,  .     教 学 反 思