






沪科版七年级下册6.2 实数备课ppt课件
展开1、平方根: ①若 ,则 称为 的平方根, 即: 是被开方数,根指数是2,可以省略。 ② 正数有两个平方根,它们互为相反数,0的 平方根是0,负数没有平方根。 ③正平方根: ,它是一个非负数
n次方根中,偶次方根概念可由平方根推广而得。
【例1】0.16的平方根是 ; 的算术平方根是 ;
【例2】已知 , 化简 .
【例3】一个数等于其倒数的4倍,该数为_____.
【例4】 的平方根是________, 的平方根是________.
1、判断:64的平方根是8, 8是64的平方根。
2、平方根等于本身的数有( ),正平方根等于本身的数有( )。
3、0.04的平方根表示为( ),值为( ),正平方根表示为( ),值为( )。
2、写出大于 且小于 的所有整数。
3、 的相反数是 ;绝对值是 。
4、在数轴上表示 的点与表示 的距离是?
5、写出下列各数的整数部分和小数部分
7、化简: = .
3、立方根: ①若 ,则 称为是 的立方根, 即: ②一个正数有一个正立方根,一个负数有一个负立方根,0的立方根是0 ③恒等式:
n次方根中,奇次方根概念可由立方根推广而得
1、求下列各数的立方根:
3、若 ,则 的值是?
4、把一个棱长为 的立方体金属块切割成体积相 等的两部分,然后把每一部分锻造成小立方体金属块,求这小立方体金属块的棱长。
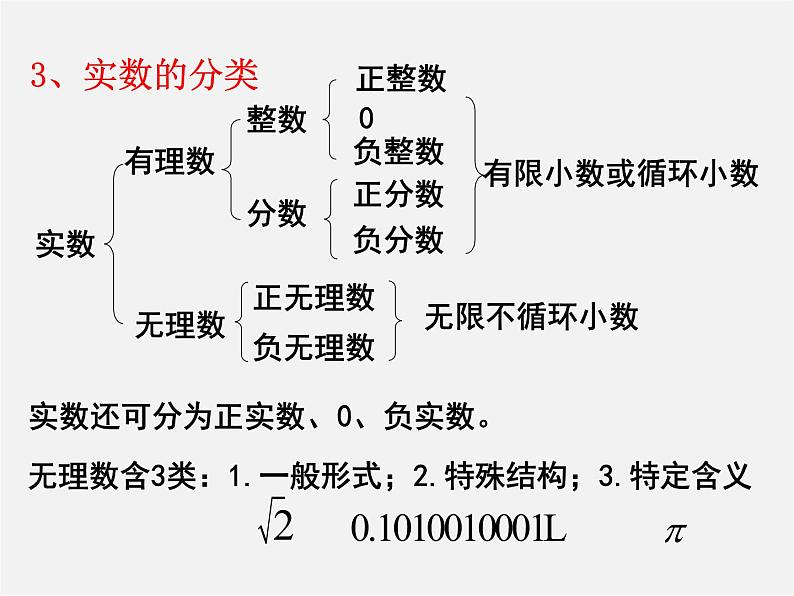
实数还可分为正实数、0、负实数。
无理数含3类:1.一般形式;2.特殊结构;3.特定含义
4、实数的运算:实数的运算法则:先算乘方和开方,再算乘和除,最后算加和减,有括号的先算括号里的。
(1)任何非负数的和仍是非负数;(2)若几个非负数的和是0,那么这几个非负数均为0.
【例1】若 , 则 .
【例2】若 与 互为相反数, 则 的值为 。
数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
【例1】用“<”或“>”填空: ___ , ___
【例4】求下列各式中的x
【例1】写出两个大于1小于4的无理数____、____.
【例2】 的整数部分为____.小数部分为_____
【例3】一个立方体的棱长是4㎝,另一个立方体的体积是它的8倍,则所做的立方体的表面积是_______.
1. (x-1)2=64 2.
A 无限小数是无理数 B 绝对值等于本身的数是正数C 实数和数轴上的点一一对应D 带根号的数是无理数
【例5】下列叙述正确的是( )
【例6】下列说法中,错误的个数是 ( )
①无理数都是无限小数;②无理数都是开方开不尽的数;③带根号的都是无理数;④无限小数都是无理数。
A.1个 B.2个 C.3个 D.4个
【例7】数轴上的点与( )一一对应.
A.整数 B.有理数 C.无理数 D.实数
【例8】相反数是本身的数是 ;绝对值是本身的数 是 ;倒数是本身的数是 .
【例9】a、b互为相反数,c与d互为倒数, 则a+1+b+cd= .
【例10】 的绝对值为__________.
【例11】找规律,并用公式表示出来.
如图,数轴上表示1、 的对应点分别为A、B,点B关于点A的对称点为C,则点C所表示的数是( )
若 ,则± = 。
你学到了什么?还有什么问题?
初中数学沪科版七年级下册6.2 实数背景图课件ppt: 这是一份初中数学沪科版七年级下册6.2 实数背景图课件ppt,共17页。PPT课件主要包含了它本身,它的相反数,实数大小的比较法则,”号把它们连结起来,课堂作业,求下列各数的绝对值等内容,欢迎下载使用。
沪科版七年级下册6.2 实数教案配套课件ppt: 这是一份沪科版七年级下册6.2 实数教案配套课件ppt,共20页。PPT课件主要包含了知识回顾,学习新知,试一试,做一做,挑战自己,有理数,无理数等内容,欢迎下载使用。
数学沪科版第6章 实数6.2 实数教学ppt课件: 这是一份数学沪科版第6章 实数6.2 实数教学ppt课件,共15页。PPT课件主要包含了有理数,无理数,正有理数,负有理数,正无理数,负无理数,或有理数,无限不循环小数,正实数,负实数等内容,欢迎下载使用。













