


2020-2021学年2.4 线段的垂直平分线备课ppt课件
展开线段的垂直平分线(1)
1.结合具体例子认识什么是线段的垂直 平分线,理解线段的垂直平分线所满 足的两个条件.
2.探索掌握线段垂直平分线的性质定理及 其逆定理.
3.能应用线段垂直平分线的性质定理找出 线段相等.
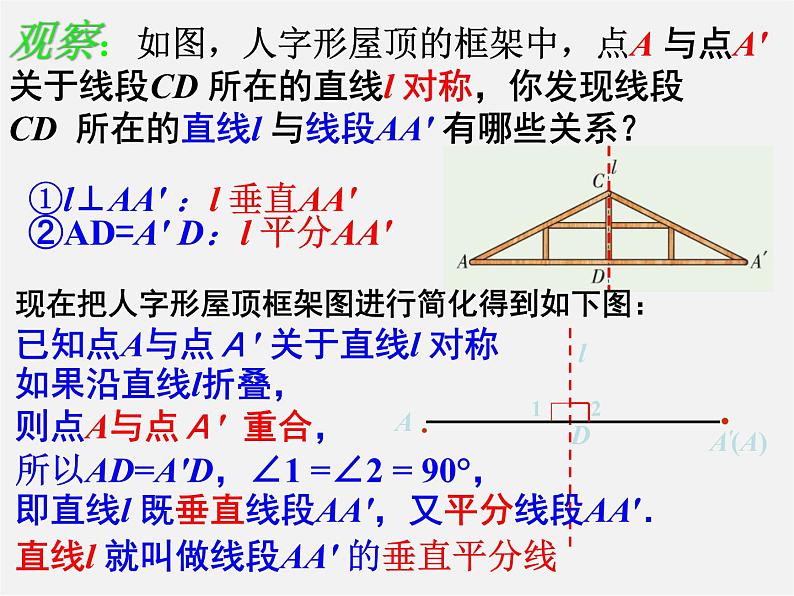
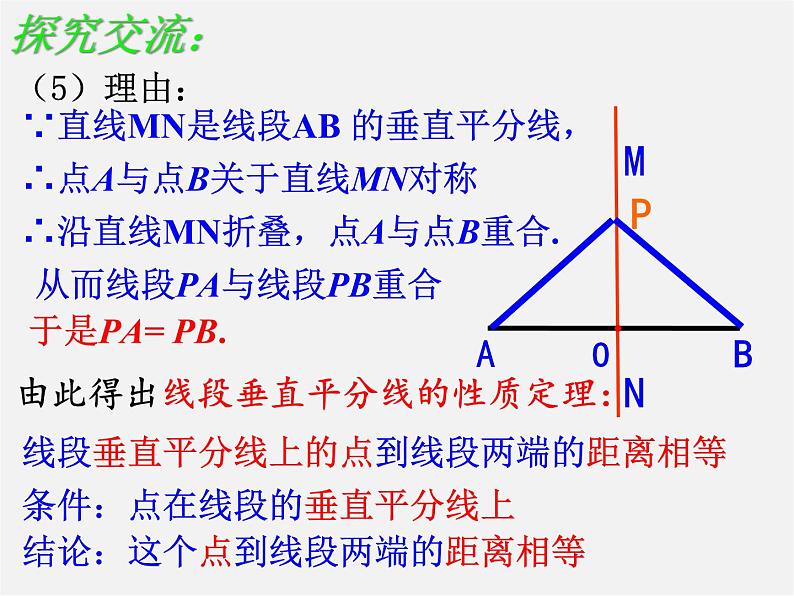
观察:如图,人字形屋顶的框架中,点A 与点A′关于线段CD 所在的直线l 对称,你发现线段CD 所在的直线l 与线段AA′ 有哪些关系?
已知点A与点A′ 关于直线l 对称
现在把人字形屋顶框架图进行简化得到如下图:
①l⊥AA′ :l 垂直AA′
②AD=A′ D:l 平分AA′
如果沿直线l折叠,则点A与点A′ 重合,
所以AD=A′D,∠1 =∠2 = 90°,
即直线l 既垂直线段AA′,又平分线段AA′.
直线l 就叫做线段AA′ 的垂直平分线
________且_______一条线段的直线叫作这条线段的垂直平分线.
想一想:线段是轴对称图形吗? 它的对称轴是什么?
由上得到线段的垂直平分线的定义:
∵_______,_______∴直线l 是线段AA′ 的垂直平分线
线段是轴对称图形, 线段的垂直平分线是它的对称轴.
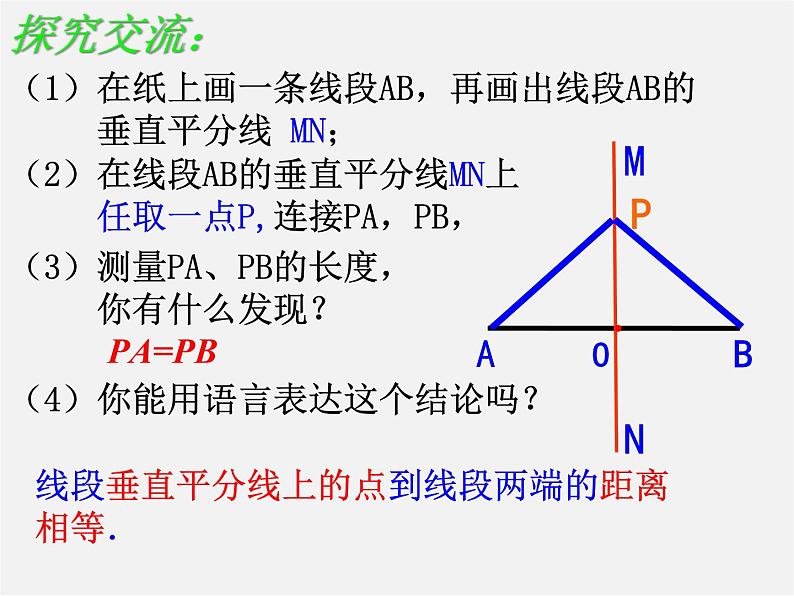
(1)在纸上画一条线段AB,再画出线段AB的 垂直平分线 MN;
(2)在线段AB的垂直平分线MN上 任取一点P,连接PA,PB,
(3)测量PA、PB的长度, 你有什么发现?
线段垂直平分线上的点到线段两端的距离相等.
(4)你能用语言表达这个结论吗?
线段垂直平分线上的点到线段两端的距离相等
∵直线MN是线段AB 的垂直平分线,
∴沿直线MN折叠,点A与点B重合.
∴点A与点B关于直线MN对称
从而线段PA与线段PB重合
由此得出线段垂直平分线的性质定理:
条件:点在线段的垂直平分线上
结论:这个点到线段两端的距离相等
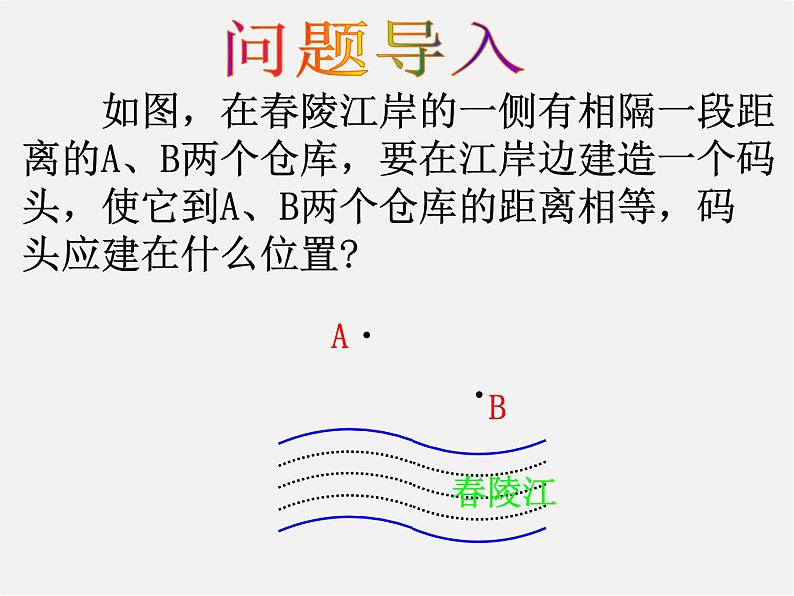
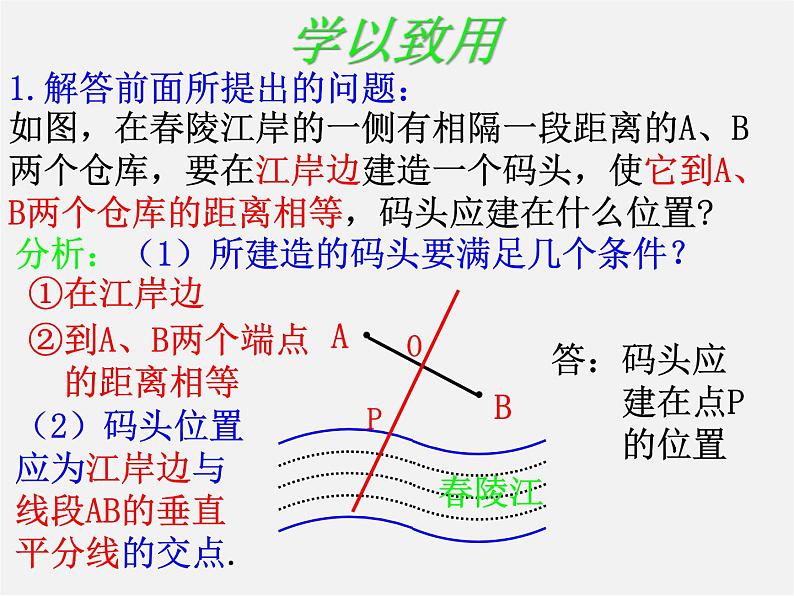
如图,在春陵江岸的一侧有相隔一段距离的A、B两个仓库,要在江岸边建造一个码头,使它到A、B两个仓库的距离相等,码头应建在什么位置?
1.解答前面所提出的问题:
分析:(1)所建造的码头要满足几个条件?
②到A、B两个端点 的距离相等
(2)码头位置应为江岸边与线段AB的垂直平分线的交点.
答:码头应 建在点P 的位置
2.如图,△ABC中,AB=9cm,AC=15cm,BC的 垂直平分线DE交AC于点D,交BC于点E, 求△ABD的周长
∵ DE是BC的垂直平分线
∴ △ABD的周长 =AB+BD+AD
=9+15=24(cm)
方法小结:应用线段的垂直平分线性质定理可帮助我们找到线段相等关系,即线段垂直平分线上的点到这条线段两个端点的距离相等.
(线段垂直平分线上的点到线段两端的距离相等)
3.如图,△ABC中,AB=AC,∠A=36°,AC的 垂直平分线交AB于E,D为垂足,连接EC. (1)求∠ECD的度数;(2)若CE=5,求BC长.
∵ DE是AC的垂直平分线
∴ ∠ECD=∠A=36°
∵AB=AC ∠A=36°
又∵∠BEC=∠A+∠ECA=72°
∴ BC = EC =5
(1)如图,在△ABC中,AB的垂直平分线 分别交AB,BC于点D,E,∠B=30°, ∠BAC= 80°, 求∠CAE的度数.
∵ DE是AB的垂直平分线
∴ ∠BAE=∠B=30°
又∵∠CAE+∠BAE=∠BAC
∴ ∠CAE=∠BAC-∠BAE
=80°-30°=50°
(2)如图,在△ABC中,AB< AC,BC边上的 垂直平分线DE交BC于点E,AC=15cm, ΔABD的周长是24cm,求AB的长.
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( ) B.8cm C.10cm D.12cm
∵DE是AB的垂直平分线,∴AE=BE(线段垂直平分线上的点到线段两端的距离相等).又∵在△BCE中,BE+CE+BC=18cm,BC=8cm,∴BE+CE=10cm.∴AC=AE+CE=BE+CE=10cm. 故应选择C.
1.________且_______一条线段的直线叫作这条 线段的垂直平分线.
3.如图,直线l 是线段AB的垂直平分线, 则PC____AB,AC=____,PA=_____.
2.线段垂直平分线上的点 ____________________________________
到这条线段两个端点的距离相等
4.____点确定一条直线.
如图,现在知道点C到线段AB 两端的距离相等,即CA=CB,点D到线段AB 两端的距离也相等,即DA=DB,那么根据上面条件你能画出线段AB的垂直平分线吗?
线段的垂直平分线(2)
1.理解掌握线段的垂直平分线的性质定理 的逆定理,并会应用这个逆定理判断一 个点是否在线段的垂直平分线上.
2.能够运用直尺和圆规作出一条线段的垂 直平分线.
1.想一想: 我们知道线段垂直平分线上的点到线段两端 的距离相等,反过来,它的逆命题怎么说?
(1) 当点P在线段AB上时,
2.证明:已知一点P到线段AB 两端的 距离PA与PB相等,那么点P在 线段AB的垂直平分线上吗?
到线段两端距离相等的点在线段的垂直平分线上.
显然此时点P在线段AB的垂直平分线上.
因为PA = PB,所以点P为线段AB的中点,
(2) 当点P在线段AB外时,
因此直线PC是线段AB的垂直平分线, 此时点P也在线段AB的垂直平分线上.
∵PA=PB∴点P在线段AB的垂直平分线上
由此得到线段垂直平分线的性质定理的逆定理:
因为PA =PB,所以△PAB是等腰三角形.
过顶点P 作PC⊥AB,垂足为点C
条件:点到线段两端的距离相等
结论:这个点在线段的垂直平分线上
①由CA=CB可知点C在什么 线上?根据是什么?
点C 在线段AB的垂直平分线上
②由DA=DB可知点D在什么线上?根据是什么?
点D也在线段AB的垂直平分线上
③由上可见直线CD是线段AB的垂直平分线吗?
2.已知:如图,在△ABC中,AB,BC的垂直平 分线相交于点O,连接OA,OB,OC. 求证:点O 在AC的垂直平分线上.
根据“到线段两端距离相等的点在线段的垂直平分线上”可知需要证明__________.
∵点O在线段AB的垂直平分线上
∴ 点O 在AC的垂直平分线上
小结:判断证明一个点在线段的垂直平分线上, 需要找出这个点到线段两端的距离相等
1.课本70页练习2 已知:如图,点C,D是线段AB外的两点,且 AC =BC,AD=BD,AB与CD相交于点O. 求证:AO=BO.
∴点C 在线段AB的垂直平分线上
∴点D也在线段AB的垂直平分线上
∴CD为线段AB的垂直平分线
又AB与CD相交于点O
2.如图,在△ABC中,AC=15cm,AB=10cm,E是BC 的中点,若ΔABD的周长是25cm, 求证:DE是线段BC的垂直平分线
由于E是BC的中点,根据线段垂直平分线的定义需要证明___________
∵ΔABD的周长是25cm
∴AB+BD+AD=25cm
∴BD+AD=15cm
又CD+AD=AB=15cm
∴BD+AD=CD+AD
即ΔBDC是等腰三角形
∴DE是线段BC的垂直平分线
如图,已知线段AB,作线段AB的垂直平分线
分析:根据“到线段两端距离相等的点在线段的垂直平分线上”,要作线段AB的垂直平分线,关键是找出到线段AB两端距离相等的两点.
线段的垂直平分线的作法的应用:
因为线段AB的垂直平分线CD与线段AB的交点就是线段AB的中点,所以可以用这种方法作出线段的中点.
2.过一点作已知直线的垂线
由于两点确定一条直线, 因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线.
用尺规完成下列作图(只保留作图痕迹,不要求写出作法).
初中数学湘教版八年级上册3.3 实数教课ppt课件: 这是一份初中数学湘教版八年级上册3.3 实数教课ppt课件,共22页。
湘教版2.4 线段的垂直平分线教课内容ppt课件: 这是一份湘教版2.4 线段的垂直平分线教课内容ppt课件,共10页。PPT课件主要包含了∴OAOB,同理OBOC,∴OAOC等内容,欢迎下载使用。
2020-2021学年1.1 分式图片ppt课件: 这是一份2020-2021学年1.1 分式图片ppt课件,共13页。PPT课件主要包含了用符号语言表达,知识回顾一,分式的乘法法则,分式的除法法则,分母各自乘方,分组计算下面各题,整数指数幂运算性质,知识回顾二,商的乘方,79×10-7等内容,欢迎下载使用。