苏科版九年级下册5.2 二次函数的图象和性质背景图ppt课件

这是一份苏科版九年级下册5.2 二次函数的图象和性质背景图ppt课件，共15页。PPT课件主要包含了1-2，2-6，直线x-3，直线x1，直线x3，直线x2，二次函数的图象，yax2+bx+c，x10，x20等内容，欢迎下载使用。

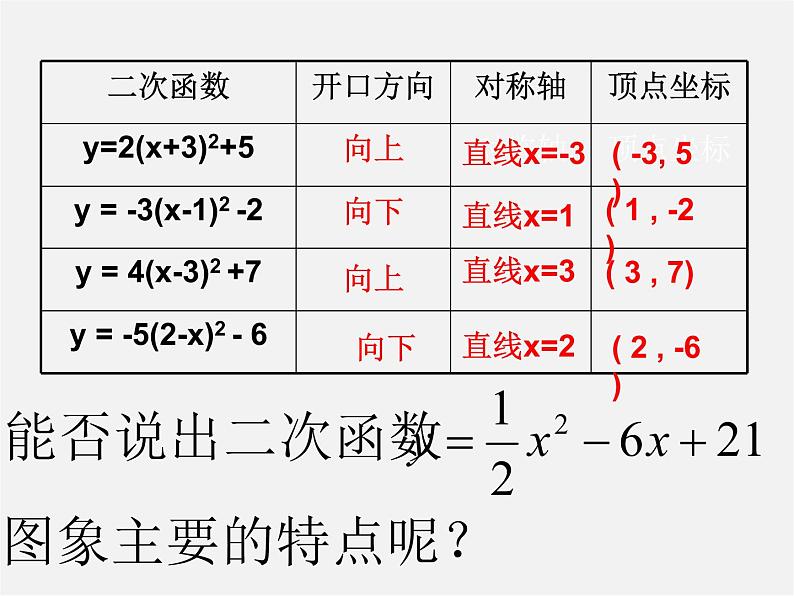
所以,顶点坐标是(-3,2),对称轴是x= -3．
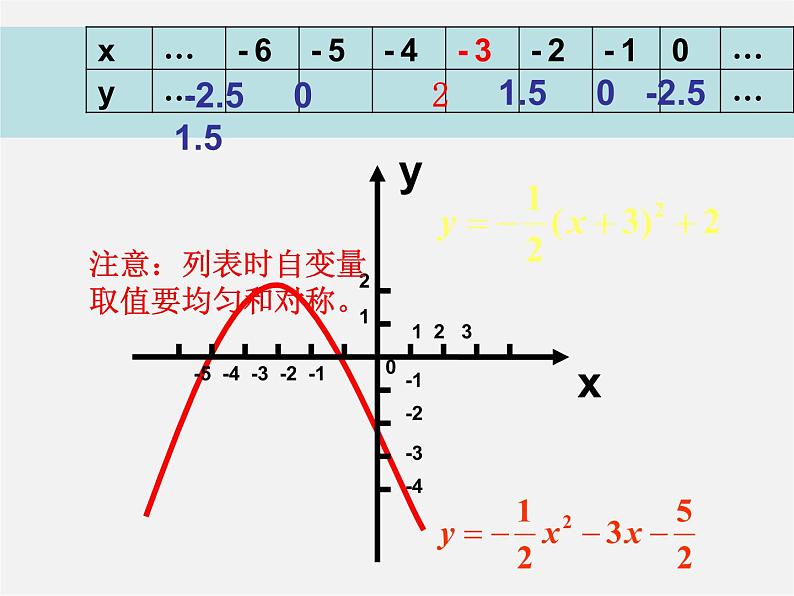
1.5 0 -2.5
-2.5 0 1.5
注意：列表时自变量取值要均匀和对称。
抛物线y=ax2+bx+c(a≠0)可由抛物线y=ax2上下或左右平移得到
一提二配三变形,一般式化为顶点式
左加右减自变量,上加下减常数项
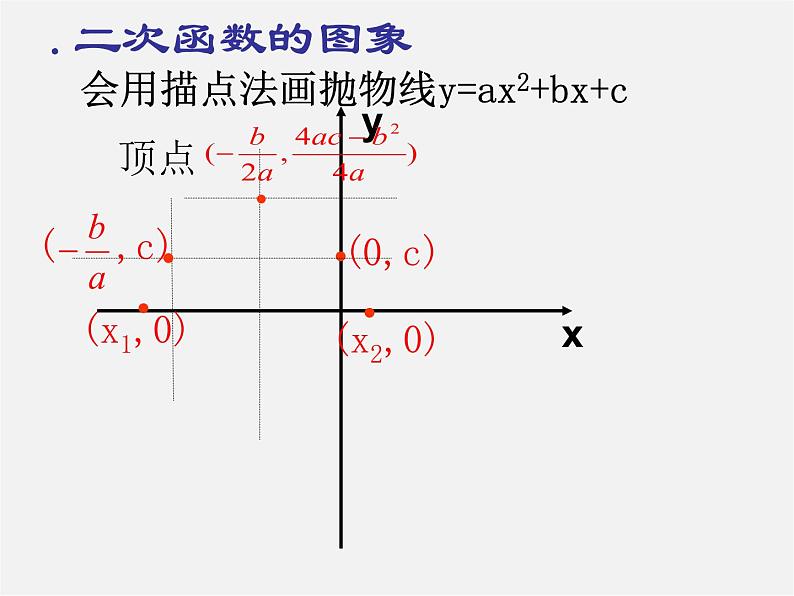
对称轴： x= –
顶点坐标：（– ， ）
会用描点法画抛物线y=ax2+bx+c
解：（1）∵a=－0.5,b=－7,c=7.5;
所以函数y=－0.5x2－7x＋7.5的大致图像如图：
⑵自变量x在什么范围内时，y随x 的增大而增大？何时y 随x的增大而减小？并求出函数的最大值或最小值。
解： ⑵由右图可知，当x≤－7时， y随x 的增大而增大；
当x≥－7 时，y 随x的增大而减小；
当x＝－7时，函数有最大值32。
解： ⑴ ∵y=2x2－8x＋1＝2(x－2)2－7
∴当x=2时,y有最小值,为－7
⑵ ∵a=－3＞0且b=－5,c=1;
故:当x= 时，y有最 值，为
2、已知函数y=x2－3x－4.⑴求函数图像的顶点坐标、与坐标轴交点的坐标和对称轴，并画出函数的大致图像；
解：∵ y=x2－3x－4 ＝(x－1.5)2－6.25,∴图象顶点坐标为(1.5, －6.25);
又当y=0时，得x2－3x－4＝0的解为： x1＝－1，x2＝4。则与x轴的交点为(－1,0)和(4,0)
与y轴的交点为(0, －4)
解:⑵如右图可知: y2＞ y1 ＞ y3
二次函数y=ax2+bx+c(a≠0)的图象和性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
4、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同，则a= .
1、二次函数y=x2+1的图象的顶点坐标是 .
5、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .
6、二次函数y=x2-2x+2 当x= 时，y的最小值为 .
2、将抛物线y=x2+3向右平移2个单位后，所得抛物线的顶点坐标是 。
3.将抛物线y=5x2向左平移2个单位，再向下平移 3个单位，得到的抛物线是_________
y=5(x＋2)2－3