2019-2020八年级（上）期末数学试卷

这是一份2019-2020八年级（上）期末数学试卷，共22页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1. 纳米是长度单位，纳米技术已广泛应用于各个领域，已知1纳米＝0.000000001米，某原子的直径大约是2纳米，用科学记数法表示该原子的直径约为（ ）
A.0.2×10−9米B.2×10−8米C.2×10−9米D.2×10−10米

2. 下列运算正确的是（ ）
A.a2⋅a3＝a6B.(a2)3＝a5C.(2a2)3＝8a6D.a6÷a2＝a3

3. 若分式x+2x−2的值为0，则x的值是（ ）
A.−2B.2C.±2D.任意实数

4. 下列各式中，从左到右的变形是因式分解的是（ ）
A.4x2+8x−1＝4x(x+2)−1B.(x+3)(x−3)＝x2−9
C.x2−x+1＝(x−1)2D.x2−5x−6＝(x+1)(x−6)

5. 下列分式中，是最简分式的是( )
A.9b3aB.a−bb−aC.a2−4a−2D.a2+4a+2

6. 运用乘法公式计算(2x+y−3)(2x−y+3)，下列结果正确的是（ ）
A.4x2−y2−6y+9B.4x2−y2+6y−9
C.4x2+y2−6y+9D.4x2−y2−6y−9

7. 一个三角形的两边长分别为2和5，且第三边长为整数，这样的三角形的周长最大值是（ ）
A.11B.12C.13D.14

8. 一个圆柱形容器的容积为2Vm3，开始用一个小水管向容积内注水，水面高度达到容积的一半后，改用一根口径（直径）为小水管2倍的大水管注水，向容器中注满水的全过程共用时间tmin设小水管的注水速度为xm3/min，则下列方程正确的是（ ）
A.Vx+V2x=tB.Vx+V4x=tC.Vx+V4x=2tD.V2x+V4x=t

9. 将大小不同的两个正方形按图1，图2的方式摆放．若图1中阴影部分的面积是20，图2中阴影部分的面积是14，则大正方形的边长是（ ）

A.6B.7C.8D.9

10. 如图，在Rt△ABC中，∠ACB＝90∘，点D在AB上，连接CD，将△BCD沿直线CD翻折后，点B恰好落在边AC的E点处，若CE:AE＝5:3，S△ABC＝20，则点D到AC的距离是（ ）

A.4013B.2013C.4D.3
二、填空题（共6小题，每小题3分，共18分）

分式xx+1有意义的条件是________．

若am⋅a2=a7，则m的值为________．

如果4x2−mxy+9y2是一个完全平方式，则m＝________．

已知实数a，b满足a−b＝3，ab＝2，则a+b的值为________．

式子3−x2+4x+7的最大值为________．

问题背景：
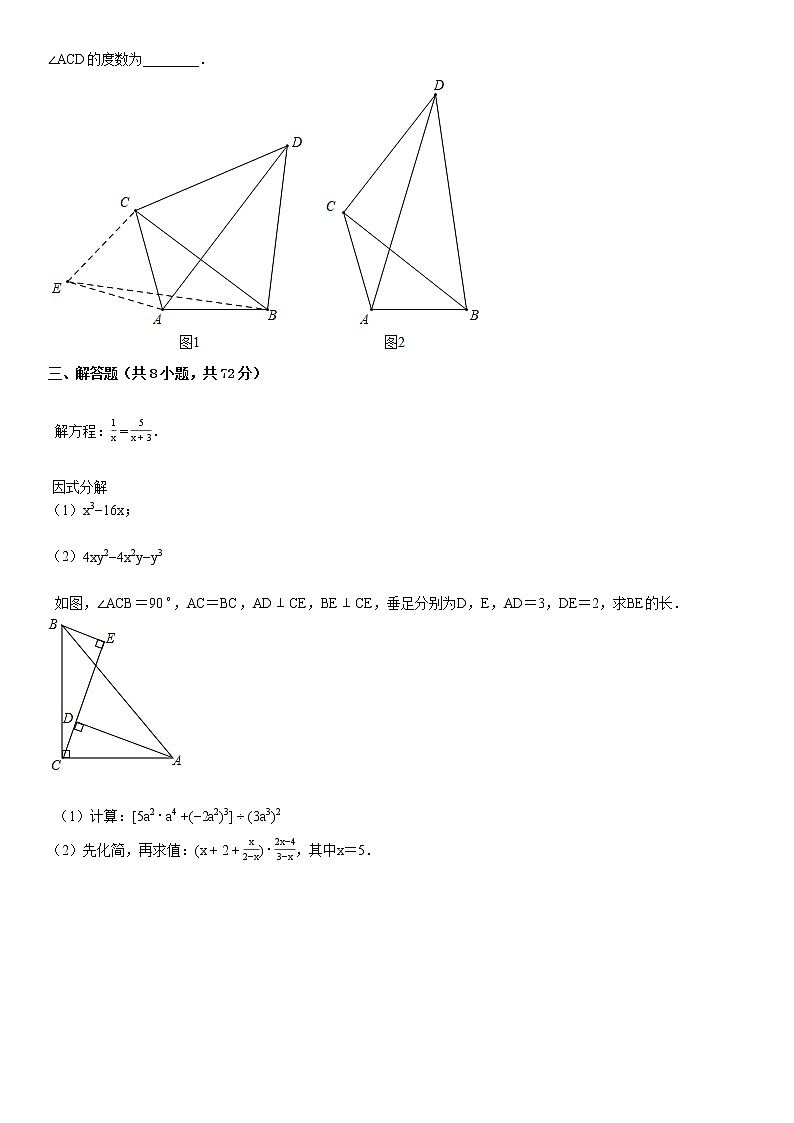
如图1，点C为线段AB外一动点，且AB＝AC＝2，若BC＝CD，∠BCD＝60∘，连接AD，求AD的最大值．
解决方法：
以AC为边作等边△ACE，连接BE，推出BE＝AD，当点E在BA的延长线上时，线段AD取得最大值4．
问题解决：
如图2，点C为线段AB外一动点，且AB＝AC＝2，若BC＝CD，∠BCD＝90∘，连接AD，当AD取得最大值时，∠ACD的度数为________．

三、解答题（共8小题，共72分）

解方程：1x=5x+3．

因式分解
（1）x3−16x；

（2）4xy2−4x2y−y3

如图，∠ACB＝90∘，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD＝3，DE＝2，求BE的长．


（1）计算：[5a2⋅a4+(−2a2)3]÷(3a3)2
（2）先化简，再求值：(x+2+x2−x)⋅2x−43−x，其中x＝5．

如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点，△ABC的顶点在格点，请选择适当的格点，用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．

(1)如图1，作△ABC关于直线l的对称图形△A1B1C1；

(2)如图2，作△ABC的高CD；

(3)如图3，作△ABC的中线CE；

(4)如图4，在直线l上作出一条长度为1个单位长度的线段MN（M在N的上方），使AM+MN+NB的值最小．

两个工程队共同参与一项筑路工程．若先由甲、乙两队合作30天，剩下的工程再由乙队单独做15天可以完成，共需施工费810万元若由甲、乙合作完成此项工程共需36天，共需施工费828万元．
（1）求乙队单独完成这项工程需多少天

（2）甲、乙两队每天的施工费各为多少万元？

（3）若工程预算的总费用不超过840万元，则乙队最少施工多少天？

在等边△ABC中，点E，F分别在边AB，BC上．

（1）如图1，若AE＝BF，以AC为边作等边△ACD，AF交CE于点O，连接OD．
求证：①AF＝CE；
②OD平分∠AOC；

（2）如图2，若AE＝2CF，作∠BCP＝∠AEC，CP交AF的延长线于点P，求证：CE＝CP．

在Rt△ABC中，AC=BC，∠ACB=90∘，点D是BC上一点．
(1)如图1，AD平分∠BAC，求证：AB=AC+CD；

(2)如图2，点E在线段AD上，且∠CED=45∘，∠BED=30∘，求证：BE=2AE；

(3)如图3，CD=BD，过B点作BM⊥AD交AD的延长线于点M，连接CM，过C点作CN⊥CM交AD于N，求证：DN=3DM．
参考答案与试题解析
2019-2020学年湖北省武汉市东西湖区、硚口区八年级（上）期末数学试卷
一、选择题（共10小题，每小题3分，共30分）下列各題中均有四个备选答案，其中有且只有一个正确，请在答题卡上将正确答案的字母代号涂黑
1.
【答案】
C
【考点】
科学记数法--表示较小的数
【解析】
小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】
解：∵ 1纳米＝0.000 000 001米＝10−9米，
∴ 2纳米＝2×10−9米．
故选C.
2.
【答案】
C
【考点】
幂的乘方与积的乘方
同底数幂的除法
同底数幂的乘法
【解析】
根据同底数幂的乘除法和幂的乘方、积的乘方可以计算出各个选项中式子的正确结果，从而可以解答本题．
【解答】
∵ (a2)3＝a6，故选项B错误（1）∵ (2a2)3＝8a6，故选项C正确（2）∵ a6÷a2＝a4，故选项D错误（3）故选：C．
3.
【答案】
A
【考点】
分式值为零的条件
【解析】
直接利用分式的值为零则分子为零进而得出答案．
【解答】
∵ 分式x+2x−2的值为0，
∴ x+2＝0，
解得：x＝−2．
4.
【答案】
D
【考点】
因式分解
因式分解-十字相乘法
因式分解的概念
【解析】
根据分解因式的定义：把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式即可判断．
【解答】
根据分解因式的定义可知：
D选项是把一个多项式化为几个整式的积的形式，
这种变形叫做把这个多项式因式分解，
5.
【答案】
D
【考点】
最简分式
【解析】
根据最简分式的定义：一个分式的分子与分母没有公因式时，叫最简分式即可判断．
【解答】
解：A，原式=3ba，所以A选项不符合题意；
B，原式＝−1，所以B选项不符合题意；
C，原式＝a+2，所以C选项不符合题意；
D，原式是最简分式．
故选D.
6.
【答案】
B
【考点】
平方差公式
完全平方公式
【解析】
原式利用平方差公式变形，再利用完全平方公式展开即可．
【解答】
原式＝4x2−(y−3)2＝4x2−y2+6y−9．
7.
【答案】
C
【考点】
三角形三边关系
【解析】
先根据三角形的三边关系定理求得第三边的取值范围；再根据第三边是整数，从而求得周长最大时，对应的第三边的长．
【解答】
设第三边为a，
根据三角形的三边关系，得：5−2