



_2021年中考一轮复习课件3.3 反比例函数
展开考点一 反比例函数的图象与性质
1.(2020辽宁营口,5,3分)反比例函数y= (x<0)的图象位于 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限
2.(2020山西,7,3分)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y= (k<0)的图象上,且x1
答案 A ∵k<0,∴当x<0时,y随x的增大而增大且y>0,当x>0时,y随x的增大而增大且y<0,又∵x1
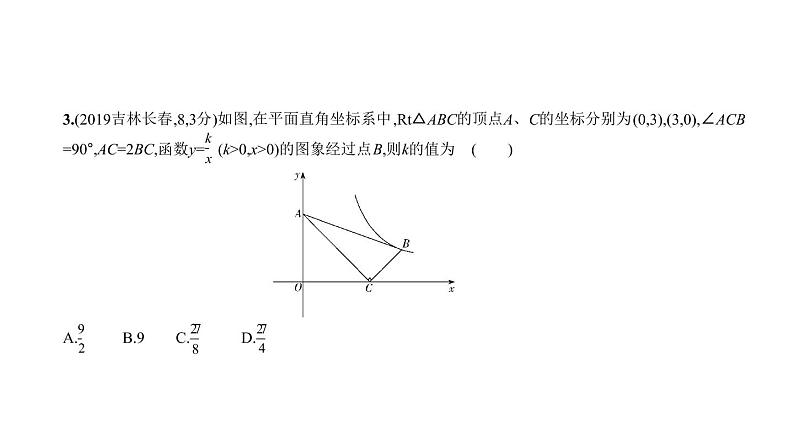
3.(2019吉林长春,8,3分)如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3),(3,0),∠ACB =90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为 ( ) A. B.9 C. D.
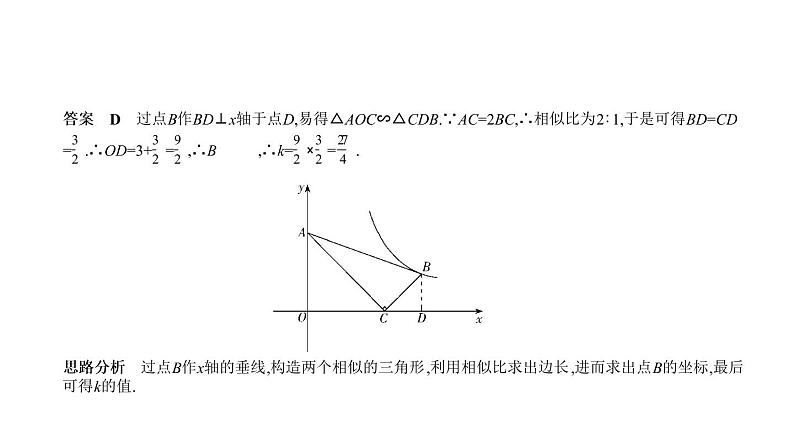
答案 D 过点B作BD⊥x轴于点D,易得△AOC∽△CDB.∵AC=2BC,∴相似比为2∶1,于是可得BD=CD = .∴OD=3+ = ,∴B ,∴k= × = .
思路分析 过点B作x轴的垂线,构造两个相似的三角形,利用相似比求出边长,进而求出点B的坐标,最后 可得k的值.
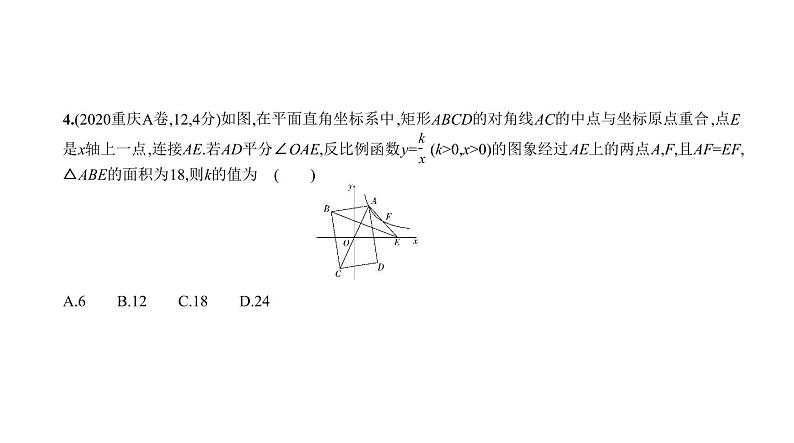
4.(2020重庆A卷,12,4分)如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E 是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 ( ) A.6 B.12 C.18 D.24
答案 B 连接BD,∵AD平分∠OAE,∴∠OAD=∠EAD,∵四边形ABCD是矩形,∴OA=OD,∴∠ODA=∠ OAD,∴∠ODA=∠EAD,∴BD∥AE,∴△AOE与△ABE的面积相等,为18,又∵AF=EF,∴△OEF的面积为 9,设F ,∵F为AE的中点且A点在反比例函数y= (k>0,x>0)的图象上,∴A ,过A作AM⊥x轴于M,过F作FN⊥x轴于N,则OM= ,MN= ,又∵AF=EF,∴MN=NE,∴△OFN的面积为△OEF面积的 ,为6,∴k=2S△OFN=12.
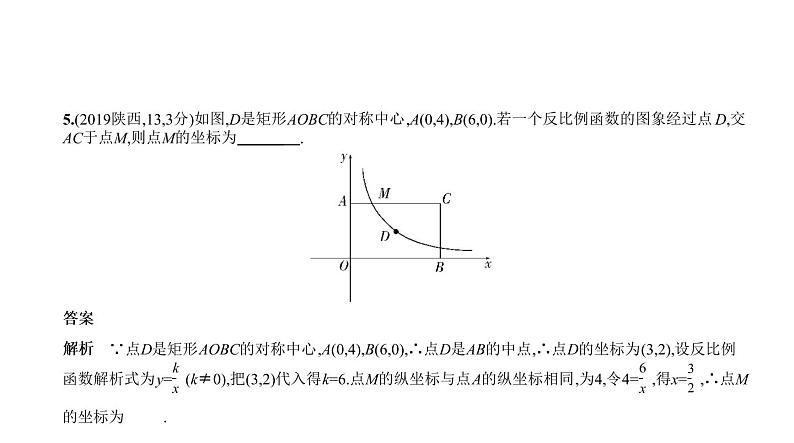
5.(2019陕西,13,3分)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0).若一个反比例函数的图象经过点D,交 AC于点M,则点M的坐标为 .
6.(2019内蒙古包头,19,3分)如图,在平面直角坐标系中,已知A(-1,0),B(0,2),将△ABO沿直线AB翻折后得 到△ABC,若反比例函数y= (x<0)的图象经过点C,则k= .
7.(2020吉林,21,7分)如图,在平面直角坐标系中,O为坐标原点,点A,B在函数y= (x>0)的图象上(点B的横坐标大于点A的横坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接OA,AB.(1)求k的值;(2)若D为OC的中点,求四边形OABC的面积.
解析 (1)把(2,4)代入y= ,得4= .解得k=8. (3分)(2)∵点A的坐标是(2,4),∴OD=2,AD=4.∵D为OC的中点,∴OC=2OD=4. (4分)当x=4时,y= =2,∴点B的坐标是(4,2),∴BC=2. (5分)∴S四边形OABC=S△AOD+S四边形ABCD= ×2×4+ ×(2+4)×2=10.
∴四边形OABC的面积是10. (7分)
思路分析 (1)将点A的坐标代入y= ,可得k值;(2)将点C的横坐标代入反比例函数的解析式可得点B的纵坐标,利用三角形和梯形的面积公式可得结果.
8.(2020江西,18,8分)如图,Rt△ABC中,∠ACB=90°,顶点A,B都在反比例函数y= (x>0)的图象上,直线AC⊥x轴,垂足为D,连接OA,OC,并延长OC交AB于点E,当AB=2OA时,点E恰为AB的中点,若∠AOD=45°,OA=2 .(1)求反比例函数的解析式;(2)求∠EOD的度数.
解析 (1)∵AD⊥x轴,∠AOD=45°,OA=2 ,∴AD=OD=2.∴A(2,2).∵点A在反比例函数图象上,∴k=2×2=4.∴y= .(2)∵△ABC为直角三角形,点E为AB的中点,∴AE=CE=EB,∴∠AEC=2∠ECB.∵AB=2OA,∴AO=AE.∴∠AOE=∠AEO=2∠ECB.∵∠ACB=90°,AD⊥x轴,∴BC∥x轴.
∴∠ECB=∠EOD.∴∠AOE=2∠EOD.∵∠AOD=45°,∴∠EOD= ∠AOD= ×45°=15°.
9.(2019甘肃兰州,23,7分)如图,在平面直角坐标系xOy中,反比例函数y= (k≠0)的图象过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,AO.(1)求反比例函数y= (k≠0)的表达式;(2)若四边形ACBO的面积是3 ,求点A的坐标.
解析 (1)∵OC=2,且△BOC为等边三角形,∴B(-1,- ),∴k=(-1)×(- )= ,∴反比例函数表达式为y= .(2)S四边形ACBO=S△BOC+S△AOC,过点A作AN⊥x轴于点N.∵S△BOC= OC2= ,∴ +S△AOC=3 ,∴S△AOC=2 ,即 OC·AN=2 ,又∵OC=2,∴AN=2 ,设A(t,2 ),∴2 t= ,∴t= ,即点A的坐标为 .
考点二 反比例函数与一次函数的综合应用
1.(2020宁夏,7,3分)如图,函数y1=x+1与函数y2= 的图象相交于点M(1,m),N(-2,n).若y1>y2,则x的取值范围是 ( ) A.x<-2或0
方法总结 解决这类题的方法就是数形结合,抓住两个图象的交点的横坐标.
2.(2020内蒙古包头,11,3分)如图,在平面直角坐标系中,直线y=- x+3与x轴、y轴分别交于点A和点B,C是线段AB上一点,过点C作CD⊥x轴,垂足为D,CE⊥y轴,垂足为E,S△BEC∶S△CDA=4∶1,若双曲线y= (x>0)经过点C,则k的值为 ( ) A. B. C. D.
答案 A 由题意知四边形EODC是矩形.已知y=- x+3,令x=0,得y=3,∴B(0,3),∴OB=3,令y=0,则- x+3=0,解得x=2,∴A(2,0),∵CD⊥x轴,∴CD∥y轴,∴∠ACD=∠CBE,又∠CDA=∠BEC,∴△BEC∽△CDA.∵S△BEC∶S△CDA=4∶1,∴BE∶CD=2∶1,又∵OB=3,∴CD=1,将y=1代入y=- x+3,得- x+3=1,解得x= ,∴C ,将 代入y= (x>0),得1= ,解得k= .
3.(2017甘肃兰州,11,4分)如图,反比例函数y= (x<0)与一次函数y=x+4的图象交于A,B两点,A,B两点的横坐标分别为-3,-1,则关于x的不等式
4.(2019江西,5,3分)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是 ( )A.反比例函数y2的解析式是y2=- B.两个函数图象的另一交点坐标为(2,-4)C.当x<-2或0
6.(2019新疆,15,5分)如图,在平面直角坐标系xOy中,已知正比例函数y=-2x与反比例函数y= 的图象交于A(a,-4),B两点.过原点O的另一条直线l与双曲线y= 交于P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是 .
答案 (-4,2)或(-1,8)
∵点P,B在双曲线上,∴S△POM=S△BON=4,∵S△BON+S梯形PMNB=S△POB+S△POM,∴S梯形PMNB=S△POB=6,∴ ·(-2-m)=6,解得m=-4或m=1(舍去),
∴P(-4,2).②当-2
7.(2019贵州贵阳,22,10分)如图,已知一次函数y=-2x+8的图象与坐标轴交于A,B两点,并与反比例函数y= 的图象相切于点C.(1)切点C的坐标是 ;(2)若点M为线段BC的中点,将一次函数y=-2x+8的图象向左平移m(m>0)个单位后,点C和点M平移后的对 应点同时落在另一个反比例函数y= 的图象上时,求k的值.
解析 (1)令-2x+8= ,得x2-4x+4=0(x≠0),解得x1=x2=2,则y=4,∴切点C的坐标为(2,4).故填(2,4).(2)由(1)可知C(2,4),∵直线y=-2x+8与x轴交于点B,∴B(4,0),∴线段BC的中点M(3,2).∵直线AB向左平移m(m>0)个单位,∴点C平移后的对应点的坐标为(2-m,4),点M平移后的对应点的坐标为(3-m,2),∵平移后的对应点同时落在反比例函数y= 的图象上,∴ 解得 ∴k的值是4.
8.(2020四川南充,21,10分)如图,反比例函数y= (k≠0,x>0)的图象与y=2x的图象相交于点C,过直线上点A(a,8)作AB⊥y轴交于点B,交反比例函数图象于点D,且AB=4BD.(1)求反比例函数的解析式;(2)求四边形OCDB的面积.
解析 (1)由点A(a,8)在y=2x的图象上,得a=4,∴A(4,8). (1分)∵AB⊥y轴,与反比例函数图象交于点D,且AB=4BD,∴BD=1,∴D(1,8). (3分)∴k=8,反比例函数的解析式为y= . (5分)(2)∵C是直线y=2x与反比例函数y= (x>0)图象的交点,∴2x= ,又∵x>0,∴x=2,则C(2,4). (7分)∵S△ABO= ×4×8=16, (8分)S△ADC= ×3×4=6, (9分)∴S四边形OCDB=S△ABO-S△ADC=10. (10分)
9.(2020四川成都,19,10分)在平面直角坐标系xOy中,反比例函数y= (x>0)的图象经过点A(3,4),过点A的直线y=kx+b与x轴、y轴分别交于B,C两点.(1)求反比例函数的表达式;(2)若△AOB的面积为△BOC的面积的2倍,求此直线的函数表达式.
解析 (1)∵反比例函数y= 的图象过A(3,4),∴m=3×4=12,∴反比例函数的表达式为y= .(2)连接OA,①当k<0时,直线y=kx+b为图中直线l1,由图象可知, < ,不符合题意,舍去.②当k>0时,若b>0,直线y=kx+b为图中直线l2,过A作AD⊥x轴,垂足为D.∵ =2 , = , = ,∴OC2= AD,∴OB2=OD.又∵A(3,4),∴AD=4,OD=3,∴B2O=OD=3,OC2=2,∴B2(-3,0),C2(0,2),∴y= x+2.若b<0,直线y=kx+b为图中直线l3,
同理可得,B3O= B3D,OC3= AD,∴B3O=1,OC3=2,∴B3(1,0),C3(0,-2),∴y=2x-2.综上所述,直线的函数表达式为y= x+2或y=2x-2.
10.(2019辽宁大连,22,9分)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y= (x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.(1)求该反比例函数的解析式;(2)若S△ACD= ,设点C的坐标为(a,0),求线段BD的长.
解析 (1)将(3,2)代入y= 中,得2= ,解得k=6,所以该反比例函数的解析式为y= (x>0).(2)过A作AE⊥BC于点E,延长EA交y轴于点F, ∵点A的坐标为(3,2),∴AF=3,
∵BC⊥x轴,点C的坐标为(a,0),∴点D的坐标为 ,AE=a-3.∵S△ACD= CD·AE= · ·(a-3)= ,∴a=6,经检验,a=6是上述分式方程的解.∴点D的坐标为(6,1).设OA所在直线的解析式为y=mx(m≠0),将(3,2)代入,得2=3m,解得m= ,∴OA所在直线的解析式为y= x,当x=6时,y= ×6=4.∴点B的坐标为(6,4).
考点三 反比例函数的实际应用(2020云南昆明,19,8分)为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消 毒,她完成3间办公室和2间教室的药物喷洒要19 min,完成2间办公室和1间教室的药物喷洒要11 min.(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示.校医进 行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点 为A(m,n).当教室空气中的药物浓度不高于1 mg/m3时,对人体健康无危害.校医依次对一班至十一班教室 (共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算 说明.
解析 (1)设校医完成一间办公室的药物喷洒要a min,完成一间教室的药物喷洒要b min. (1分)根据题意得 (3分)解得 (4分)答:校医完成一间办公室的药物喷洒要3 min,完成一间教室的药物喷洒要5 min. (5分)(2)由(1)得,m=5,则n=2×5=10,∴A(5,10).设药物喷洒完成后y与x的函数解析式为y= (k≠0),则10= ,解得k=50,∴y= (x≥5), (7分)当y≤1时,即 ≤1,解得x≥50,∵11×5=55 min>50 min,∴当校医把最后一间教室药物喷洒完成后,一班学生能进入教室. (8分)
1.(2020湖北武汉,7,3分)若点A(a-1,y1),B(a+1,y2)在反比例函数y= (k<0)的图象上,且y1>y2,则a的取值范围是 ( )A.a<-1 B.-1
解题关键 判断点A在第二象限,点B在第四象限是解答本题的关键.
2.(2019安徽,5,4分)已知点A(1,-3)关于x轴的对称点A'在反比例函数y= 的图象上,则实数k的值为 ( )A.3 B. C.-3 D.-
3.(2019河北,12,2分)如图,函数y= 的图象所在坐标系的原点是 ( ) A.点M B.点N C.点P D.点Q
4.(2020辽宁营口,10,3分)如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为 ( ) A.3 B. C.2 D.1
答案 C 如图,过点C作CE⊥OA于点E,则CE∥AB,所以△OCE∽△OBA.又因为C是OB的中点,所以S△O- BA=4S△OCE.由反比例函数系数k的几何意义可知S△OCE=S△OAD=0.5k,所以S△OBA=2k,所以S△OBD=1.5k.因为S△OCD= ,C是OB的中点,所以S△OBD=3,所以k=2.
解后反思 本题需要借助反比例函数系数k的几何意义以及相似三角形的相关知识解决.
5.(2019湖北武汉,8,3分)已知反比例函数y= 的图象分别位于第二、第四象限,A(x1,y1),B(x2,y2)两点在该图象上.下列命题:①过点A作AC⊥x轴,C为垂足,连接OA,若△ACO的面积是3,则k=-6;②若x1<0
6.(2020云南,4,3分)已知一个反比例函数的图象经过点(3,1),若该反比例函数的图象也经过点(-1,m),则m = .
解析 ∵点(3,1)和点(-1,m)在同一个反比例函数的图象上,∴3×1=-m,则m=-3.
7.(2020陕西,13,3分)在平面直角坐标系中,点A(-2,1),B(3,2),C(-6,m)分别在三个不同的象限.若反比例函数 y= (k≠0)的图象经过其中两点,则m的值为 .
8.(2020黑龙江齐齐哈尔,16,3分)如图,在平面直角坐标系中,矩形ABCD的边AB在y轴上,点C坐标为(2,-2), 并且AO∶BO=1∶2,点D在函数y= (x>0)的图象上,则k的值为 .
9.(2019云南,4,3分)若点(3,5)在反比例函数y= (k≠0)的图象上,则k= .
10.(2019甘肃兰州,15,4分)如图,矩形OABC的顶点B在反比例函数y= (x>0)的图象上,S矩形OABC=6,则k= .
解析 ∵矩形OABC的面积等于6,∴BC·BA=6,即xy=6,∴k=6.
11.(2019北京,13,2分)在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y= 上,点A关于x轴的对称点B在双曲线y= 上,则k1+k2的值为 .
解题关键 解决本题的关键是通过表示对称点的坐标求出k1和k2与ab的关系,进而化简得到答案.
12.(2018内蒙古包头,19,3分)以矩形ABCD两条对角线的交点O为坐标原点,以平行于两边的直线为坐标 轴,建立如图所示的平面直角坐标系,BE⊥AC,垂足为E.若双曲线y= (x>0)经过点D,则OB·BE的值为 .
13.(2019山西,14,3分)如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上, 点A的坐标为(-4,0),点D的坐标为(-1,4),反比例函数y= (x>0)的图象恰好经过点C,则k的值为 .
解析 过点D作DE⊥AB于点E,则AD=5,∵四边形ABCD为菱形,∴CD=5,∴C(4,4),将C点坐标代入y= 得4= ,∴k=16.
14.(2019山东潍坊,15,3分)如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y= (x>0)与y= (x<0)的图象上,则tan∠BAO的值为 .
思路分析 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,于是得到∠BDO=∠ACO=90°,根据反比例 函数的比例系数k的几何意义得到S△BDO= ,S△AOC= ,证明△BDO∽△OCA,然后根据相似三角形的性质得到 = = =5,求得 = ,根据正切函数的定义即可得到答案.
15.(2019福建,16,4分)如图,菱形ABCD的顶点A在函数y= (x>0)的图象上,函数y= (k>3,x>0)的图象关于直线AC对称,且过B,D两点.若AB=2,∠BAD=30°,则k= .
解析 连接AC,过B作BF⊥x轴于F,过A作AM⊥BF于M.如图. 由双曲线的对称性可知,点A,C是第一象限角平分线上的点,即xA=yA,∴ =3,即xA= ,∴A( , ).根据题意可得∠CAM=45°,∵∠BAC= ∠BAD= ×30°=15°,∴∠BAM=30°,∴BM= AB= ×2=1.∴AM= = = .∴B(2 ,1+ ).
∴k=2 ×(1+ )=6+2 .
疑难突破 本题的突破口是得到∠CAM=45°,能将点的坐标转化为线段长,构建含30°角的Rt△ABM.
16.(2019吉林,17,5分)已知y是x的反比例函数,并且当x=2时,y=6.(1)求y关于x的函数解析式;(2)当x=4时,求y的值.
1.(2018四川遂宁,7,4分)已知一次函数y1=kx+b(k≠0)与反比例函数y2= (m≠0)的图象如图所示,则当y1>y2时,自变量x满足的条件是 ( ) A.1
答案 A ∵y1>y2,∴根据图象可得当1
答案 C 延长BD交y轴于E,延长CA交y轴于F,设C ,D ,则FC=n,DE=m,∵点A,B在直线y=x上,∴OF=AF= ,OE=BE= , 故BD=BE-DE= -m,AC=FC-AF=n- ,∵ BD=AC,∴ =n- ,
∴3 = ,整理得3 - =4,又3OD2=3(OE2+DE2)=3 ,OC2=FC2+OF2=n2+ ,∴3OD2-OC2=3 - =4.故选C.
3.(2018安徽,13,5分)如图,正比例函数y=kx与反比例函数y= 的图象有一个交点A(2,m),AB⊥x轴于点B.平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表达式是 .
4.(2020四川成都,24,4分)在平面直角坐标系xOy中,已知直线y=mx(m>0)与双曲线y= 交于A,C两点(点A在第一象限),直线y=nx(n<0)与双曲线y=- 交于B,D两点.当这两条直线互相垂直,且四边形ABCD的周长为10 时,点A的坐标为 .
答案 ( ,2 )或(2 , )
联立 得- x2+1=0,∴B ,∴OB2= +( )2= +m.∵OA=OC,OB=OD,AC⊥BD,∴四边形ABCD为菱形.∵四边形ABCD的周长为10 ,∴AB= ,在Rt△OAB中,OA2+OB2=AB2,∴ +4m+ +m= ,化简得m2- m+1=0,解得m=2或m= ,∴点A的坐标为( ,2 )或(2 , ).
5.(2020内蒙古呼和浩特,20,6分)已知自变量x与因变量y1的对应关系如下表呈现的规律.
解析 (1)根据题表中的数据发现:y1和x的和为10,∴y1=10-x,且当x=0时,y1=10,令y1=0,得x=10,∴M(10,0),N(0,10).(2)设A(m,10-m),B(n,10-n),分别过A和B作x轴的垂线,垂足为C和D,如图,S△AOB=S△AOM-S△OBM= ×10×(10-m)- ×10×(10-n)=30,化简得n-m=6,令y1=y2,得x2-10x+k=0,∴m+n=10,mn=k,∴n-m= =6,则 =6,解得k=16,∴反比例函数解析式为y2= ,解x2-10x+16=0,得x=2或x=8,∴A(2,8),B(8,2),
∵(a,y2)在反比例函数y2= 的图象上,(a,y1)在一次函数y1=10-x的图象上,∴当0
解析 (1)∵一次函数y=x+1的图象与反比例函数y= 的图象的一个交点的横坐标是2,且当x=2时,y=3,∴其中一个交点是(2,3).∴k=2×3=6.∴反比例函数的表达式是y= .(2)将一次函数y=x+1的图象向下平移2个单位,平移后的图象对应的表达式是y=x-1.由xy=6及y=x-1,可得一元二次方程x2-x-6=0,解得x1=-2,x2=3.∴平移后的图象与反比例函数的图象的交点坐标为(-2,-3),(3,2).(3)y=-2x+5(答案不唯一).
7.(2019广东,23,9分)如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A、B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n). (1)根据图象,直接写出满足k1x+b> 的x的取值范围;(2)求这两个函数的表达式;(3)点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
解析 (1)x<-1或0
∴S△BOP= S△AOB= × =5.∵点P在线段AB上,∴可设P的坐标为(m,-m+3)(-1
8.(2019内蒙古呼和浩特,23,7分)如图,在平面直角坐标系中,矩形OCAB(OC>OB)的对角线长为5,周长为1 4.若反比例函数y= 的图象经过矩形顶点A.(1)求反比例函数解析式;若点(-a,y1)和(a+1,y2)在反比例函数的图象上,试比较y1与y2的大小;(2)若一次函数y=kx+b的图象过点A并与x轴交于点(-1,0),求出一次函数解析式,并直接写出kx+b- <0成立时,对应x的取值范围.
解析 (1)设A点的坐标为(x,y),则x2+y2=25,∴(x+y)2-2xy=25,又x+y=7,∴xy=12,∴m=12,反比例函数解析式为y= .①当a<-1时,a+1<0<-a,此时y1>0>y2;②当-1
9.(2019广东广州,22,12分)如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB ⊥x轴于点E,正比例函数y=mx的图象与反比例函数y= 的图象相交于A,P两点.(1)求m,n的值与点A的坐标;(2)求证:△CPD∽△AEO;(3)求sin∠CDB的值.
解析 (1)将点P(-1,2)代入y=mx,得2=-m,解得m=-2,所以正比例函数解析式为y=-2x.将点P(-1,2)代入y= ,得2=-(n-3),解得n=1,所以反比例函数解析式为y=- .由于正比例函数与反比例函数图象的交点关于原点对称,所以点A的坐标为(1,-2).(2)证明:∵四边形ABCD是菱形,∴AC⊥BD,AB∥CD,∴∠CPD=90°,∠DCP=∠OAE,∵AB⊥x轴,∴∠AEO =90°,∴∠AEO=∠CPD,∴△CPD∽△AEO.(3)∵点A的坐标为(1,-2),∴AE=2,OE=1,∴AO= = ,∴sin∠AOE= = = ,∵△CPD∽△AEO,∴∠CDB=∠AOE,∴sin∠CDB=sin∠AOE= .
思路分析 (1)根据点P的坐标,利用待定系数法可求出m,n的值,通过正比例函数和反比例函数图象的交 点关于原点对称可以得到点A的坐标.(2)由菱形的性质可得出AC⊥BD,AB∥CD,利用平行线的性质可得出∠DCP=∠OAE,结合AB⊥x轴可得 出∠AEO=∠CPD=90°,即可证出△CPD∽△AEO.(3)由点A的坐标可得出AE,OE,AO的长,由相似三角形的性质可得出∠CDB=∠AOE,再利用正弦的定义 即可求出sin∠CDB的值.
10.(2019江苏苏州,25,8分)如图,A为反比例函数y= (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA,AB,且OA=AB=2 .(1)求k的值;(2)过点B作BC⊥OB,交反比例函数y= (其中x>0)的图象于点C,连接OC交AB于点D,求 的值.
解析 (1)过点A作AE⊥OB于E.∵OA=AB=2 ,OB=4,∴OE=BE= OB=2,在Rt△OAE中,AE= = =6,∴点A的坐标为(2,6).∵点A是反比例函数y= 图象上的点,∴6= ,解得k=12.
(2)记AE与OC的交点为F.∵OB=4且BC⊥OB,∴点C的横坐标为4.又∵点C为反比例函数y= 图象上的点,∴点C的坐标为(4,3),∴BC=3.设直线OC的表达式为y=mx,m≠0,将C(4,3)代入可得m= ,∴直线OC的表达式为y= x.∵AE⊥OB,OE=2,∴点F的横坐标为2,将x=2代入y= x可得y= ,即EF= .∴AF=AE-EF=6- = .∵AE,BC都与x轴垂直,∴AE∥BC,
∴∠AFD=∠BCD,∠FAD=∠CBD,∴△ADF∽△BDC,∴ = = .
11.(2018甘肃白银,25,10分)如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A(-1,a),B两点,与x轴交于点C.(1)求反比例函数的表达式;(2)若点P在x轴上,且S△ACP= S△BOC,求点P的坐标.
解析 (1)∵一次函数y=x+4的图象经过点A(-1,a),∴-1+4=a,∴a=3,∴A点坐标是(-1,3).∵反比例函数y= 的图象经过点A(-1,3),∴k=-1×3=-3.∴反比例函数的表达式是y=- .(2)联立一次函数与反比例函数的解析式得 解得 ∵点A的坐标是(-1,3),∴点B的坐标是(-3,1).∵一次函数y=x+4的图象交x轴于点C,∴C点坐标是(-4,0),∴CO=4.∴S△BOC= CO×|yB|= ×4×1=2.
∵点P在x轴上,∴设点P的坐标是(x,0).∴CP=|x-(-4)|=|x+4|,∴△ACP中CP边上的高就是A点的纵坐标的绝对值,即为3.∴S△ACP= CP×|yA|= |x+4|×3.∵S△ACP= S△BOC,∴ |x+4|×3= ×2,∴|x+4|=2,即x+4=2或x+4=-2,∴x=-2或x=-6,∴点P的坐标是(-2,0)或(-6,0).
思路分析 (1)将点A的坐标代入一次函数解析式中求出A点坐标,然后将A点坐标代入反比例函数解析 式中可求k;(2)设出点P的坐标,然后求出△BOC的面积,建立方程可求出P点坐标.
12.(2018山西,17,8分)如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2= (k2≠0)的图象相交于点C(-4,-2),D(2,4).(1)求一次函数和反比例函数的表达式;(2)当x为何值时,y1>0?(3)当x为何值时,y1
(3)x<-4或0
解析 (1)∵点A(-3,a)在直线y=2x+4上,∴a=2×(-3)+4=-2.∵点A(-3,-2)在y= 的图象上,∴k=6.(2)∵点M是直线y=m与直线AB的交点,∴M .∵点N是直线y=m与反比例函数y= 的图象的交点,∴N .∴MN=xN-xM= - =4或MN=xM-xN= - =4.解得m=2或m=-6或m=6±4 ,∵m>0,∴m=2或m=6+4 .(3)x<-1或5
14.(2017四川成都,19,10分)如图,在平面直角坐标系xOy中,已知正比例函数y= x的图象与反比例函数y= 的图象交于A(a,-2),B两点.(1)求反比例函数的表达式和点B的坐标;(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的 面积为3,求点P的坐标.
解析 (1)∵A(a,-2)在正比例函数y= x的图象上,∴ a=-2,解得a=-4,∴A(-4,-2).∵A(-4,-2)在反比例函数y= 的图象上,∴k=-4×(-2)=8,∴反比例函数的表达式为y= ,联立 ⇒x2=16⇒x=±4,∴B(4,2).(2)设P ,m>0,则C ,
可得PC= ,又△POC中PC边上的高为m,∴S△POC= m· =3,∴m2=28或4,∴m=2 或2,
∴P 或P(2,4).
考点三 反比例函数的实际应用
1.(2020湖南长沙,5,3分)2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四 水,杜娟花开”为设计理念,塑造出“杜娟花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某 运输公司承担了运送总量为106 m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完 成运送任务所需时间t(单位:天)之间的函数关系式是 ( )A.v= B.v=106tC.v= t2 D.v=106t2
2.(2019浙江温州,6,4分)验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表. 根据表中数据,可得y关于x的函数表达式为 ( )
A.y= B.y= C.y= D.y=
3.(2019浙江杭州,20,10分)方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行 驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)求v关于t的函数表达式;(2)方方上午8点驾驶小汽车从A地出发.①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围;②方方能否在当天11点30分前到达B地?说明理由.
解析 (1)根据题意,得vt=480,所以v= .因为480>0,所以当v≤120时,t≥4,所以v= (t≥4).(2)①根据题意,得4.8≤t≤6.因为480>0,所以 ≤v≤ ,所以80≤v≤100.②方方不能在11点30分前到达B地,理由如下:若方方在11点30分前到达B地,则t<3.5,所以v> >120,所以方方不能在11点30分前到达B地.
A组 2018—2020年模拟·基础题组时间:45分钟 分值:55分一、选择题(每小题3分,共9分)
1.(2020天津河北3月模拟,9)对于反比例函数y= ,当x>2时,y的取值范围是 ( )A.y> 或y<0 B.y> C.0
3.(2020上海长宁二模,3)关于反比例函数y= ,下列说法不正确的是 ( )A.点(-2,-1)在它的图象上B.它的图象在第一、三象限C.它的图象关于原点中心对称D.y的值随着x的值的增大而减小
二、填空题(每小题3分,共12分)4.(2020上海宝山二模,14)如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y= 的图象经过点B,则k的值是 .
5.(2020四川成都龙泉驿三诊,13)如果反比例函数y= 在每个象限内y随x的增大而减小,那么m的取值范围是 .
解析 由已知得m+1>0,解得m>-1.
6.(2019新疆乌鲁木齐高新区一模,12)已知直线y=ax(a≠0)与反比例函数y= (k≠0)的图象的一个交点坐标为(2,4),则它们另一个交点的坐标是 .
解析 ∵反比例函数的图象与正比例函数图象的两个交点关于原点对称,∴另一个交点的坐标为(-2,-4).
7.(2019上海嘉定二模,12)已知反比例函数y= 的图象经过点(2,-1),那么k的值是 .
三、解答题(共34分)8.(2020四川成都青白江一诊,19)如图,已知△OAB的顶点B在x轴的负半轴上,AB⊥OB,点A的坐标为(-4, 2),双曲线y= (k<0)的一支经过OA边的中点C,且与AB相交于点D.(1)求此双曲线对应的函数表达式;(2)连接OD,求△AOD的面积.
解析 (1)∵点A的坐标为(-4,2),C是OA的中点,∴C(-2,1).∵双曲线y= (k<0)的一支经过点C,∴k=-2×1=-2,∴双曲线对应的函数表达式为y=- .(2)把x=-4代入y=- ,得y= ,∴D ,∴S△AOD= AD·OB= × ×4=3.
9.(2020甘肃兰州一诊,23)如图,一次函数y=- x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y= (x<0)的图象交于点C(-2,2).(1)求一次函数与反比例函数的解析式;(2)过点B作x轴的平行线交反比例函数的图象于点D,连接CD.求△BCD的面积.
解析 (1)把(-2,2)代入y=- x+b,得1+b=2,解得b=1,∴一次函数解析式为y=- x+1.把(-2,2)代入y= ,得k=-2×2=-4,∴反比例函数解析式为y=- (x<0).(2)在y=- x+1中,令x=0,得y=1,∴B(0,1).∵BD∥x轴,∴D点的纵坐标为1.令- =1,得x=-4,则D(-4,1).∴BD=0-(-4)=4,
∴△BCD的面积为 ×4×(2-1)=2.
10.(2019江西南昌一模,19)如图,在平面直角坐标系中,反比例函数y= 的图象经过点P(4,3)和点B(m,n)(其中0
11.(2019四川成都双流一模,19)如图,在平面直角坐标系中,一次函数y=- x+3的图象与反比例函数y= (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.(1)求反比例函数的表达式;(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积 与四边形OACB的面积相等,求点P的坐标.
解析 (1)∵点A(a,2),B(4,b)在一次函数y=- x+3的图象上,∴- a+3=2,b=- ×4+3,∴a=2,b=1,∴点A的坐标为(2,2),点B的坐标为(4,1).∵点A(2,2)在反比例函数y= (x>0,k是常数)的图象上,∴k=2×2=4,∴反比例函数的表达式为y= (x>0).(2)延长CA交y轴于点E,延长CB交x轴于点F.
∵AC∥x轴,BC∥y轴,∴CE⊥y轴,CF⊥x轴,又A(2,2),B(4,1),∴点C的坐标为(4,2).易知四边形OECF为矩形,且CE=4,CF=2,∴S四边形OACB=S矩形OECF-S△OAE-S△OBF=2×4- ×2×2- ×4×1=4.设点P的坐标为(0,m),则S△OAP= ×2·|m|=4,∴m=±4,∴点P的坐标为(0,4)或(0,-4).
B组 2018—2020年模拟·提升题组时间:45分钟 分值:55分一、选择题(每小题3分,共12分)1.(2020辽宁鞍山铁东一模,7)如图,点A(2,m)在反比例函数y= 的图象上,点B在反比例函数y= 的图象上,OB⊥OA,AB∥y轴,则k的值为 ( ) A.-16 B.-8 C.-6 D.-4
答案 B 过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,如图.∵点A(2,m)在反比例函数y= 的图象上,∴m= =1,∴AC=2,OC=1.又∵AB∥y轴,点B在反比例函数y= 的图象上,∴B ,∴BD=2,OD=- .∵OB⊥OA,∠ACO=∠ODB=90°,∴∠AOC+∠BOD=∠AOC+∠OAC=90°,∴∠OAC=∠BOD,∴△AOC∽△OBD,∴ = ,即 = ,∴OD=4,∴k=2×(-4)=-8.故选B.
2.(2020吉林长春一模,8)如图,点A,B分别在反比例函数y= (x>0),y= (x<0)的图象上.若OA⊥OB, =2,则a的值为 ( ) A.-4 B.4 C.-2 D.2
答案 A 过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,则∠AMO=∠BNO=90°,∴∠AOM+∠OAM= 90°.∵OA⊥OB,∴∠AOB=90°,∴∠AOM+∠BON=90°,∴∠OAM=∠BON,∴△AOM∽△OBN.∵点A,B分别在反比例函数y= (x>0),y= (x<0)的图象上,∴S△AOM∶S△BON=1∶(-a),∴AO∶BO=1∶ .∵OB∶OA=2,∴ =2,∴a=-4,故选A.
3.(2019辽宁铁岭一模,8)如图,点A是反比例函数y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y=- 的图象于点B,以AB为边作▱ABCD,其中C、D在x轴上,则S▱ABCD= ( )A.2 B.3 C.4 D.5
答案 D 设点A的纵坐标是b(b>0),则点B的纵坐标也是b.把y=b代入y= ,得b= ,则x= ,故点A的横坐标是 ;同理可得点B的横坐标是- .则AB= - = .则S▱ABCD= ×b=5.故选D.
4.(2019云南昆明官渡一模,14)如图,点A在反比例函数y= (x<0)的图象上,连接OA,分别以点O和点A为圆心,大于 AO的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为 ( ) A.-6 B.6 C.-2 D.-3
答案 A 如图,过A作AE⊥x轴于E,
依据作图可得,直线BC垂直平分线段AO,∴AD=OD,∴∠AOD=∠OAD=30°,∴∠ADE=60°,∴ED= AD= OD.∴S△AOE= S△AOD=3.∵点A在反比例函数y= (x<0)的图象上,∴ |k|=3,解得k=±6,又知k<0,∴k=-6,故选A.
二、填空题(每小题3分,共9分)5.(2020海南琼海一模,15)如图,在平面直角坐标系中,O为坐标原点,▱ABCD的边AB在x轴上,顶点D在y轴 的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与 BC交于点F.若y= (k≠0)的图象经过点C,且S△BEF=1,则k的值为 .
6.(2019云南昆明盘龙一模,6)过双曲线y= (k>0)上的动点A作AB⊥x轴于点B,P是直线AB上的点,且满足AP=2AB,过点P作x轴的平行线交此双曲线于点C.如果△APC的面积为8,则k的值是 .
7.(2018辽宁鞍山铁西3月模拟,14)如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2 CD,DB的延长线交y轴于点E,函数y= (k>0)的图象经过点A,若S△BCE=2,则k= .
8.(2020四川巴中5月模拟,24)如图,直线y=-x+b与反比例函数y= 的图象相交于A(1,4),B(4,n)两点,延长AO交反比例函数的图象另一支于点C,连接OB.(1)求k和b的值;(2)根据图象直接写出 -(-x+b)>0的解集;(3)在y轴上是否存在一点P,使得S△PAC= S△AOB?若存在,请求出点P的坐标;若不存在,请说明理由.
解析 (1)将(1,4)分别代入y=-x+b和y= ,得4=-1+b,4= ,解得b=5,k=4.(2) -(-x+5)>0可化为 >-x+5,即求反比例函数图象在一次函数图象上方时对应x的取值范围,由题图知 -(-x+5)>0的解集为x>4或0
9.(2020广西崇左江州一模,21)如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B (0,2),并与y= 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.(1)求一次函数与反比例函数的解析式;(2)若点C'是点C关于y轴的对称点,连接AC',BC',请求出△ABC'的面积.
解析 (1)∵直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),∴ 解得 ∴一次函数的解析式为y= x+2.∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4.∴C(3,4).∵点C在反比例函数y= 的图象上,∴k2=3×4=12.∴反比例函数的解析式为y= .(2)∵点C'是点C(3,4)关于y轴的对称点,∴C'(-3,4).又A(-3,0),∴AC'⊥AO.
∴S△ABC'=S梯形AOBC'-S△ABO= ×(2+4)×3- ×3×2=6.
10.(2019四川宜宾翠屏一诊,22)如图,直线y=kx+2与x轴,y轴分别交于点A(-1,0)和点B,与反比例函数y= 的图象在第一象限内交于点C(1,n).(1)求一次函数y=kx+2与反比例函数y= 的表达式;(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y= 交于P、Q两点,且PQ=2QD,求点D的坐标.
解析 (1)把(-1,0)代入y=kx+2,得-k+2=0,解得k=2,∴一次函数解析式为y=2x+2.把(1,n)代入y=2x+2,得n=4,∴C(1,4),把(1,4)代入y= ,得m=1×4=4,∴反比例函数解析式为y= .(2)∵PD∥y轴,D(a,0),∴P(a,2a+2),Q ,∵PQ=2QD,∴2a+2- =2× ,整理得a2+a-6=0,解得a1=2,a2=-3(舍去),经检验,a=2为原分式方程的解,且符合题意,∴D(2,0).
11.(2019云南昆明五华模拟,20)已知反比例函数y= (a为常数)的图象经过点B(-4,2).(1)求a的值;(2)如图,过点B作直线AB与函数y= 的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.
解析 (1)将(-4,2)代入y= ,得2= ,解得a=-12.(2)∵a=-12,∴反比例函数解析式为y=- ,分别过点B、A作x轴的垂线,垂足分别为点D、E,则BD=2.∵AB=3BC,∴ = .由作图知BD∥AE,∴△BCD∽△ACE,∴ = ,即 = ,∴AE=8.把y=8代入y=- ,得x=-1.∴A(-1,8).设直线AB的解析式为y=kx+b(k≠0),把(-1,8),(-4,2)代入解析式得, 解得 ∴直线AB的解析式为y=2x+10,当y=0时,2x+10=0,解得x=-5,∴C(-5,0),
中考数学一轮复习精品课件专题3.3 反比例函数(含答案): 这是一份中考数学一轮复习精品课件专题3.3 反比例函数(含答案),共4页。PPT课件主要包含了图象与性质,K的几何意义,与一次函数的综合,与几何图形的综合,取值范围,方法指导等内容,欢迎下载使用。
中考数学一轮复习知识点梳理+提升训练精品课件专题3.3《反比例函数》(含答案): 这是一份中考数学一轮复习知识点梳理+提升训练精品课件专题3.3《反比例函数》(含答案),共37页。PPT课件主要包含了图象与性质,K的几何意义,与一次函数的综合,与几何图形的综合,取值范围,方法指导等内容,欢迎下载使用。
中考一轮复习反比例函数课件: 这是一份中考一轮复习反比例函数课件,共33页。PPT课件主要包含了基础知识梳理,双曲线,比一比,面积性质一,想一想,面积性质二,y3x-1,y2x2,y3x,xy-2等内容,欢迎下载使用。












