2019-2020学年某校初三（上）12月阶段性测试数学试卷

这是一份2019-2020学年某校初三（上）12月阶段性测试数学试卷，共20页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。


1. 方程3x2−8x−10=0的二次项系数和一次项系数分别可以为( )
A.3和8B.3和−8C.3和−10D.3和10

2. 在一个不透明的袋子中装有6个小球，这些球除颜色外均相同，其中红球有2个，那么从袋子中随机摸出一个球，这个球是红球的概率为( )
A.12B.13C.14D.16

3. 抛物线y=−x2−4x+5 的顶点坐标为（ ）
A.(2, 1)B.(2, 9)C.(−2, −1)D.(−2, 9)

4. 对于反比例函数y=−2x，下列说法不正确的是( )
A.图象分布在第二、四象限
B.当x>0时，y随x的增大而增大
C.图象经过点(1, −2)
D.若点A(x1, y1)，B(x2, y2)都在图象上，且x1
5. 把抛物线y=2x2先向右平移3个单位长度，再向上平移4个单位长度，所得抛物线的解析式为( )
A.y=(x−3)2+4B.y=2(x+3)2−4
C.y=2(x−3)2+4D.y=2(x−3)2−4

6. 如图，四边形ABCD内接于⊙O，则∠1的度数为( )

A.120∘B.135∘C.140∘D.150∘

7. 已知等边三角形的内切圆半径为r，外接圆半径为R，边长为a，则r:R:a等于( )
A.1:2:3B.2:3:4C.1:3:2D.1:2:23

8. 如图，圆锥的底面半径OB长为3cm，母线AB长为8cm，则这个圆锥侧面展开图的圆心角α度数为( )

A.120∘B.135∘C.140∘D.150∘

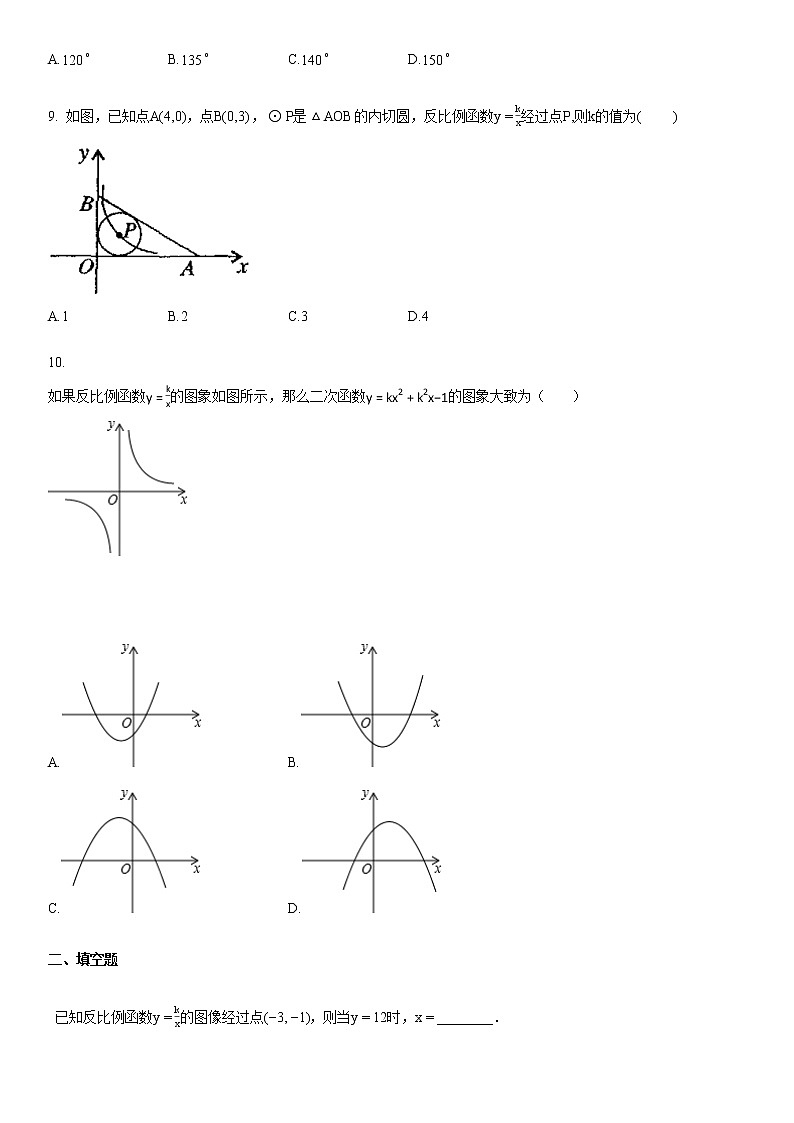
9. 如图，已知点A(4,0)，点B(0,3)，⊙P是△AOB的内切圆，反比例函数y=kx经过点P,则k的值为( )

A.1B.2C.3D.4

10.
如果反比例函数y=kx的图象如图所示，那么二次函数y=kx2+k2x−1的图象大致为（ ）
A.B.
C.D.
二、填空题

已知反比例函数y=kx的图像经过点(−3, −1)，则当y=12时，x=________．

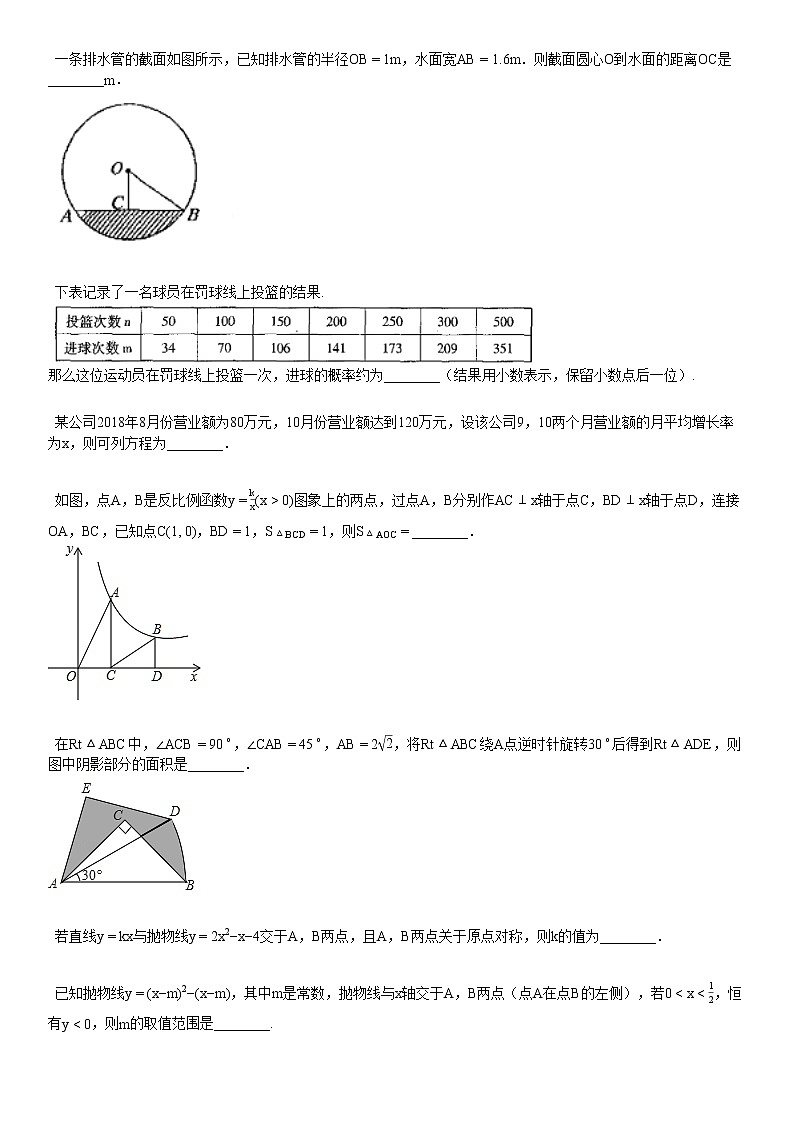
一条排水管的截面如图所示，已知排水管的半径OB=1m，水面宽AB=1.6m．则截面圆心O到水面的距离OC是________m．


下表记录了一名球员在罚球线上投篮的结果.
那么这位运动员在罚球线上投篮一次，进球的概率约为________（结果用小数表示，保留小数点后一位）.

某公司2018年8月份营业额为80万元，10月份营业额达到120万元，设该公司9，10两个月营业额的月平均增长率为x，则可列方程为________．

如图，点A，B是反比例函数y=kx(x>0)图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA，BC，已知点C(1, 0)，BD=1，S△BCD=1，则S△AOC=________．


在Rt△ABC中，∠ACB=90∘，∠CAB=45∘，AB=22，将Rt△ABC绕A点逆时针旋转30∘后得到Rt△ADE，则图中阴影部分的面积是________．


若直线y=kx与抛物线y=2x2−x−4交于A，B两点，且A，B两点关于原点对称，则k的值为________．

已知抛物线y=(x−m)2−(x−m)，其中m是常数，抛物线与x轴交于A，B两点（点A在点B的左侧），若0三、解答题

请用指定的方法解下列一元二次方程：
(1)配方法：x2−4x+1=0；

(2)公式法：2x2−22x+1=0.

不透明的口袋里装有红、黄、蓝三种颜色的球（除颜色外其余都相同）若干，其中红球有2个，黄球有1个，已知从中任意摸出一个是红球的概率为12．
(1)试求袋中蓝球的个数；

(2)第一次任意摸一个球（不放回），第二次再摸一个球，求这两个球都是红球的概率.(请用画树状图或列表法.)

如图，已知反比例函数 y=mx(m≠0) 的图象经过点 (1,5) ,一次函数y=−x+b 的图象经过反比例函数图象上的点 Q(−5,n).

(1)求反比例函数与一次函数的表达式；

(2)一次函数的图象分别与x轴、y轴交于A、B两点，与反比例函数图象的另一个交点为P,连结OP.求△AOP的面积.

如图，在Rt△ABC中，∠ACB=90∘,D是斜边AB上一点，以BD为直径的⊙O与AC相切于点E,交BC于点F.

(1)请你判断FE与ED 是否相等，并说明理由.

(2)若CE=8,BF=12，求⊙O 的半径的长.

某公司生产一种电子元件，经分析发现月销售量y(万个）与月份x(月）的关系为： y=x+12，(1≤x≤8，x为整数)，−x+28，(9≤x≤12，x为整数)， 每个产品的利润z（元）与月份x(月）的关系如下表：

(1)请你根据表格直接写出每个产品利润z(元）与月份x(月）的关系式；

(2)若月利润w(万元）=当月销售量y(万个）×当月每个产品的利润z(元），求月利润w(万元）与月份x(月）的关系式；

(3)几月份的利润最大，最大利润是多少？

如图，已知抛物线y=ax2+(1−2a)x−2(a>0)与x轴交于A，B两点（点A在点B左边），与y轴交于C点，直线l交x轴、y轴的正半轴分别于E，D点，OE=4,∠OED=45∘，直线l与抛物线交于M，N两点.

(1)直接写出直线l的解析式；

(2)当a(a>0)变化时，指出A，B，C三个点中的定点和动点，并说明理由；

(3)在直线l上是否存在定点P，使得无论a(a>0)怎么变化，PM⋅PN恒为定值？若存在，求出所有满足条件的点P的坐标，并说明点P是否在线段MN上；若不存在，请说明理由.
参考答案与试题解析
2019-2020学年湖北省荆州市某校初三（上）12月阶段性测试数学试卷
一、选择题
1.
【答案】
B
【考点】
一元二次方程的一般形式
【解析】
一元二次方程ax2+bx+c=0(a，b，c是常数且a≠0)的a、b、c分别是二次项系数、一次项系数、常数项．
【解答】
解：3x2−8x−10=0的二次项系数和一次项系数分别为3，−8.
故选B．
2.
【答案】
B
【考点】
概率公式
【解析】
此题暂无解析
【解答】
解：根据题意得P=26=13.
故选B.
3.
【答案】
D
【考点】
二次函数的性质
【解析】
此题暂无解析
【解答】
解：由y=−x2−4x+5，知y=−(x+2)2+9；
∴ 抛物线y=−x2−4x+5的顶点坐标为：(−2, 9)．
故选D．
4.
【答案】
D
【考点】
反比例函数图象上点的坐标特征
反比例函数的性质
【解析】
根据反比例函数图象的性质对各选项分析判断后利用排除法求解．
【解答】
解：A、k=−2<0，∴ 它的图象在第二、四象限，故本选项正确；
B、k=−2<0，当x>0时，y随x的增大而增大，故本选项正确；
C、∵ −21=−2，∴ 点(1, −2)在它的图象上，故本选项正确；
D、点A(x1, y1)，B(x2，y2)都在反比例函数y=−2x的图象上，
若x1故选D.
5.
【答案】
C
【考点】
二次函数图象与几何变换
【解析】
此题暂无解析
【解答】
解：抛物线y=2x2的顶点坐标为(0, 0)，
∵ 向右平移3个单位，再向上平移4个单位，
∴ 平移后的抛物线的顶点坐标为(3, 4)，
∴ 得到的抛物线解析式是y=2(x−3)2+4．
故选C.
6.
【答案】
C
【考点】
圆周角定理
圆内接四边形的性质
【解析】
此题暂无解析
【解答】
解：由题意得∠BCD=180∘−70∘=110∘，
∠BAD=180∘−110∘=70∘，
则∠1=2∠BAD=140∘.
故选C.
7.
【答案】
D
【考点】
正多边形和圆
【解析】
利用正三角形的边长与它的内切圆和外接圆的半径之间的关系求解．
【解答】
解：等边三角形的一边上的高的13倍为它的内切圆的半径r，
等边三角形的一边上的高的23倍为它的外接圆的半径R，
而高又为边长a的32倍，
∴ r:R:a=1:2:23．
故选D．
8.
【答案】
B
【考点】
弧长的计算
圆心角、弧、弦的关系
【解析】
此题暂无解析
【解答】
解：圆锥底面周长=2×3π=6π，
∴ 扇形的圆心角α=6π×180∘÷8π=135​∘．
故选B.
9.
【答案】
A
【考点】
三角形的内切圆与内心
勾股定理
待定系数法求反比例函数解析式
【解析】
此题暂无解析
【解答】
解：设内切圆半径为r，AB=AO2+OB2=5,
则S△AOB=S△AOP+S△BOP+S△ABP,
即12⋅AO⋅OB=12AO⋅r+12⋅OB⋅r+12⋅AB⋅r,
解得r=1，
∴ P(1,1)，
∴ k=1⋅1=1.
故选A.
10.
【答案】
A
【考点】
二次函数的图象
反比例函数的图象
【解析】
根据反比例函数图象得出k的符号，再利用k的符号判断抛物线的开口方向，对称轴，选择正确答案．
【解答】
解：根据反比例函数图象可知k>0，
由y=kx2+k2x−1 知，
二次函数开口向上，且对称轴x=−k2<0，在y轴左侧．
故选A．
二、填空题
【答案】
14
【考点】
待定系数法求反比例函数解析式
【解析】
此题暂无解析
【解答】
解：∵ 反比例函数y=kx的图像经过点(−3, −1)，
∴ −1=k−3，解得k=3，
∴ 反比例函数的解析式为y=3x，
∴ 当y=12时，12=3x,
解得x=14.
故答案为：14.
【答案】
0.6
【考点】
垂径定理的应用
勾股定理
【解析】
先根据垂径定理得出AB=2BC，再根据勾股定理求出BC的长，进而可得出答案．
【解答】
解：∵ OC⊥AB，AB=1.6cm，
∴ BC=0.8m,
在Rt△OBC中，由勾股定理得，
OC=OB2−BC2=12−0.82=0.6m，
则圆心O到水面的距离0.6m．
故答案为：0.6．
【答案】
0.7
【考点】
利用频率估计概率
【解析】
此题暂无解析
【解答】
解：由记录表可知每一组投中次数和投篮次数的比值分别为：
0.68；0.7；0.706；0.705；0.692；0.696；0.702，
随着投篮次数越来越大，频率逐渐稳定在0.7附近，
由此可估计这位同学投篮一次，投中的概率约是0.7.
故答案为：0.7．
【答案】
80(1+x)2=120
【考点】
由实际问题抽象出一元二次方程
【解析】
．
【解答】
解：设平均每月的增长率为x，
根据题意可得：80(1+x)2=120．
故答案为：80(1+x)2=120．
【答案】
32
【考点】
三角形的面积
待定系数法求反比例函数解析式
反比例函数系数k的几何意义
【解析】
由三角形BCD为直角三角形，根据已知面积与BD的长求出CD的长，由OC+CD求出OD的长，确定出B的坐标，代入反比例解析式求出k的值，利用反比例函数k的几何意义求出三角形AOC面积即可．
【解答】
解：∵ BD⊥CD，BD=1，
∴ S△BCD=12BD⋅CD=1，即CD=2，
∵ C(1, 0)，即OC=1，
∴ OD=OC+CD=1+2=3，
∴ B(3,1)，
代入反比例解析式得：k=3，即y=3x，
则S△AOC=32.
故答案为：32.
【答案】
2π3
【考点】
扇形面积的计算
旋转的性质
等腰直角三角形
【解析】
先根据勾股定理得到AB=22，再根据扇形的面积公式计算出S扇形ABD，由旋转的性质得到Rt△ADE≅Rt△ACB，于是S阴影部分=S△ADE+S扇形ABD−S△ABC=S扇形ABD．
【解答】
解：∵ ∠ACB=90∘，AB=22，
∴ S扇形ABD=30π⋅(22)2360=2π3．
又∵ Rt△ABC绕A点逆时针旋转30∘后得到Rt△ADE，
∴ Rt△ADE≅Rt△ABC，
∴ S阴影部分=S△ADE+S扇形ABD−S△ABC=S扇形ABD=2π3．
故答案为：2π3.
【答案】
−1
【考点】
关于原点对称的点的坐标
根与系数的关系
【解析】
根据两交点关于原点对称，可得k的值，根据抛物线的顶点坐标在y=x上，可得关于a的方程，根据解方程，可得答案．
【解答】
解：∵ 直线y=kx与抛物线y=2x2−x−4交于A，B两点，
∴ A，B两点的纵坐标满足kx=2x2−x−4，
即2x2−(1+k)x−4=0．
∵ A，B两点关于原点对称，
∴ 0=xA+xB=k+12，
∴ k=−1．
故答案为：−1.
【答案】
−12≤m≤0
【考点】
抛物线与x轴的交点
【解析】
此题暂无解析
【解答】
解：由题意知y=(x−m−1)(x−m)，令y=0，
解得x1=m，x2=m+1，因为点A在点B的左侧，
所以A(m,0)，B(m+1,0)，
又因为0所以m≤0，m+1≥12，
解得，−12≤m≤0.
故答案为：−12≤m≤0.
三、解答题
【答案】
解：(1)x2−4x+1=0，
移项，x2−4x=−1，
两边同时+4，x2−4x+4=3，
配方，(x−2)2=3，
开方，x−2=±3，
解得，x1=2+3，x2=2−3；
(2)2x2−22x+1=0，
Δ=b2−4ac=(−22)2−4×2×1=0，
则x1=x2=−b±Δ2a=224=22.
【考点】
解一元二次方程-公式法
解一元二次方程-配方法
【解析】
此题暂无解析
【解答】
解：(1)x2−4x+1=0，
移项，x2−4x=−1，
两边同时+4，x2−4x+4=3，
配方，(x−2)2=3，
开方，x−2=±3，
解得，x1=2+3，x2=2−3；
(2)2x2−22x+1=0，
Δ=b2−4ac=(−22)2−4×2×1=0，
则x1=x2=−b±Δ2a=224=22.
【答案】
解：(1)设袋中蓝球有x个，
则由题意得22+1+x=12，
解得，x=1.
经检验x=1是原方程的解.
所以袋中有蓝球1个.
(2)作出树状图如下：
所以两次摸到都是红球的概率P=212=16．
【考点】
列表法与树状图法
概率公式
【解析】
（1）考查了概率中的求法，解题时注意采用方程的方法比较简单；
（2）采用列表法或树状图法，解题时要注意是放回实验还是不放回实验．
【解答】
解：(1)设袋中蓝球有x个，
则由题意得22+1+x=12，
解得，x=1.
经检验x=1是原方程的解.
所以袋中有蓝球1个.
(2)作出树状图如下：
所以两次摸到都是红球的概率P=212=16．
【答案】
解：(1)将(1,5)代入y=mx中得m=5，∴ y=5x，
则Q(−5，−1)，
将Q代入y=−x+b得：b=−6,
∴ y=−x−6.
(2)当y=0时，0=−x−6，
x=−6，
∴ A=(−6,0),
当x=0时，y=−6，
∴ B=(0,−6),
−x−6=5x，
解得：x1=−1,x2=−5,
当x=−1时，y=−5，
∴ P(−1,−5),
过点P垂直于y轴于点N,
∵ OA=6，OB=6,PN=1,
∴ S△AOP=S△AOB−SOPB
=6⋅6⋅12−6×1×12
=18−3
=15.
【考点】
一次函数图象上点的坐标特点
待定系数法求一次函数解析式
三角形的面积
反比例函数综合题
待定系数法求反比例函数解析式
【解析】
此题暂无解析
【解答】
解：(1)将(1,5)代入y=mx中得m=5，∴ y=5x，
则Q(−5，−1)，
将Q代入y=−x+b得：b=−6,
∴ y=−x−6.
(2)当y=0时，0=−x−6，
x=−6，
∴ A=(−6,0),
当x=0时，y=−6，
∴ B=(0,−6),
−x−6=5x，
解得：x1=−1,x2=−5,
当x=−1时，y=−5，
∴ P(−1,−5),
过点P垂直于y轴于点N,
∵ OA=6，OB=6,PN=1,
∴ S△AOP=S△AOB−SOPB
=6⋅6⋅12−6×1×12
=18−3
=15.
【答案】
解：(1)连接OE，如图：
则OE⊥CA，
∵ ∠BCA=90∘，
∴ BC//OE，
∴ ∠CBE=∠OEB，
∵ OB=OE，
∴ ∠OEB=∠EBO，
∴ ∠CBE=∠EBO,
∴ FE=ED.
(2)连接FD，交OE于G，
∵ FE=ED，
∴ OE垂直平分FD，
∴ ∠EGF=∠GEC=∠FCE=90∘，
∴ 四边形FCEG为矩形，
∴ FG=CE=8，FD=16,
∠BFD=∠CFD=90∘，
在Rt△BFD中，
BD=162+122=20，
∴ OD=BD2=10.
【考点】
圆周角定理
圆心角、弧、弦的关系
矩形的判定与性质
【解析】
此题暂无解析
【解答】
解：(1)连接OE，如图：
则OE⊥CA，
∵ ∠BCA=90∘，
∴ BC//OE，
∴ ∠CBE=∠OEB，
∵ OB=OE，
∴ ∠OEB=∠EBO，
∴ ∠CBE=∠EBO,
∴ FE=ED.
(2)连接FD，交OE于G，
∵ FE=ED，
∴ OE垂直平分FD，
∴ ∠EGF=∠GEC=∠FCE=90∘，
∴ 四边形FCEG为矩形，
∴ FG=CE=8，FD=16,
∠BFD=∠CFD=90∘，
在Rt△BFD中，
BD=162+122=20，
∴ OD=BD2=10.
【答案】
解：(1)由表可知：
z=−x+28，(1≤x≤10，x为整数),18，(11≤x≤12，x为整数).
(2)当1≤x≤8时，w=(x+12)(−x+28)=−x2+16x+336；
当9≤x≤10时，w=(−x+28)(−x+28)=x2−56x+784；
当11≤x≤12时，w=(−x+28)×18=−18x+504，
综上，w=−x2+16x+336，(1≤x≤8)，x2−56x+784，(9≤x≤10)，−18x+504，(11≤x≤12).
(3)当1≤x≤8时，w=−x2+16x+336
=−(x−8)2+400，
∴当x=8时，w取得最大值，wmax=400；
当9≤x≤10时，w=(28−x)2，
∴当x=9时，w取得最大值，wmax=361；
当11≤x≤12时，w=−18x+504，
∴w随x的增大而减小，
∴当x=11时，w取得最大值，wmax=306.
综上：当x=8时，w取得最大值，wmax=400.
【考点】
一次函数的最值
根据实际问题列一次函数关系式
根据实际问题列二次函数关系式
二次函数的最值
【解析】
此题暂无解析
【解答】
解：(1)由表可知：
z=−x+28，(1≤x≤10，x为整数),18，(11≤x≤12，x为整数).
(2)当1≤x≤8时，w=(x+12)(−x+28)=−x2+16x+336；
当9≤x≤10时，w=(−x+28)(−x+28)=x2−56x+784；
当11≤x≤12时，w=(−x+28)×18=−18x+504，
综上，w=−x2+16x+336，(1≤x≤8)，x2−56x+784，(9≤x≤10)，−18x+504，(11≤x≤12).
(3)当1≤x≤8时，w=−x2+16x+336
=−(x−8)2+400，
∴当x=8时，w取得最大值，wmax=400；
当9≤x≤10时，w=(28−x)2，
∴当x=9时，w取得最大值，wmax=361；
当11≤x≤12时，w=−18x+504，
∴w随x的增大而减小，
∴当x=11时，w取得最大值，wmax=306.
综上：当x=8时，w取得最大值，wmax=400.
【答案】
解：(1)∵ OE=4,∠OED=45∘，
∴ OD=4，
∴ 直线l经过(4,0)，(0,4)，
设直线的解析式为：y=kx+b，
将(4,0)和(0,4)代入解析式中，
可得k=−1，b=4，
∴ 直线l的解析式为y=−x+4.
2对于抛物线：y=ax2+(1−2a)x−2(a>0)，
当y=0时，ax2+(1−2a)x−2=0，
Δ=(1−2a)2−4a×(−2)
=4a2−4a+1+8a
=4a2+4a+1
=(2a+1)2，
∴ x=2a−1±(2a+1)2a，
又a>0，
∴ x1=2，x2=−1a，
∴ −1a<0，
∴ B(2,0)，
当x=0时，y=−2，∴ C(0,−2)，
故A为动点，B，C为定点.
(3)在直线l上取一点P，过点M，P分别向x轴，y轴作垂线交于H点，如图：
设M(x1,y1)，N(x2,y2)，P(x0,y0),(x1PH//x轴，则∠HPM=∠OED=45∘，
∴ PH2+MH2=MP2，PH=MH，
∴PM=2PH=2|x0−x1|，
同理：PN=2|x0−x2|，
∴PM⋅PN=2|x0−x1||x0−x2|=2|(x0−x1)(x0−x2)|
=2|x02−(x1+x2)x0+x1x2|，
由y=ax2+(1−2a)x−2,y=−x+4,得ax2+(2−2a)x−6=0，
∴x1+x2=2−2a，x1⋅x2=−6a.
∴PM⋅PN=2|x02−(2−2a)x0−6a|=2|x02−2x0+2x0−6a|，
当a(a>0)变化时，要PM⋅PN为定值，
只有2x0−6=0，
∴x0=3，∴P(3,1)，
(3−x1)(3−x2)
=9−3(x1+x2)+x1x2
=9−3(2−2a)−6a=3>0,
x1≤3≤x2不可能，
所以P不在线段MN上.
【考点】
待定系数法求一次函数解析式
二次函数综合题
抛物线与x轴的交点
【解析】
此题暂无解析
【解答】
解：(1)∵ OE=4,∠OED=45∘，
∴ OD=4，
∴ 直线l经过(4,0)，(0,4)，
设直线的解析式为：y=kx+b，
将(4,0)和(0,4)代入解析式中，
可得k=−1，b=4，
∴ 直线l的解析式为y=−x+4.
2对于抛物线：y=ax2+(1−2a)x−2(a>0)，
当y=0时，ax2+(1−2a)x−2=0，
Δ=(1−2a)2−4a×(−2)
=4a2−4a+1+8a
=4a2+4a+1
=(2a+1)2，
∴ x=2a−1±(2a+1)2a，
又a>0，
∴ x1=2，x2=−1a，
∴ −1a<0，
∴ B(2,0)，
当x=0时，y=−2，∴ C(0,−2)，
故A为动点，B，C为定点.
(3)在直线l上取一点P，过点M，P分别向x轴，y轴作垂线交于H点，如图：
设M(x1,y1)，N(x2,y2)，P(x0,y0),(x1PH//x轴，则∠HPM=∠OED=45∘，
∴ PH2+MH2=MP2，PH=MH，
∴PM=2PH=2|x0−x1|，
同理：PN=2|x0−x2|，
∴PM⋅PN=2|x0−x1||x0−x2|=2|(x0−x1)(x0−x2)|
=2|x02−(x1+x2)x0+x1x2|，
由y=ax2+(1−2a)x−2,y=−x+4,得ax2+(2−2a)x−6=0，
∴x1+x2=2−2a，x1⋅x2=−6a.
∴PM⋅PN=2|x02−(2−2a)x0−6a|=2|x02−2x0+2x0−6a|，
当a(a>0)变化时，要PM⋅PN为定值，
只有2x0−6=0，
∴x0=3，∴P(3,1)，
(3−x1)(3−x2)
=9−3(x1+x2)+x1x2
=9−3(2−2a)−6a=3>0,
x1≤3≤x2不可能，
所以P不在线段MN上.