






- 28.1 锐角三角函数(2) 课件+教案 课件 11 次下载
- 28.1 锐角三角函数(4) 课件+教案 课件 11 次下载
- 28.2 解直角三角形(1) 课件+教案 课件 11 次下载
- 28.2 解直角三角形(2) 课件+教案 课件 12 次下载
- 28.2 解直角三角形(3) 课件+教案 课件 11 次下载
2021学年28.1 锐角三角函数优质课ppt课件
展开28.3锐角三角函数(3)
教学目标:
1、熟记30°,45°,60°角的三角函数值,并能根据这些值说出对应的锐角度数.
2、培养学生把实际问题转化为数学问题的能力.培养学生观察、比较、分析、概括的能力.
3、经历观察、操作、归纳等学习数学的过程,感受数学思考过程的合理性,感受数学说理的必要性、说理过程的严谨性,养成科学、严谨的学习态度.
教学重点
30°,45°,60°角的三角函数值.
教学难点
与特殊角的三角函数值有关的计算.
教学过程:
一、新知引入
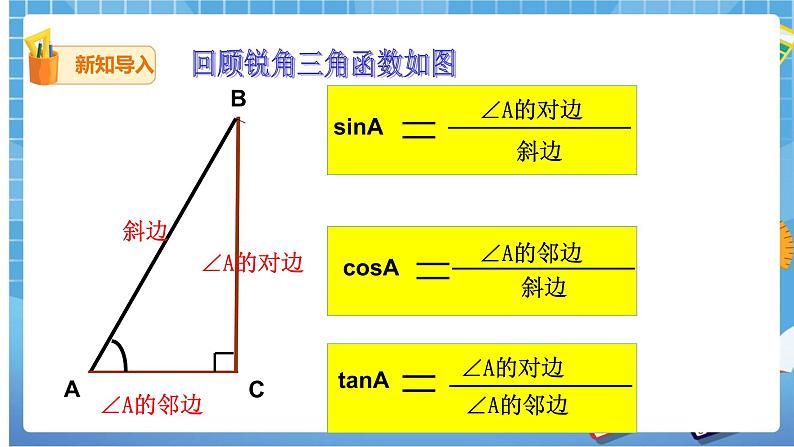
如图,在Rt△ABC中,∠C=90°.
(1)a,b,c三者之间的关系是________;
(2)sinA=________,cosA=________,tanA=________;
sinB=________,cosB=________,tanB=________.
(3)若∠A=30°,则=________.
二、共同探究,获取新知
探索30°,45°,60°角的三角函数值.
①观察一副三角尺,其中有几个锐角?它们分别等于多少度?
一副三角尺中有四个锐角,它们分别是30°,60°,45°,45°.
②sin30°等于多少呢?你是怎样得到的?与同伴交流.
③cos30°等于多少?tan30°呢?
cos30°==.tan30°===.
④我们求出了30°角的三个三角函数值,还有两个特殊角——45°,60°,它们的三角函数值分别是多少?你是如何得到的?
求60°角的三角函数值可以利用求30°角的三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边,利用上图,很容易求得sin60°==,cos60°==,tan60°==.
分析:我们一起来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.如图,设其中一条直角边为a,则另一条直角边也为a,斜边为a.由此可求得
sin45°===,cos45°===,
tan45°==1.
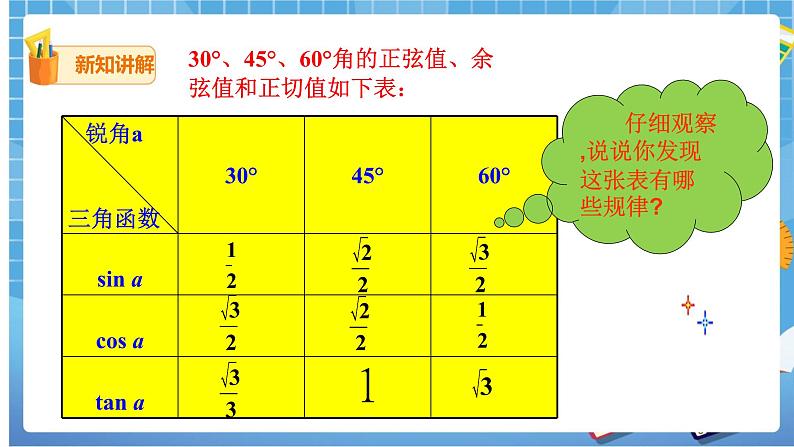
●归纳:课件出示:
三角函数 |
|
|
|
角度α | sinα | cosα | tanα |
30° | |||
45° | 1 | ||
60° |
规律:
①这个表格中的30°,45°,60°角的三角函数值需要熟记.另一方面,要能够根据30°,45°,60°角的三角函数值说出相应的锐角的大小.
②第一列,随着角度的增大,正弦值在逐渐增大.
③第二列,余弦值随角度的增大而减小.
师:第三列呢?
④第三列是30°,45°,60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.随着角度的增大,正切值也在增大.
三、例题讲解
例1 求下列各式的值:
(1)cos260°+sin260°; (2)
答案:(1)原式= 1 (1)原式= 0
●总结:有关特殊角的三角函数值的计算,先直接写出三角函数值,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
巩固练习:
1.sin45°的值是( D )
A. B.1 C. D.
2.已知α为等腰直角三角形的一个锐角,则cos α等于( B )
A. B. C. D.
3.计算:2sin60°+tan45°=___________.
4.Rt△ABC中,∠C=90°,cos A= ,则∠A=_30__ °.
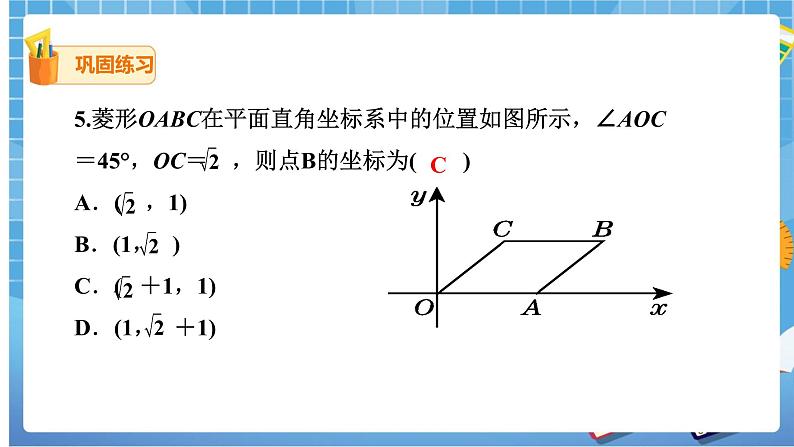
5.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B的坐标为(C )
A.(,1) B.(1,) C.(+1,1) D.(1,+1)
6.计算:(1)4sin300-cos450+tan600 (2)2cos 30°+tan 60°-2tan 45°·tan 60°.
解:(1)原式=1+3 (2)原式=0
根据一个锐角的特殊的三角函数值,也可以求出角的度数.
例2 (1)如图(1),在Rt△ABC中,∠C=90°,AB=,BC=,求∠A的度数;
(2)如图(2),AO是圆锥的高,OB是底面半径,AO=OB,求α的度数.
解:(1)在图(1)中,
∵sinA===,
∴∠A=45°.
(2)在图(2)中,
∵tanα===,
∴α=60°.
巩固练习:
1.已知α为锐角,且tan(90°-α)=,则α等于(B)。
A 30° B 60 ° C 45° D 75°
2.在△ABC中,∠A,∠B都是锐角,且sinA=,cos B=,则△ABC的形状是(B )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3.已知α,β均为锐角,且满足则α+β=________.(答案:750)
四、拓展提高
例3 已知∠A为锐角,sin A=,求∠A的其他三角函数值.
●总结:
(1)当A、B均为锐角时,若A≠B,则sinA≠sinB, cosA≠cosB,tanA≠tanB.
(2)sin2α+cos2α=1,tanα=
你能用得出的公式规律,重新解答例3吗?
解法二:(略)学生自主解答
巩固练习:
1.在Rt△ABC中,∠C=90°,下列式子不一定成立的是( )A
A.tan A= B.sin2 A+cos2 A=1
C.sin2 A+sin2 B=1 D.tan A·tan B=1
2.在Rt△ABC中,∠C=90°,若sin A=,则cos B的值是( )B
A. B. C. D.
3.如果α是锐角,且cosα=,那么sin(90°-α)的值等于( ) C
A. B. C. D.
4.直角三角形的斜边和一条直角边的比为25∶24,则其中最小的角的正切值为_____。(答案:)
5.如图,为测河两岸相对两电线杆A、B的距离,在距A点17米的C处(AC⊥AB)测得∠ACB=50°,则A、B间的距离为( )C
A. 17sin50°米 B. 17cos50°米 C. 17tan50°米 D. 34sin50°米
五、课堂小结
1.探索30°,45°,60°角的三角函数值.
sin30°= ,sin45°=,sin60°=;
cos30°= ,cos45°=,cos60°=;
tan30°= ,tan45°=1,tan60°=.
2.能进行含30°,45°,60°角的三角函数值的计算.
3.能根据30°,45°,60°角的三角函数值说出相应锐角的大小.
六、布置作业:教材67页练习1、2题
数学人教版28.1 锐角三角函数完整版ppt课件: 这是一份数学人教版28.1 锐角三角函数完整版ppt课件,共22页。PPT课件主要包含了三角函数包括哪些,另一条直角边长,解在图中,∴α60°,解方法①,方法②等内容,欢迎下载使用。
初中数学人教版九年级下册第二十八章 锐角三角函数28.1 锐角三角函数备课课件ppt: 这是一份初中数学人教版九年级下册第二十八章 锐角三角函数28.1 锐角三角函数备课课件ppt,共10页。PPT课件主要包含了预习导学,自学指导,自学检测,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级下册28.1 锐角三角函数说课课件ppt: 这是一份初中数学人教版九年级下册28.1 锐角三角函数说课课件ppt,文件包含281锐角三角函数3课件pptx、281锐角三角函数3教案doc等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。













