2021年北师大版数学九年级上册《图形的相似》期末复习卷（含答案）

2021年北师大版数学九年级上册

《图形的相似》期末复习卷

一、选择题

1.将式子ab=cd(a，b，c，d都不等于0)写成比例式，错误的是(　　)

A.=     B.=     C.=    D.=

2.在一张比例尺为1：5000000的地图上，甲、乙两地相距70毫米，此两地实际距离为（　　）

A.3.5千米     B.35千米       C.350千米     D.3500千米

3.用一个10倍的放大镜看一个15°的角，看到的角的度数为（    ）

A.150°          B.105°          C.15°          D.无法确定大小

4.如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C，直线DF分别交l1，l2，l3于点D，E，F，AC与DF相交于点G，且AG=2，GB=1，BC=5，则的值为(　　)

A.         B.2         C.         D.

5.下列说法中正确的是（     ）

A.两个直角三角形相似         B.两个等腰三角形相似

C.两个等边三角形相似                             D.两个锐角三角形相似

6.如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（　　）

A.a=b       B.a=2b      C.a=2b        D.a=4b

7.如果两个相似多边形的面积比为16：9，那么这两个相似多边形的相似比为（　　）

A.16：9        B.4：3           C.2：3         D.256：81

8.下图中四个阴影的三角形中与△ABC相似的是(　　)

A.   B.   C.     D.

9.两个相似三角形的最短边分别为5 cm和3 cm，他们的周长之差为12 cm，那么大三角形的周长为(　 　)

A.14 cm               B.16 cm      C.18 cm               D.30 cm

10.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为13，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点的坐标为(　　)

A.(3，2)    B.(3，1)    C.(2，2)    D.(4，2)

11.一个钢筋三角架的三边长分别为20 cm，50 cm，60 cm，现在要做一个和它相似的钢筋三角架，而只有长为30 cm和50 cm的两根钢筋，要求以其中的一根为一边，从另一根上截两段(允许有余料)作为另两边，则不同的截法有(　 　)

A.一种       B.两种      C.三种       D.四种或四种以上

12.如图，小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离)，在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米，A，B，C三点共线)，把一面镜子水平放置在平台上的点G处，测得CG=15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得EG=3米，小明身高EF=1.6米，则凉亭的高度AB约为(　 　)

A.8.5米       B.9米       C.9.5米       D.10米

二、填空题

13.已知=，则=________.

14.若两个相似多边形的面积比是16：25，则它们的周长比等于______.

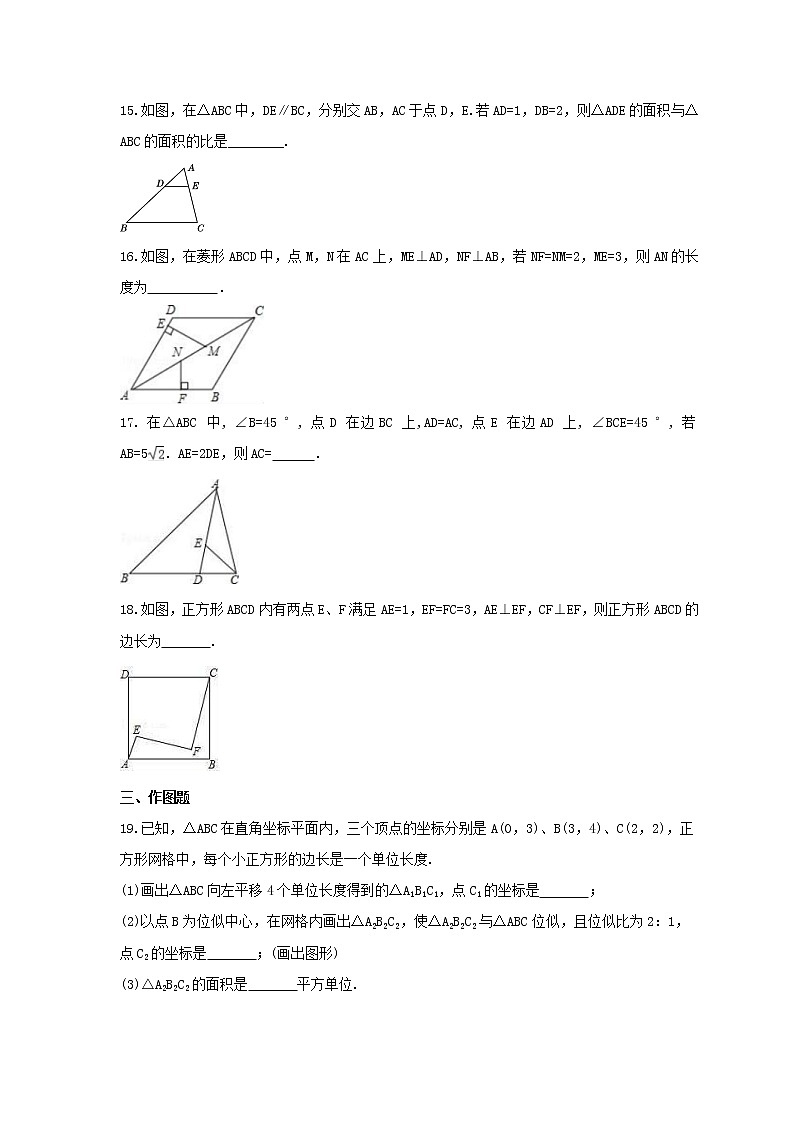
15.如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E.若AD=1，DB=2，则△ADE的面积与△ABC的面积的比是________.

16.如图，在菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB，若NF=NM=2，ME=3，则AN的长度为          ．

17.在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5．AE=2DE，则AC=      ．

18.如图，正方形ABCD内有两点E、F满足AE=1，EF=FC=3，AE⊥EF，CF⊥EF，则正方形ABCD的边长为　   　.

三、作图题

19.已知，△ABC在直角坐标平面内，三个顶点的坐标分别是A(0，3)、B(3，4)、C(2，2)，正方形网格中，每个小正方形的边长是一个单位长度.

(1)画出△ABC向左平移4个单位长度得到的△A1B1C1，点C1的坐标是　   　；

(2)以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是　   　；(画出图形)

(3)△A2B2C2的面积是　   　平方单位.

四、解答题

20.在比例尺为1：10000的地图上，有甲、乙两个相似三角形区域，其周长分别为10cm和15cm.

（1）求它们的面积比；

（2）若在地图上量得甲的面积为16cm2，则乙所表示的实际区域的面积是多少平方米？

21.如图，在离某建筑物CE4m处有一棵树AB，在某时刻，1.2m的竹竿FG垂直地面放置，影子GH长为2m，此时树的影子有一部分落在地面上，还有一部分落在建筑物的墙上，墙上的影子CD高为2 m，那么这棵树的高度是多少？

22.如图，在△ABC中，已知AB=AC，点D，E，B，C在同一条直线上，且AB2=BD·CE.

求证：△ABD∽△ECA.

23.周末，小华和小亮想用所学的数学知识测量家门前小河的宽.测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D，竖起标杆DE，使得点E与点C，A共线.

已知：CB⊥AD，ED⊥AD，测得BC=1 m，DE=1.5 m，BD=8.5 m.测量示意图如图所示.请根据相关测量信息，求河宽AB.

24.如图，在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中点，ED交AB的延长线于点F.

求证：AB·AF=AC·DF.

25.如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B.

(1) 求证：∠DFA=∠ECD；

(2) △ADF与△DEC相似吗？为什么？

(3) 若AB=4，AD=3，AE=3，求AF的长.

26.已知：如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于E，交BC边于F，分别连接AF和CE．

（1）求证：四边形AFCE是菱形；

（2）若AE=10cm，△ABF的面积为24cm2，求△ABF的周长；

（3）在线段AC上是否存在一点P，使得2AE2=AC•AP？若存在，请说明点P的位置，并予以证明；若不存在，请说明理由．

参考答案

1.答案为：D

2.答案为：C.

3.答案为：C.

4.答案为：D.

5.答案为：C

6.答案为：B；.

7.答案为：B

8.答案为：B.

9.答案为：D

10.答案为：A.

11.答案为：B.

12.答案为：A.

13.答案为：－.

14.答案为：4：5.

15.答案为：1:9

16.答案为4．

17.答案为：．

18.答案为：.

19.解：(1)如图，△A1B1C1即为所求，点C1的坐标是(﹣2，2)，

故答案为：(﹣2，2)；

(2)如图所示，△A2B2C2即为所求，点C2的坐标是(1，0)，故答案为：(1，0)；

(3)△A2B2C2的面积×(2+4)×6﹣×2×4﹣×2×4=10，故答案为：10；

20.解：（1）；

（2）∵，，∴，

又∵比例尺是1：1000，

∴.

21.解：延长AD，与地面交于点M，如图

由AM∥FH知∠AMB=∠FHG.

又因为AB⊥BG，FG⊥BG，DC⊥BG，

所以△ABM∽△DCM∽△FGH，所以==.[

因为CD=2 m，FG=1.2 m，GH=2 m，

所以=，解得CM= m.

因为BC=4 m，所以BM=BC＋CM=4＋=(m).

所以=，解得AB=4.4 m.

故这棵树的高度是4.4 m.

22.证明：∵AB=AC，∴∠ABC=∠ACB，

∴∠ABD=∠ACE.

∵AB2=BD·CE，

∴=，即=，

∴△ABD∽△ECA.

23.解：∵CB⊥AD，ED⊥AD，∴BC∥DE，

∴△ABC∽△ADE，

∴=，即=，

解得AB=17(m).

经检验，AB=17是原分式方程的解.

答：河宽AB的长为17 m.

24.证明：∵AD⊥BC，E是AC的中点，

∴DE=EC.

∴∠EDC=∠C.

∵∠BAC=∠ADC=90°，

 ∴∠BAD＋∠DAC=90°，∠DAC＋∠C=90°.

∴∠BAD=∠C.

∵∠BDF=∠EDC，∴∠BDF=∠BAD.

又∵∠F为公共角，

∴△BDF∽△DAF.∴=.

∵∠ADB=∠ADC=90°， ∠BAD=∠C，

∴△ABD∽△CAD.∴=.

∴=，

即AB·AF=AC·DF.

25.解：(1)证明：∵∠AFE=∠B，∠AFE＋∠DFA=180°，∠B＋∠ECD=180°，

∴∠DFA=∠ECD　

(2)△ADF∽△DEC.证明：

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠ADF=∠DEC，

∴△ADF∽△DEC　

(3)∵四边形ABCD是平行四边形，

∴AD∥BC，CD=AB=4，

又∵AE⊥BC，

∴AE⊥AD，

在Rt△ADE中，DE===6，

∵△ADF∽△DEC，

∴=，

∴=，AF=2

26.（1）证明：连接EF交AC于O，当顶点A与C重合时，折痕EF垂直平分AC，∴OA=OC，∠AOE=∠COF=90°∵在矩形ABCD中，AD∥BC，∴∠EAO=∠FCO，∴△AOE≌△COF（ASA）．∴OE=OF∴四边形AFCE是菱形．

（2）解：四边形AFCE是菱形，∴AF=AE=10．

设AB=x，BF=y，∵∠B=90，∴（x+y）2﹣2xy=100① 又∵S△ABF=24，∴0.5xy=24，则xy=48．②

由①、②得：（x+y）2=196∴x+y=14，x+y=﹣14（舍去）.∴△ABF的周长为x+y+AF=14+10=24．

（3）解：过E作EP⊥AD交AC于P，则P就是所求的点．

证明：由作法，∠AEP=90°，由（1）得：∠AOE=90°，又∠EAO=∠EAP，

∴△AOE∽△AEP，∴AE:AP=OA:AE，则AE2=AO•AP

∵四边形AFCE是菱形，∴AO=0.5AC，AE2=0.5AC•A.

∴2AE2=AC•AP即P的位置是：过E作EP⊥AD交AC于P．