数学冀教版10.4 一元一次不等式的应用图片课件ppt

这是一份数学冀教版10.4 一元一次不等式的应用图片课件ppt，文件包含104一元一次不等式的应用ppt、104一元一次不等式的应用doc等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

1.经历“实际问题抽象为不等式模型”的过程，从而学会用一元一次不等式解决实际问题.（重、难点）2.体会不等式是刻画现实世界中不等关系的一种有效的数学模型.
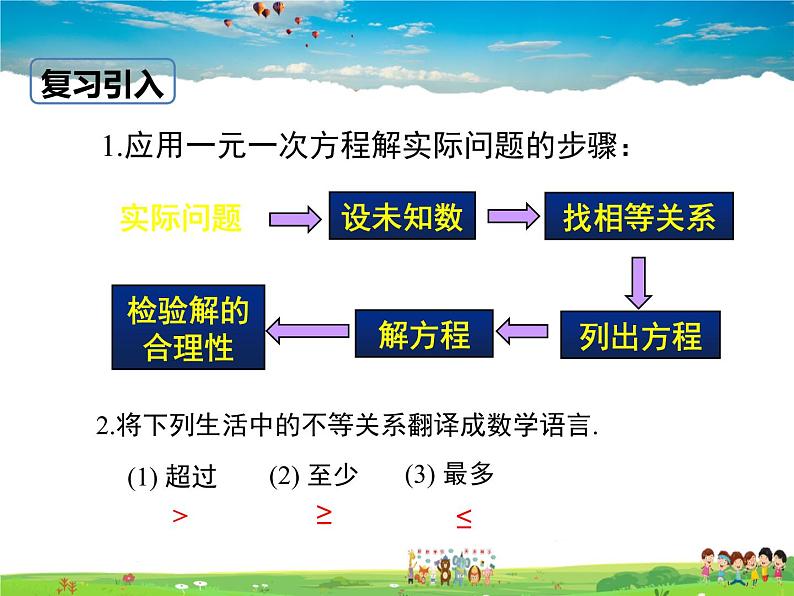
1.应用一元一次方程解实际问题的步骤：
2.将下列生活中的不等关系翻译成数学语言.
七年级(一)班的学生准备用500元，购买甲、乙两种图书共12套，送给老区的幼儿园小朋友.已知甲种图书每套45元，乙种图书每套40元.这些钱最多能买甲种图书多少套?
问题1： 设可购买甲种图书x套，则购买甲种图书用的钱为______元，购买乙种图书________套，购买乙种图书用的钱为________元.
问题2： 购买甲、乙两种图书所用钱数与500元有什么关系?
甲图书所用钱数 + 乙图书所用钱数 ≤ 500.
问题3： 你能用不等式把这种关系表示出来吗?
45x+40(12-x)≤ 500
问题4：解上面列出的不等式，并根据解集确定实际问题的答案.
解得x≤ 4，故最多购买甲图书4套.
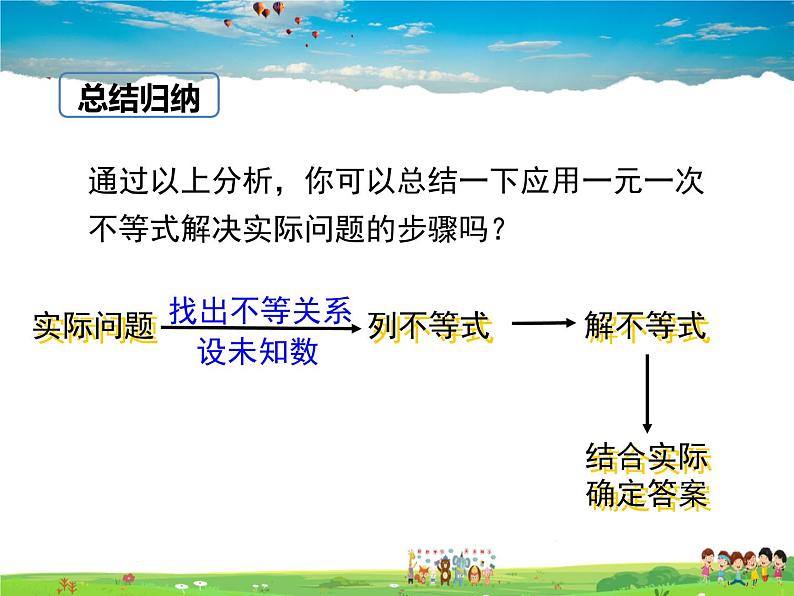
通过以上分析，你可以总结一下应用一元一次不等式解决实际问题的步骤吗？
例1 某商场为响应“家电下乡”的惠农政策，决定采购一批电冰箱，优惠销售给农民朋友. 商场从厂家直接购进甲、乙、丙三种不同型号的电冰箱共80台，其中，甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超过132000元，已知甲、乙、丙三种电冰箱每台的出厂价格分别为1200元，1600元，2000元. 那么该商场购进的乙种电冰箱至少为多少台？
解析：题中的等量关系， 甲冰箱数 + 乙冰箱数 + 丙冰箱数 = 80 甲冰箱数 = 2×乙冰箱数 题中的不等关系， 1200×甲冰箱数+1600×乙冰箱数+ 2000×丙冰箱数≤132000
根据题意列不等式，得 1200×2x+1600x+2000(80-3x)≤132000. 解这个不等式，得 x≥14.答：至少购进乙种电冰箱14台.
解：设购买乙种电冰箱x台，则购买甲种电冰箱是2x台，丙种电冰箱是(80-3x)台.
例2 某班几个同学合影留念，每人交0.7元.已知一张彩色底片0.68元，扩印一张相片0.5元，每人分一张，在将收来的钱尽量用掉的前提下，这张相片上的同学最少有几人？
解析：题中的等量关系，收来的钱=0.7元×人数花去的钱=0.68元+0.5元×人数题中的不等关系， 花去的钱≤收来的钱
解：设这张相片上的同学有x人. 根据题意列不等式，得 0.7x≥0.68+0.5x. 解这个不等式，得 x≥3.4. 因为x为正整数，所以x至少为4.答：这张相片上的同学至少有4人.
方法归纳：在用不等式解决实际问题时，当求出解集后，还要根据问题的实际意义确定问题的解.
例3 三个连续正整数的和小于39，这样的正整数中，最大一组的和是多少？
解：设三个连续正整数分别为x﹣1，x，x+1. 根据题意列不等式，得 (x﹣1)+x+(x+1)＜39. 解这个不等式，得 x＜13. 所以当x=12时，三个连续整数的和最大. 三个连续整数的和为：11+12+13=36.
练一练：1.一堆玩具分给若干个小朋友，若每人分3件，则剩余4件，若前面每人分4件，则最后一人得到的玩具最多3件，问小朋友的人数至少有几人？
解析：第一次分配中的等量关系， 玩具总数 = 3×人数 + 剩余玩具数 第二次分配中的不等关系 玩具总数 - 前面的人数×4≤3
解：设小朋友的人数为x，则玩具总数为3x+4. 据题意列不等式，得 (3x+4) -4(x-1)≤3 解得 x≥5.答：小朋友至少有5人.
2. 某商店购进一批水果，运输过程中质量损失10%，假设不计商店的其他费用．（1）如果商店在进价的基础上提高10%作为售价，则该商店的盈亏情况是_________；（填“盈”、“亏”或“不盈不亏”）
解析：利润=售价﹣进价. 设进价为a. 依题意，得 利润 = (1﹣10%)×(1+10%)a﹣a 即 利润=﹣0.01a.
（2）若该商店想要至少获得20%的利润，则这种水果的售价在原进价的基础上至少提高多少？
解：设水果的售价在原进价的基础上提高x. 据题意列不等式，得 (1﹣10%)(1+x) ≥ (1+20%) 解得 答：水果得售价在原进价的基础上至少提高 ．
1. 某次知识竞赛共20道题，每一题答对得10分，答错或不答都扣5分，小英得分不低于90分．设她答对了x道题，则根据题意可列出不等式为（　　） A．10x + 5(20﹣x) ≥ 90 B．10x﹣5(20﹣x) ＞90 C．10x﹣(20﹣x) ≥ 90 D．10x﹣(20﹣x) ＞90
2. 某工程队计划在10天修路6千米，施工前2天修完1.2千米，计划发生变化，准备提前2天完成修路任务，则以后几天内平均每天至少要修________千米.
解析：计划改变时，还剩6-1.2=4.8千米未修； 计划改变时，还剩10-2-2=4天时间； 则题中的不等关系为 剩余天数×计划改变后每天修路数≥剩余路数 设以后几天平均每天修路x千米. 根据题意得 (10﹣2﹣2)x≥6﹣1.2. 解得 x≥0.8
3. 在纪念中国抗日战争胜利71周年之际，某公司决定组织员工观看抗日战争题材的影片，门票有甲乙两种，甲种票比乙种票每张贵6元；买甲种票10张，乙种票15张共用去660元．（1）求甲、乙两种门票每张各多少元？
解：设乙种门票每张x元，则甲种门票每张(x+6)元. 根据题意得 10(x+6)+15x = 660， 解得 x = 24.答：甲、乙两种门票每张各30元、24元.
（2）如果公司准备购买35张门票且购票费用不超过1000元，那么最多可购买多少张甲种票？
解：设可购买y张甲种票，则购买(35﹣y)张乙种票. 根据题意得 30y+24(35﹣y)≤1000， 解得 .答：最多可购买26张甲种票.