2021年河南省南阳市镇平县中考数学模拟试卷（一） 解析版

这是一份2021年河南省南阳市镇平县中考数学模拟试卷（一） 解析版，共30页。试卷主要包含了选择题等内容，欢迎下载使用。
2021年河南省南阳市镇平县中考数学模拟试卷（一）
一、选择题（每小题3分，共30分）
1．（3分）下列四个数：﹣2，1，﹣，π，其中最小的数是（　　）
A．﹣2 B．1 C．﹣ D．π
2．（3分）舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约499.5亿千克，这个数用科学记数法应表示为（　　）
A．4.995×1011 B．49.95×1010
C．0.4995×1011 D．4.995×1010
3．（3分）六个大小一样的正方体搭成的几何体如图所示，则关于它的视图说法正确的是（　　）

A．正视图的面积最大 B．俯视图的面积最大
C．左视图的面积最大 D．三个视图的面积一样大
4．（3分）下列调查方式，你认为最合适的是（　　）
A．了解北京市每天的流动人口数，采用抽样调查方式
B．旅客上飞机前的安检，采用抽样调查方式
C．了解北京市居民“一带一路”期间的出行方式，采用全面调查方式
D．日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式
5．（3分）如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（　　）

A．30° B．40° C．50° D．60°
6．（3分）下列一元二次方程中，没有实数根的是（　　）
A．x2﹣2x＝0 B．2x2﹣4x+3＝0 C．x2+4x﹣1＝0 D．3x2＝5x﹣2
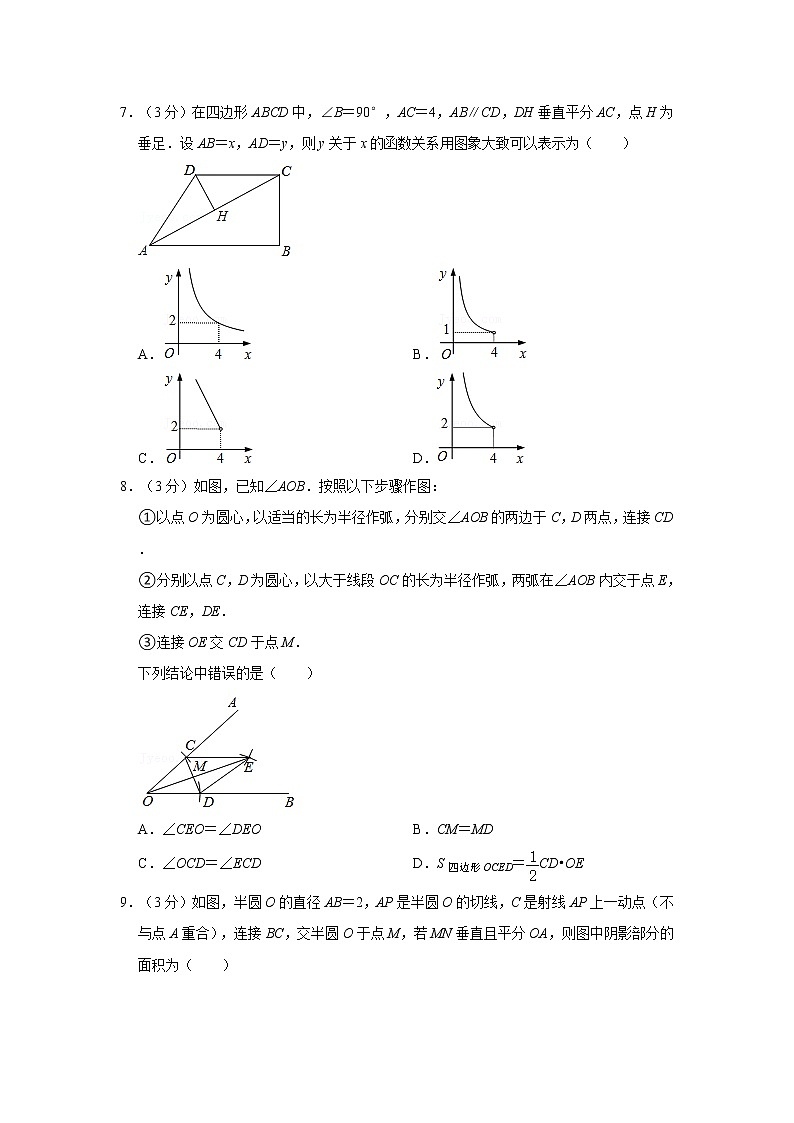
7．（3分）在四边形ABCD中，∠B＝90°，AC＝4，AB∥CD，DH垂直平分AC，点H为垂足．设AB＝x，AD＝y，则y关于x的函数关系用图象大致可以表示为（　　）

A． B．
C． D．
8．（3分）如图，已知∠AOB．按照以下步骤作图：
①以点O为圆心，以适当的长为半径作弧，分别交∠AOB的两边于C，D两点，连接CD．
②分别以点C，D为圆心，以大于线段OC的长为半径作弧，两弧在∠AOB内交于点E，连接CE，DE．
③连接OE交CD于点M．
下列结论中错误的是（　　）

A．∠CEO＝∠DEO B．CM＝MD
C．∠OCD＝∠ECD D．S四边形OCED＝CD•OE
9．（3分）如图，半圆O的直径AB＝2，AP是半圆O的切线，C是射线AP上一动点（不与点A重合），连接BC，交半圆O于点M，若MN垂直且平分OA，则图中阴影部分的面积为（　　）

A． B． C． D．
10．（3分）如图，在平面直角坐标系xOy中，A（4，0），B（0，3），C（4，3），I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I′的坐标为（　　）

A．（﹣2，3） B．（﹣3，2） C．（3，﹣2） D．（2，﹣3）
二.填空题（每小题3分，共15分）
11．（3分）设a＝﹣1，a在两个相邻整数之间，则这两个整数是　 　．
12．（3分）已知x＝3满足关于a的不等式，则这个不等式的解是 　 　．
13．（3分）三张背面完全相同的数字牌，它们的正面分别印有数字1，2，3，将它们背面朝上，洗匀后随机抽取一张，记录牌上的数字并把牌放回，再重复这样的步骤，得到数字a，b，则a≥b的概率是 　 　．
14．（3分）如图1，△ABC为直角三角形，∠C＝90°，四边形DEFG为矩形，且点C、B、E、F在同一条直线上，点B与点E重合，AC＝DE．Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移，当点C与点F重合时停止．设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2，运动时间xs．反映ycm2与xs之间函数关系的大致图象如图2，则矩形DEFG的面积为 　 　cm2．

15．（3分）如图，已知Rt△ABC中，∠B＝90°，∠A＝60°，AC＝2+4，点M、N分别在线段AC、AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为　 　．

三.解答题（共2小题，满分17分）
16．（8分）先化简，再求值：（+a﹣3）÷，其中a为不等式组的整数解．
17．（9分）今年春节，新型冠状病毒感染的肺炎疫情牵动着全国人民的心，为了提高意识，共克时艰，共渡难关，綦江区某校开展了“全民行动•共同抗疫”的自我防护知识网上答题竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100），下面给出了部分信息：
七年级10名学生的竞赛成绩是：90，80，90，86，99，96，96，100，89，82
八年级10名学生的竞赛成绩在C组中的数据是：94，90，94
七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
90
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：
（1）直接写出上述图表中a，b，c的值．
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）．
（3）该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？


18．（9分）如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G在同一直线上，cos80°≈0.018，sin80°≈0.98，≈1.414），此时小强头部E点与地面DK的距离是多少？

19．（9分）商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为p＝，且其日销售量y（kg）与时间t（天）的关系如表：
时间t（天）
1
3
6
10
20
40
…
日销售量y（kg）
118
114
108
100
80
40
…
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
20．（9分）如图，AB是⊙O的直径，且AB＝6，点M为⊙O外一点，且MA，MC分别切⊙O于点A、C．点D是两条线段BC与AM延长线的交点．
（1）求证：DM＝AM；
（2）直接回答：
①当CM为何值时，四边形AOCM是正方形？
②当CM为何值时，△CDM为等边三角形？

21．（10分）如图，抛物线（b、c为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为．
（1）求该抛物线的函数关系式与C点坐标；
（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？

22．（10分）若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数y＝的图象与性质．列表：
x
…
﹣3
﹣
﹣2
﹣
﹣1
﹣
0

1

2

3
…
y
…


1

2

1

0

1

2
…
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．

（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点A（﹣5，y1），B（﹣，y2），C（x1，），D（x2，6）在函数图象上，则y1　 　y2，x1　 　x2；（填“＞”，“＝”或“＜”）
②当函数值y＝2时，求自变量x的值；
③在直线x＝﹣1的右侧的函数图象上有两个不同的点P（x3，y3），Q（x4，y4），且y3＝y4，求x3+x4的值；
④若直线y＝a与函数图象有三个不同的交点，求a的取值范围．
23．（11分）（1）【问题发现】
如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　 　
（2）【拓展研究】
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】
当正方形CDEF旋转到B，E，F三点共线的时候，直接写出线段AF的长．


2021年河南省南阳市镇平县中考数学模拟试卷（一）
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．（3分）下列四个数：﹣2，1，﹣，π，其中最小的数是（　　）
A．﹣2 B．1 C．﹣ D．π
【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．
【解答】解：根据实数比较大小的方法，可得
﹣2＜﹣＜1＜π，
∴四个数：﹣2，1，﹣，π，其中最小的数是﹣2．
故选：A．
2．（3分）舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约499.5亿千克，这个数用科学记数法应表示为（　　）
A．4.995×1011 B．49.95×1010
C．0.4995×1011 D．4.995×1010
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥1时，n是非负数；当原数的绝对值＜1时，n是负数．
【解答】解：将499.5亿用科学记数法表示为：4.995×1010．
故选：D．
3．（3分）六个大小一样的正方体搭成的几何体如图所示，则关于它的视图说法正确的是（　　）

A．正视图的面积最大 B．俯视图的面积最大
C．左视图的面积最大 D．三个视图的面积一样大
【分析】观察图形，分别表示出三视图由几个正方形组成，再比较其面积的大小．
【解答】解：观察图形可知，几何体的正视图由4个正方形组成，俯视图由5个正方形组成，左视图由4个正方形组成，所以俯视图的面积最大．
故选：B．
4．（3分）下列调查方式，你认为最合适的是（　　）
A．了解北京市每天的流动人口数，采用抽样调查方式
B．旅客上飞机前的安检，采用抽样调查方式
C．了解北京市居民“一带一路”期间的出行方式，采用全面调查方式
D．日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式
【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
【解答】解：A、了解北京市每天的流动人口数，采用抽样调查方式，正确；
B、旅客上飞机前的安检，采用全面调查方式，故错误；
C、了解北京市居民“一带一路”期间的出行方式，抽样调查方式，故错误；
D、日光灯管厂要检测一批灯管的使用寿命，采用抽样调查方式，故错误；
故选：A．
5．（3分）如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（　　）

A．30° B．40° C．50° D．60°
【分析】先根据三角形外角的性质求出∠BEF的度数，再根据平行线的性质得到∠2的度数．
【解答】解：如图，∵∠BEF是△AEF的外角，∠1＝20°，∠F＝30°，
∴∠BEF＝∠1+∠F＝50°，
∵AB∥CD，
∴∠2＝∠BEF＝50°，
故选：C．

6．（3分）下列一元二次方程中，没有实数根的是（　　）
A．x2﹣2x＝0 B．2x2﹣4x+3＝0 C．x2+4x﹣1＝0 D．3x2＝5x﹣2
【分析】分别计算出四个方程的根的判别式的值，判断各方程的根的情况即可．
【解答】解：A、因为Δ＝（﹣2）2﹣4×1×0＝4＞0，则方程有两个不相等的实数根，所以A选项不符合题意；
B、因为Δ＝（﹣4）2﹣4×2×3＝﹣8＜0，则方程没有实数解，所以B选项符合题意；
C、因为Δ＝42﹣4×1×（﹣1）＝20＞0，则方程有两个不相等的实数根，所以C选项不符合题意；
D、原方程即为3x2﹣5x+2＝0，因为Δ＝（﹣5）2﹣4×3×2＝1＞0，则方程有两个不相等的实数根，所以D选项不符合题意．
故选：B．
7．（3分）在四边形ABCD中，∠B＝90°，AC＝4，AB∥CD，DH垂直平分AC，点H为垂足．设AB＝x，AD＝y，则y关于x的函数关系用图象大致可以表示为（　　）

A． B．
C． D．
【分析】由△DAH∽△CAB，得＝，求出y与x关系，再确定x的取值范围即可解决问题．
【解答】解：∵DH垂直平分AC，
∴DA＝DC，AH＝HC＝2，
∴∠DAC＝∠DCH，
∵CD∥AB，
∴∠DCA＝∠BAC，
∴∠DAH＝∠BAC，∵∠DHA＝∠B＝90°，
∴△DAH∽△CAB，
∴＝，
∴＝，
∴y＝，
∵AB＜AC，
∴x＜4，
∴图象是D．
故选：D．

8．（3分）如图，已知∠AOB．按照以下步骤作图：
①以点O为圆心，以适当的长为半径作弧，分别交∠AOB的两边于C，D两点，连接CD．
②分别以点C，D为圆心，以大于线段OC的长为半径作弧，两弧在∠AOB内交于点E，连接CE，DE．
③连接OE交CD于点M．
下列结论中错误的是（　　）

A．∠CEO＝∠DEO B．CM＝MD
C．∠OCD＝∠ECD D．S四边形OCED＝CD•OE
【分析】利用基本作图得出角平分线的作图，进而解答即可．
【解答】解：由作图步骤可得：OE是∠AOB的角平分线，
∴∠CEO＝∠DEO，CM＝MD，S四边形OCED＝CD•OE，
但不能得出∠OCD＝∠ECD，
故选：C．
9．（3分）如图，半圆O的直径AB＝2，AP是半圆O的切线，C是射线AP上一动点（不与点A重合），连接BC，交半圆O于点M，若MN垂直且平分OA，则图中阴影部分的面积为（　　）

A． B． C． D．
【分析】连接OM，过点O作OH⊥BM于H，根据直角三角形的性质求出∠OMN＝30°，根据扇形面积公式、三角形的公式计算，得到答案．
【解答】解：连接OM，过点O作OH⊥BM于H，
∵MN垂直且平分OA，
∴ON＝OA＝OM＝，
∴∠OMN＝30°，
∴∠MON＝60°，
∴∠MOB＝120°，
∵OM＝OB，OH⊥BM，
∴∠MOH＝60°，∠OBH＝30°，
∴OH＝OM＝，MH＝OM＝，
∴BM＝，
∵AP是半圆O的切线，
∴∠CAB＝90°，
∴AC＝AB•tan∠ABC＝2×＝，
∴S阴影部分＝××2﹣﹣××+（﹣××）＝，
故选：A．

10．（3分）如图，在平面直角坐标系xOy中，A（4，0），B（0，3），C（4，3），I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I′的坐标为（　　）

A．（﹣2，3） B．（﹣3，2） C．（3，﹣2） D．（2，﹣3）
【分析】直接利用直角三角形的性质得出其内切圆半径，进而得出I点坐标，再利用旋转的性质得出对应点坐标．
【解答】解：过点作IF⊥AC于点F，IE⊥OA于点E，
∵A（4，0），B（0，3），C（4，3），
∴BC＝4，AC＝3，
则AB＝5，
∵I是△ABC的内心，
∴I到△ABC各边距离相等，等于其内切圆的半径，
∴IF＝1，故I到BC的距离也为1，
则AE＝1，
故IE＝3﹣1＝2，
OE＝4﹣1＝3，
则I（3，2），
∵△ABC绕原点逆时针旋转90°，
∴I的对应点I'的坐标为：（﹣2，3）．
故选：A．

二.填空题（每小题3分，共15分）
11．（3分）设a＝﹣1，a在两个相邻整数之间，则这两个整数是　3，4　．
【分析】根据二次根式的性质得出＜＜，推出4＜＜5，都减去1即可得出答案．
【解答】解：∵4＜＜5，
∴4﹣1＜﹣1＜5﹣1，
∴3＜﹣1＜4，
故答案为：3，4．
12．（3分）已知x＝3满足关于a的不等式，则这个不等式的解是 　a＜4　．
【分析】把x＝3代入不等式得到关于a的不等式，解不等式求出a的范围，
【解答】解：把x＝3代入关于a的不等式得：9﹣＞2，
解得：a＜4，
∴不等式的解集为a＜4，
故答案为a＜4．
13．（3分）三张背面完全相同的数字牌，它们的正面分别印有数字1，2，3，将它们背面朝上，洗匀后随机抽取一张，记录牌上的数字并把牌放回，再重复这样的步骤，得到数字a，b，则a≥b的概率是 　　．
【分析】画树状图得出所有等可能结果，再从中找到符合条件的结果数，继而利用概率公式可得答案．
【解答】解：根据题意画图如下：

由树状图知，共有9种等可能结果，其中a≥b的有6种，
则则a≥b的概率是 ＝；
故答案为：．
14．（3分）如图1，△ABC为直角三角形，∠C＝90°，四边形DEFG为矩形，且点C、B、E、F在同一条直线上，点B与点E重合，AC＝DE．Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移，当点C与点F重合时停止．设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2，运动时间xs．反映ycm2与xs之间函数关系的大致图象如图2，则矩形DEFG的面积为 　12　cm2．

【分析】分析△ABC的运动，可知分三种情况，当点C与点E重合前，点C与点E重合后点B与点F重合前，点B与点F重合后点C与点F重合前．由此可得BC＝2，BF＝6，再由2＜x＜6时，重合面积即△ABC的面积，可得AC的长，即DE的长，最后即可求解．
【解答】解：结合图1的运动和图2可知，
当点C和点E重合时，x＝2，当点B和点F重合时，x＝4，
∴EF＝6，BC＝2，
当2＜x＜6时，y＝AC•BC＝2，
∴AC＝2，
∴DE＝AC＝2，
∴矩形DEFG的面积为：2×6＝12（cm2）．
故答案为：12．
15．（3分）如图，已知Rt△ABC中，∠B＝90°，∠A＝60°，AC＝2+4，点M、N分别在线段AC、AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为　或　．

【分析】依据△DCM为直角三角形，需要分两种情况进行讨论：当∠CDM＝90°时，△CDM是直角三角形；当∠CMD＝90°时，△CDM是直角三角形，分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质，即可得到折痕MN的长．
【解答】解：分两种情况：
①如图，当∠CDM＝90°时，△CDM是直角三角形，

∵在Rt△ABC中，∠B＝90°，∠A＝60°，AC＝2+4，
∴∠C＝30°，AB＝AC＝，
由折叠可得，∠MDN＝∠A＝60°，
∴∠BDN＝30°，
∴BN＝DN＝AN，
∴BN＝AB＝，
∴AN＝2BN＝，
∵∠DNB＝60°，
∴∠ANM＝∠DNM＝60°，
∴∠AMN＝60°，
∴AN＝MN＝；
②如图，当∠CMD＝90°时，△CDM是直角三角形，

由题可得，∠CDM＝60°，∠A＝∠MDN＝60°，
∴∠BDN＝60°，∠BND＝30°，
∴BD＝DN＝AN，BN＝BD，
又∵AB＝，
∴AN＝2，BN＝，
过N作NH⊥AM于H，则∠ANH＝30°，
∴AH＝AN＝1，HN＝，
由折叠可得，∠AMN＝∠DMN＝45°，
∴△MNH是等腰直角三角形，
∴HM＝HN＝，
∴MN＝，
故答案为：或．
三.解答题（共2小题，满分17分）
16．（8分）先化简，再求值：（+a﹣3）÷，其中a为不等式组的整数解．
【分析】先化简分式，然后将a的整数解代入求值．
【解答】解：原式＝•
＝
＝，
解不等式组得：＜a＜3，
∴不等式组的整数解为a＝2，
当a＝2时，
原式＝＝．
17．（9分）今年春节，新型冠状病毒感染的肺炎疫情牵动着全国人民的心，为了提高意识，共克时艰，共渡难关，綦江区某校开展了“全民行动•共同抗疫”的自我防护知识网上答题竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100），下面给出了部分信息：
七年级10名学生的竞赛成绩是：90，80，90，86，99，96，96，100，89，82
八年级10名学生的竞赛成绩在C组中的数据是：94，90，94
七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
90
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：
（1）直接写出上述图表中a，b，c的值．
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）．
（3）该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？

【分析】（1）求出C组所占的百分比，再根据频率之和为1，即可求出a的值，依据中位数、众数的计算方法可求出八年级的中位数，和七年级的众数，确定b、c的值；
（2）通过比较平均数、中位数、众数得出答案；
（3）样本估计总体，样本中“优秀”占，因此根据总体720人的是“优秀”人数．
【解答】解：（1）3÷10＝30%，1﹣30%﹣10%﹣20%＝40%，因此a＝40，
A组有2人，B组有1人，C组有3人，D组有4人，
将他们的成绩从小到大排列后，处在中间位置的两个数都是94，因此中位数是94，即b＝94，
七年级竞赛成绩出现次数最多的是90和96，都出现2次，因此众数是90和96，即c＝90和96，
答：a＝40，b＝94，c＝90和96；
（2）八年级学生掌握防溺水安全知识较好，虽然七、八年级竞赛成绩的平均数相同，但是八年级的竞赛成绩的中位数、众数都比七年级的高，因此八年级学生掌握防溺水安全知识较好；
（3）720×＝468（人）．
答：估计参加竞赛活动成绩优秀（x≥90）的学生人数是468人．

18．（9分）如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G在同一直线上，cos80°≈0.018，sin80°≈0.98，≈1.414），此时小强头部E点与地面DK的距离是多少？

【分析】过点F作FN⊥DK于N，过点E作EM⊥FN于M．求出MF、FN的长，即可解决问题．
【解答】解：过点F作FN⊥DK于N，过点E作EM⊥FN于M，如图所示：
∵EF+FG＝166cm，FG＝100cm，
∴EF＝166﹣100＝66（cm），
∵∠FGK＝80°，
∴FN＝100•sin80°≈100×0.98＝98（cm），
∵∠EFG＝125°，
∴∠EFM＝180°﹣125°﹣10°＝45°，
∴FM＝66•cos45°＝66×＝33≈46.66（cm），
∴MN＝FN+FM≈144.66（cm），
即此时小强头部E点与地面DK相距约为144.66cm；

19．（9分）商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为p＝，且其日销售量y（kg）与时间t（天）的关系如表：
时间t（天）
1
3
6
10
20
40
…
日销售量y（kg）
118
114
108
100
80
40
…
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
【分析】（1）设y＝kt+b，利用待定系数法即可解决问题．
（2）日利润＝日销售量×每公斤利润，据此分别表示前24天和后24天的日利润，根据函数性质求最大值后比较得结论．
【解答】解：（1）设y＝kt+b，把t＝1，y＝118；t＝3，y＝114代入得到：

解得，
∴y＝﹣2t+120．
将t＝30代入上式，得：y＝﹣2×30+120＝60．
所以在第30天的日销售量是60kg．

（2）设利润为W元
当1≤t≤24时，W＝（p﹣20）y＝﹣t2+10t+1200＝﹣（t﹣10）2+1250，
当t＝10时，W最大＝1250元
当25≤t≤48时，W＝（p﹣20）y＝t2﹣116t+3360＝（t﹣58）2﹣4，
当t＝25时，W最大＝1085元
∵1250＞1085，
∴综上，当t＝10时，W最大＝1250元．
20．（9分）如图，AB是⊙O的直径，且AB＝6，点M为⊙O外一点，且MA，MC分别切⊙O于点A、C．点D是两条线段BC与AM延长线的交点．
（1）求证：DM＝AM；
（2）直接回答：
①当CM为何值时，四边形AOCM是正方形？
②当CM为何值时，△CDM为等边三角形？

【分析】（1）根据切线的性质得：MA⊥OA，MC⊥OC，MC＝MA，根据等边对等角得：∠OCB＝∠B，由等角的余角相等可得结论；
（2）①直接可得CM＝OA＝3；
②先根据等边三角形定义可得：DM＝CM，∠D＝60°，由切线长定理得CM＝AM＝DM，可得结论．
【解答】解：（1）如图1，连接OM，

∵MA，MC分别切⊙O于点A、C，
∴MA⊥OA，MC⊥OC，MC＝MA
∴∠OAM＝∠OCM＝90°，
∵OC＝OB，
∴∠OCB＝∠B，
又∵∠DCM+∠OCB＝90°，∠D+∠B＝90°，
∴∠DCM＝∠D，
∴DM＝MC，
∴DM＝MA；
（2）①当CM＝OA＝3时，如图2，四边形AOCM是正方形；

②连接OM，如图3，∵△DCM是等边三角形，
∴CM＝DM，∠D＝60°，
∵∠DAB＝90°，
∴∠B＝30°，
∴∠AOC＝2∠B＝60°，
∵AB＝6，
∴tan∠B＝tan30°＝＝，
∴AD＝2，
同理得CM＝AM，
∴AM＝CM＝DM，
∴CM＝AD＝．

21．（10分）如图，抛物线（b、c为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为．
（1）求该抛物线的函数关系式与C点坐标；
（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？

【分析】（1）根据已知条件得到B（0，），A（﹣6，0），解方程组得到抛物线的函数关系式为：y＝﹣x2﹣x+，于是得到C（1，0）；
（2）由点M（m，0），过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，得到D（m，m+），当DE为底时，作BG⊥DE于G，根据等腰三角形的性质得到EG＝GD＝ED，GM＝OB＝，列方程即可得到结论．
【解答】解：（1）在y＝x+中，令x＝0，则y＝，令y＝0，则x＝﹣6，
∴B（0，），A（﹣6，0），
把B（0，），A（﹣6，0）代入y＝﹣x2+bx+c得，
，
∴，
∴抛物线的函数关系式为：y＝﹣x2﹣x+，
令y＝0，则0＝﹣x2﹣x+，
∴x1＝﹣6，x2＝1，
∴C（1，0）；
（2）∵点M（m，0），过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，
∴D（m，m+），当DE为底时，
如图1，作BG⊥DE于G，则EG＝GD＝ED，GM＝OB＝，
∵DM+DG＝GM＝OB，
∴m++（﹣m2﹣m+﹣m﹣）＝，
解得：m1＝﹣4，m2＝0（不合题意，舍去），
∴当m＝﹣4时，△BDE恰好是以DE为底边的等腰三角形．

22．（10分）若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数y＝的图象与性质．列表：
x
…
﹣3
﹣
﹣2
﹣
﹣1
﹣
0

1

2

3
…
y
…


1

2

1

0

1

2
…
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．

（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点A（﹣5，y1），B（﹣，y2），C（x1，），D（x2，6）在函数图象上，则y1　＜　y2，x1　＜　x2；（填“＞”，“＝”或“＜”）
②当函数值y＝2时，求自变量x的值；
③在直线x＝﹣1的右侧的函数图象上有两个不同的点P（x3，y3），Q（x4，y4），且y3＝y4，求x3+x4的值；
④若直线y＝a与函数图象有三个不同的交点，求a的取值范围．
【分析】（1）描点连线即可；
（2）①A与B在y＝﹣上，y随x的增大而增大，所以y1＜y2；C与D在y＝|x﹣1|上，观察图象可得x1＜x2；
②当y＝2时，2＝|x﹣1|，则有x＝3或x＝﹣1；
③由图可知﹣1≤x≤3时，点关于x＝1对称，当y3＝y4时x3+x4＝2；
④由图象可知，0＜a＜2；
【解答】解：（1）如图所示：
（2）①A（﹣5，y1），B（﹣，y2），
A与B在y＝﹣上，y随x的增大而增大，∴y1＜y2；
C（x1，），D（x2，6），
C与D在y＝|x﹣1|上，观察图象可得x1＜x2；
故答案为＜，＜；
②当y＝2时，x≤﹣1时，有2＝﹣，∴x＝﹣1；
当y＝2时，x＞﹣1时，有2＝|x﹣1|，∴x＝3或x＝﹣1（舍去），
故x＝﹣1或x＝3；
③∵P（x3，y3），Q（x4，y4）在x＝﹣1的右侧，
∴﹣1≤x≤3时，点P，Q关于x＝1对称，
则有y3＝y4，
∴x3+x4＝2；
④由图象可知，0＜a＜2；

23．（11分）（1）【问题发现】
如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　BE＝AF　
（2）【拓展研究】
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】
当正方形CDEF旋转到B，E，F三点共线的时候，直接写出线段AF的长．

【分析】（1）先利用等腰直角三角形的性质得出AD＝，再得出BE＝AB＝2，即可得出结论；
（2）先利用三角函数得出，同理得出，夹角相等即可得出△ACF∽△BCE，进而得出结论；
（3）分两种情况计算，当点E在线段BF上时，如图2，先利用勾股定理求出EF＝CF＝AD＝，BF＝，即可得出BE＝﹣，借助（2）得出的结论，当点E在线段BF的延长线上，同前一种情况一样即可得出结论．
【解答】解：（1）在Rt△ABC中，AB＝AC＝2，
根据勾股定理得，BC＝AB＝2，
点D为BC的中点，
∴AD＝BC＝，
∵四边形CDEF是正方形，
∴AF＝EF＝AD＝，
∵BE＝AB＝2，
∴BE＝AF，
故答案为BE＝AF；
（2）无变化；
如图2，在Rt△ABC中，AB＝AC＝2，
∴∠ABC＝∠ACB＝45°，
∴sin∠ABC＝＝，
在正方形CDEF中，∠FEC＝∠FED＝45°，
在Rt△CEF中，sin∠FEC＝，
∴，
∵∠FCE＝∠ACB＝45°，
∴∠FCE﹣∠ACE＝∠ACB﹣∠ACE，
∴∠FCA＝∠ECB，
∴△ACF∽△BCE，
∴，
∴BE＝AF，
∴线段BE与AF的数量关系无变化；
（3）当点E在线段BF上时，如图2，
由（1）知，CF＝EF＝CD＝，
在Rt△BCF中，CF＝，BC＝2，
根据勾股定理得，BF＝，
∴BE＝BF﹣EF＝﹣，
由（2）知，BE＝AF，
∴AF＝﹣1，
当点E在线段BF的延长线上时，如图3，
由（1）知，CF＝EF＝CD＝，
在Rt△BCF中，CF＝，BC＝2，
根据勾股定理得，BF＝，
∴BE＝BF+EF＝+，
由（2）知，BE＝AF，
∴AF＝+1．
即：当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为﹣1或+1．