2021年江苏省镇江市中考数学一模试卷 解析版

这是一份2021年江苏省镇江市中考数学一模试卷 解析版，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021年江苏省镇江市中考数学一模试卷
一、选择题（本大题共有8小题，每小题0分，共24分.在每小题所给出的四个选项中，恰有一项符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．|﹣5|的值是（　　）
A．5 B．﹣5 C． D．
2．下面计算正确的是（　　）
A．3a+2b＝5ab B．5a2b﹣2ba2＝3a2b
C．﹣（6x+2y）＝﹣6x+2y D．（﹣2a）2＝﹣4a2
3．如图所示，该几何体的俯视图是（　　）

A． B． C． D．
4．如图，在⊙O中，∠ACB＝67°，点P在劣弧上，∠AOP＝42°，则∠BOP的度数为（　　）

A．25° B．90° C．92° D．109°
5．将二次函数y＝﹣x2+2x+3（0≤x≤4）位于x轴下方的图象沿x轴向上翻折，与原二次函数位于x轴上方的部分组成一个新图象，这个新图象对应的函数最大值与最小值之差为（　　）
A．1 B．3 C．4 D．5
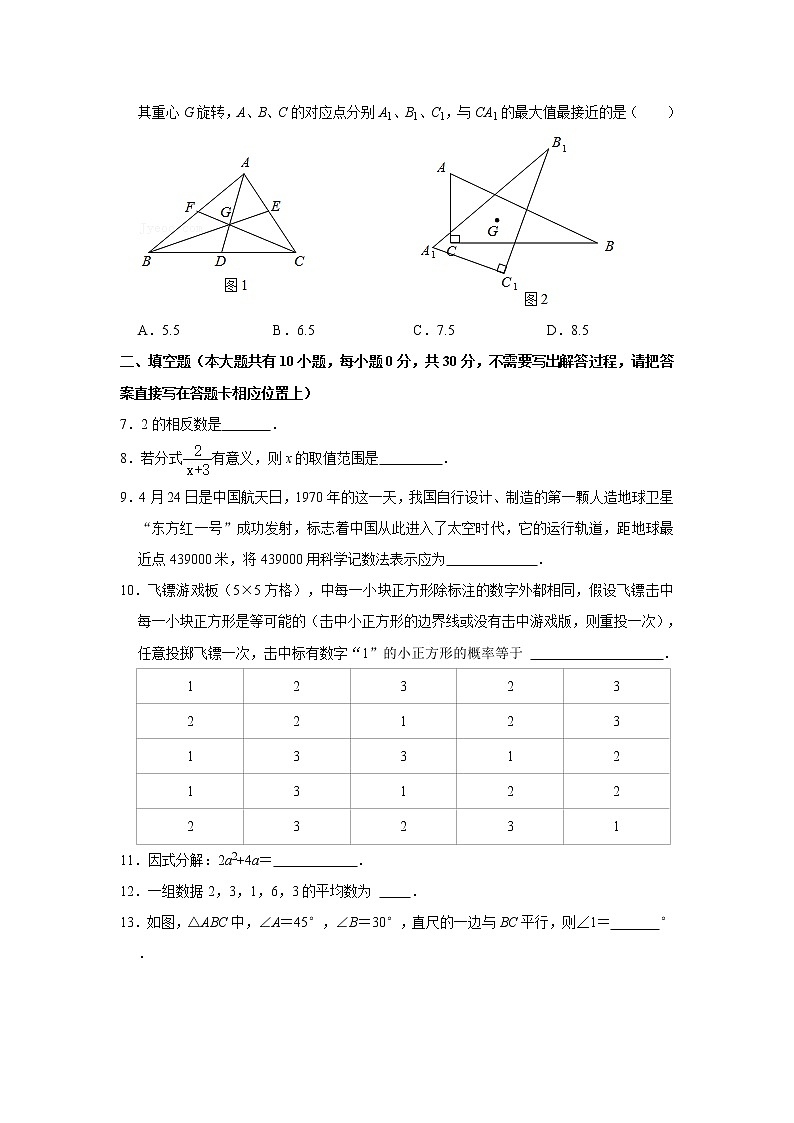
6．我们知道，△ABC的重心就是三条中线AD、BE、CF的交点G，如图1，其中，如图2，Rt△ABC中，∠C＝90°，AC＝4，BC＝8，将Rt△ABC绕其重心G旋转，A、B、C的对应点分别A1、B1、C1，与CA1的最大值最接近的是（　　）

A．5.5 B．6.5 C．7.5 D．8.5
二、填空题（本大题共有10小题，每小题0分，共30分，不需要写出解答过程，请把答案直接写在答题卡相应位置上）
7．2的相反数是　 　．
8．若分式有意义，则x的取值范围是　 　．
9．4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439000米，将439000用科学记数法表示应为　 　．
10．飞镖游戏板（5×5方格），中每一小块正方形除标注的数字外都相同，假设飞镖击中每一小块正方形是等可能的（击中小正方形的边界线或没有击中游戏版，则重投一次），任意投掷飞镖一次，击中标有数字“1”的小正方形的概率等于 　 　．
1
2
3
2
3
2
2
1
2
3
1
3
3
1
2
1
3
1
2
2
2
3
2
3
1
11．因式分解：2a2+4a＝　 　．
12．一组数据2，3，1，6，3的平均数为 　 　．
13．如图，△ABC中，∠A＝45°，∠B＝30°，直尺的一边与BC平行，则∠1＝　 　°．

14．已知一次函数y＝x+2，当﹣3≤x≤3时，y的最小值等于 　 　．
15．已知一元二次方程x2+2x﹣m＝0有两个不相等的实数根，则m的取值范围是 　 　．
16．如图，等腰△ABC中，AB＝AC，CD平分∠ACB，若S△ACD：S△BCD＝3：2，则cos∠ACB＝　 　．

17．公元前240年前后，在希腊的亚历山大城图书馆当馆长的埃拉托色尼（Eratosthenes）通过测得有关数据，求得了地球圆周的长度．他是如何测量的呢？如图所示，由于太阳距离地球很远，太阳射来的光线可以看作平行线，在同时刻，光线与A城和地心的连线OP所夹的锐角记为∠1，光线与B城和地心的连线OQ重合，通过测量A，B两城间的距离（即AB）和∠1的度数，利用圆的有关知识，地球圆周的长度就可以大致算出来了．已知AB≈768km，若∠1≈7.2°，则地球的周长约为 　 　km．

18．在平面直角坐标系中，已知点A（1，﹣2），点B（2，1），点P在一次函数y＝x+b的图象上，若满足PAB＝45°的点P只有1个，则b的取值范围是 　 　．
三、解答题（本大题共有10小题，共86分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（1）计算：．
（2）化简：．
20．（1）解方程：；
（2）解不等式组：．
21．D是△ABC的边AB上的一点，E是边BC边的中点，过点C作AB的平行线，交DE的延长线于点F，连接CD、BF．
（1）求证：DE＝EF．
（2）已知BC＝8，DF＝6，当DB＝　 　时，四边形CDBF是菱形．

22．随着信息技术的迅猛发展，移动支付已成为一种常见的支付方式．在一次购物中，马老师和赵老师都随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付．求两位老师恰好一人用“微信”支付，一人用“银行卡”支付的概率．
23．如图1，点C在线段AB上，图中共有3条线段AB、AC和BC，若其中有一条线段的长度是另一条线段长度的两倍，则称点C是线段AB的“二倍点”；如图2，一次函数y＝ax+2a（a＞0）与x轴交于点A，与y轴交于点B，与反比例函数y＝的图象位于第一象限的部分相交于点C．
（1）求点A的坐标；
（2）若点B是线段AC的“二倍点”，则a＝　 　．

24．为增强同学们的科学防疫意识，学校开展了以“科学防疫，健康快乐”为主题的安全知识竞赛，从全校学生中随机抽取了男、女各40名，并将数据进行整理分析，得到如下信息．
信息一：女生成绩扇形统计图和男生成绩频数分布直方图如图；
（数据分组为A组：x＜70，B组：70≤x＜80，C组：80≤x＜90，D组：90≤x≤100）

信息二：女生C组中全部15名学生的成绩为：
86，87，81，83，88，84，85，87，86，89，82，88，89，85，89；
信息三：男、女生两组数据的相关统计数据如表：（单位：分）

平均数
中位数
众数
满分率
女生
90
b
c
25%
男生
90
88
98
15%
（1）扇形统计图中A组学生有 　 　人，表格中的中位数b＝　 　，众数c＝　 　．
（2）若成绩在90分（包含90分）以上为优秀，请估计该校1600名学生此次知识竞赛中优秀的人数．
25．如图，公园里有一棵大树（AB）与一棵小树（CD），受测量工具、地理环境及安全等因素影响不能直接测量它们的高度之差，小明与小丽手中有一副含30°角的直角三角尺和一根皮尺，小明首先在与树根B、D成一条直线的点E处用三角尺测得小树CD顶部C的仰角为30°，然后他向后移动调整，在M处用三角尺测得大树AB顶部A的仰角也是30°，点M仍然与B、D在一条直线上，然后他俩用皮尺测得BD＝4.5米，EM＝1.5米，求两棵树的高度之差．

26．阅读材料：
《见微知著》谈到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂，从部分到整体，由低维到高维，知识与方法上的类比是探索发展的重要途径，是思想阀门发现新问题、新结论的重要方法．
例如：已知xy＝1，求+的值．
解：原式＝．
问题解决：
（1）已知xy＝1．
①代数式的值为 　 　．
②求证．
（2）若x满足（2021﹣x）2+（2020﹣x）2＝4043，求（2021﹣x）（2020﹣x）．
27．如图1，△ABC中，AB＝5，AC＝3，BC＝7，半径为r的⊙O经过点A且与BC相切，切点M在线段BC上（包含点M与点B、C重合的情况）．
（1）半径r的最小值等于 　 　；
（2）设BM＝x，求半径r关于x的函数表达式；
（3）当BM＝1时，请在图2中作点M及满足条件的⊙O．（要求：尺规作图，不写作法，保留作图痕迹，并用2B铅笔或黑色水笔加黑加粗）

28．如图1，二次函数y＝（x﹣2）2的图象记为C1，与y轴交于点A，其顶点为B，二次函数y＝（x﹣h）2﹣h+1（h＞2）的图象记为C2，其顶点为D，图象C1、C2相交于点P，设点P的横坐标为m．
（1）求证：点D在直线AB上．
（2）求m和h的数量关系；
（3）平行于x轴的直线l1经过点P与图象C交于另一点E，与图象C2交于另一点F，若＝2，求h的值．
（4）如图2，过点P作平行于AB的直线l2，与图象C2交于另一点Q，连接DQ，当DQ⊥AB时，h＝　 　（直接写出结果）．


2021年江苏省镇江市中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共有8小题，每小题0分，共24分.在每小题所给出的四个选项中，恰有一项符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．|﹣5|的值是（　　）
A．5 B．﹣5 C． D．
【分析】绝对值的性质：正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0．
【解答】解：根据负数的绝对值等于它的相反数，得：|﹣5|＝5．故选A．
2．下面计算正确的是（　　）
A．3a+2b＝5ab B．5a2b﹣2ba2＝3a2b
C．﹣（6x+2y）＝﹣6x+2y D．（﹣2a）2＝﹣4a2
【分析】根据合并同类项、去括号及积的乘方法则即可得到答案．
【解答】解：3a与2b不是同类项，故A不符合题意；
5a2b﹣2ba2＝3a2b，故B符合题意；
﹣（6x+2y）＝﹣6x﹣2y，故C不符合题意；
（﹣2a）2＝4a2，故D不符合题意；
故选：B．
3．如图所示，该几何体的俯视图是（　　）

A． B． C． D．
【分析】根据从上面看得到的图形是俯视图，可得答案．
【解答】解：从上面看，是一行两个矩形．
故选：B．
4．如图，在⊙O中，∠ACB＝67°，点P在劣弧上，∠AOP＝42°，则∠BOP的度数为（　　）

A．25° B．90° C．92° D．109°
【分析】根据圆周角定理得出∠AOB＝2∠ACB，求出∠AOB的度数，再求出答案即可．
【解答】解：∵∠ACB＝67°，
∴∠AOB＝2∠ACB＝134°，
∵∠AOP＝42°，
∴∠BOP＝∠AOB﹣∠AOP＝134°﹣42°＝92°，
故选：C．
5．将二次函数y＝﹣x2+2x+3（0≤x≤4）位于x轴下方的图象沿x轴向上翻折，与原二次函数位于x轴上方的部分组成一个新图象，这个新图象对应的函数最大值与最小值之差为（　　）
A．1 B．3 C．4 D．5
【分析】令 y＝0，则 x1＝﹣1，x2＝3，令x＝0，则y＝3，再求出抛物线于x轴右侧的交点A（3，0），翻折后的函数表达式为：﹣y′＝﹣x2+2x+3，当 x＝4 时，y′＝5，当 0≤x≤4 时，函数的最小值为0，最大值为5，即可求出函数最大值与最小值之差．
【解答】解：如下图，函数y＝﹣x2+2x+3的对称轴为x＝1，故顶点P的坐标为（1，4），

令 y＝0，则 x1＝﹣1，x2＝3，
令x＝0，则y＝3，
设抛物线于x 轴右侧的交点A（3，0），
根据点的对称性，图象翻折后图象关于x 轴对称，故翻折后的函数表达式为：﹣y′＝﹣x2+2x+3，当 x＝4 时，y′＝5，
∴当 0≤x≤4 时，函数的最小值为 0，最大值为5，
故函数最大值与最小值之差为5，
故选：D．
6．我们知道，△ABC的重心就是三条中线AD、BE、CF的交点G，如图1，其中，如图2，Rt△ABC中，∠C＝90°，AC＝4，BC＝8，将Rt△ABC绕其重心G旋转，A、B、C的对应点分别A1、B1、C1，与CA1的最大值最接近的是（　　）

A．5.5 B．6.5 C．7.5 D．8.5
【分析】连接AG并延长交BC于点E，然后利用重心的性质和已知条件求出AG的长度和CG的长度．再以点G为圆心，OG为半径作圆，连接CG并延长交⊙G与点F，此时CF的长度即为CA1的最大值．
【解答】解：连接AG并延长交BC于点E，
∵点G为△ABC的重心，BC＝8，
∴CE＝4，AG：AE＝2：3，
∴AE＝＝4，
∴AG＝＝＝，
以点G为圆心，OG为半径作圆，连接CG并延长交⊙G与点F，交AB于点H，此时CF的长即为CA1的最大值，
∵AC＝4，BC＝8，
∴AB＝4，
∵点G是△ABC的重心，∠ACB＝90°，
∴CH＝AB＝2，
∴CG＝CH＝×2＝，
∴CF＝CG+GF＝CG+GA＝+≈6.75，
故选：B．

二、填空题（本大题共有10小题，每小题0分，共30分，不需要写出解答过程，请把答案直接写在答题卡相应位置上）
7．2的相反数是　﹣2　．
【分析】根据相反数的定义可知．
【解答】解：2的相反数是﹣2．
故答案为：﹣2
8．若分式有意义，则x的取值范围是　x≠﹣3　．
【分析】根据分式分母不等于零列出不等式，解不等式即可．
【解答】解：由题意得，x+3≠0，
解得，x≠﹣3，
故答案为：x≠﹣3．
9．4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439000米，将439000用科学记数法表示应为　4.39×105　．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【解答】解：439000用科学记数法表示为：4.39×105．
故答案为：4.39×105．
10．飞镖游戏板（5×5方格），中每一小块正方形除标注的数字外都相同，假设飞镖击中每一小块正方形是等可能的（击中小正方形的边界线或没有击中游戏版，则重投一次），任意投掷飞镖一次，击中标有数字“1”的小正方形的概率等于 　　．
1
2
3
2
3
2
2
1
2
3
1
3
3
1
2
1
3
1
2
2
2
3
2
3
1
【分析】用标有数字“1”的小正方形的个数除以小正方形的总个数可得．
【解答】解：标有数字“1”的小正方形的概率等于，
故答案为：．
11．因式分解：2a2+4a＝　2a（a+2）　．
【分析】观察发现，系数的最大公约数是2，相同字母的最低次幂是a．故公因式是2a．
【解答】解：原式＝2a（a+2）．
12．一组数据2，3，1，6，3的平均数为 　3　．
【分析】根据算术平均数的定义求解即可．
【解答】解：数据2，3，1，6，3的平均数为＝3，
故答案为：3．
13．如图，△ABC中，∠A＝45°，∠B＝30°，直尺的一边与BC平行，则∠1＝　75　°．

【分析】如图，根据三角形外角的性质，得∠1＝∠A+∠AME．欲求∠1，需求∠AME．根据平行线的性质，由DE∥BC，得∠B＝∠AME＝30°，从而解决此题．
【解答】解：如图．

由题意得：DE∥BC．
∴∠B＝∠AME＝30°．
∴∠1＝∠A+∠AME＝45°+30°＝75°．
故答案为：75．
14．已知一次函数y＝x+2，当﹣3≤x≤3时，y的最小值等于 　﹣3　．
【分析】由k＝＞0，利用一次函数的性质可得出y随x的增大而增大，结合﹣3≤x≤3，即可得出当x＝﹣3时y取得最小值，再利用一次函数图象上点的坐标特征即可求出y的最小值．
【解答】解：∵k＝＞0，
∴y随x的增大而增大．
又∵﹣3≤x≤3，
∴当x＝﹣3时，y取得最小值，此时y＝×（﹣3）+2＝﹣3．
故答案为：﹣3．
15．已知一元二次方程x2+2x﹣m＝0有两个不相等的实数根，则m的取值范围是 　m＞﹣1　．
【分析】根据判别式的意义得到Δ＝22﹣4×（﹣m）＞0，然后解不等式即可．
【解答】解：根据题意得Δ＝22﹣4×1×（﹣m）＞0，
解得m＞﹣1．
故答案为：m＞﹣1．
16．如图，等腰△ABC中，AB＝AC，CD平分∠ACB，若S△ACD：S△BCD＝3：2，则cos∠ACB＝　　．

【分析】如图，过点A作AD⊥BC于点D，DN⊥AC于N，DM⊥BC于M．欲求cos∠ACB，需求CD：AC．根据角平分线的性质，由CD平分∠ACB，DM⊥BC于M，DN⊥AC于点N，得DM＝DN．由，，得S△ACD：S△BCD＝AC：BC＝3：2．根据等腰三角形的性质，由AB＝AC，AD⊥BC，得BD＝CD＝，那么CD：AC＝1：3，从而解决此题．
【解答】解：如图，过点A作AE⊥BC于点E，DN⊥AC于N，DM⊥BC于M．

∵CD平分∠ACB，DM⊥BC于M，DN⊥AC于点N，
∴DM＝DN．
∵，，
∴S△ACD：S△BCD＝AC：BC＝3：2．
∵AB＝AC，AE⊥BC，
∴BE＝CE＝．
∴CE：AC＝1：3．
∴COS∠ACB＝．
故答案为：．
17．公元前240年前后，在希腊的亚历山大城图书馆当馆长的埃拉托色尼（Eratosthenes）通过测得有关数据，求得了地球圆周的长度．他是如何测量的呢？如图所示，由于太阳距离地球很远，太阳射来的光线可以看作平行线，在同时刻，光线与A城和地心的连线OP所夹的锐角记为∠1，光线与B城和地心的连线OQ重合，通过测量A，B两城间的距离（即AB）和∠1的度数，利用圆的有关知识，地球圆周的长度就可以大致算出来了．已知AB≈768km，若∠1≈7.2°，则地球的周长约为 　38400　km．

【分析】首先根据弧长公式求出地球的半径，再利用圆的周长公式即可求解．
【解答】解：∵太阳射来的光线可以看作平行线，
∴∠AOB＝∠1≈7.2°．
设地球的半径为R千米，由题意得
＝768，
解得R＝，
∴地球的周长约为2π×＝38400（千米）．
故答案为：38400．
18．在平面直角坐标系中，已知点A（1，﹣2），点B（2，1），点P在一次函数y＝x+b的图象上，若满足PAB＝45°的点P只有1个，则b的取值范围是 　b＞﹣　．
【分析】连接AB，过点A作AC∥OB，证明△AOB是等腰直角三角形，然后结合一次函数图象的平移，利用y＝x+b由y＝x 平移得到b的取值范围．
【解答】解：如图：连接AB，过点A作AC∥OB，

∵A（1，﹣2），点B（2，1），
∴AB＝，
AO＝，
BO＝，
∴AO2+BO2＝AB2，AO＝BO，
∴△AOB是等腰直角三角形，
∴∠OBA＝∠OAB＝45°，
又∵OB∥AC，
∴∠OBA＝∠BAC＝45°，
∴满足PAB＝45°的点P在射线AC或射线AO上，
设直线OB的解析式为y＝kx，
把B（2，1）代入，得：2k＝1，
解得：k＝，
∴直线OB的解析式为y＝x，
所以直线AC的解析式为y＝x+m，
把A（1，﹣2）代入y＝x+m中，
+m＝﹣2，
解得：m＝﹣，
又∵满足PAB＝45°的点P只有1个，且点P在一次函数y＝x+b上，
∴点P在射线AO上，且不与点A重合，
∴b＞﹣，
故答案为：b＞﹣．
三、解答题（本大题共有10小题，共86分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（1）计算：．
（2）化简：．
【分析】（1）根据负整数指数幂、特殊角的三角函数值、算术平方根可以解答本题；
（2）先对括号内的分式通分，然后作差，再计算括号外面的式子，将除法转化为乘法，然后约分即可．
【解答】解：（1）
＝2+1﹣3
＝0；
（2）
＝•
＝（x+1）﹣（x﹣1）
＝x+1﹣x+1
＝2．
20．（1）解方程：；
（2）解不等式组：．
【分析】（1）方程两边都乘x﹣2得出x+x﹣2＝8，求出x，再进行检验即可；
（2）先求出每个不等式的解集，再求出不等式组的解集即可．
【解答】解：（1）方程两边都乘x﹣2，得x+x﹣2＝8，
解得：x＝5，
检验：当x＝5时，x﹣2≠0，所以x＝5是原方程的解，
即原方程的解是x＝5；

（2），
解不等式①，得x≤﹣2，
解不等式②，得x＞﹣4，
所以不等式组的解集是﹣4＜x≤﹣2．
21．D是△ABC的边AB上的一点，E是边BC边的中点，过点C作AB的平行线，交DE的延长线于点F，连接CD、BF．
（1）求证：DE＝EF．
（2）已知BC＝8，DF＝6，当DB＝　5　时，四边形CDBF是菱形．

【分析】（1）欲证明四边形CDBF是平行四边形只要证明CF∥DB，CF＝DB即可；
（2）根据平行四边形的性质得到DE＝DF＝3，BE＝BC＝4，根据勾股定理的逆定理得到BC⊥DF，由菱形的判定定理即可得到结论．
【解答】（1）证明：∵CF∥AB，
∴∠ECF＝∠EBD．
∵E是BC中点，
∴CE＝BE．
∵∠CEF＝∠BED，
∴△CEF≌△BED（ASA）．
∴CF＝BD．
∴四边形CDBF是平行四边形，
∴DE＝EF；
（2）解：当DB＝5时，四边形CDBF是菱形，
理由：∵四边形CDBF是平行四边形，
∴DE＝DF＝3，BE＝BC＝4，
∵DE2+BE2＝32+42＝52＝BD2，
∴∠BED＝90°，
∴BC⊥DF，
∴四边形CDBF是菱形，
故答案为：5．
22．随着信息技术的迅猛发展，移动支付已成为一种常见的支付方式．在一次购物中，马老师和赵老师都随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付．求两位老师恰好一人用“微信”支付，一人用“银行卡”支付的概率．
【分析】将“微信”记为A、“支付宝”记为B、“银行卡”记为C，列表可得所有结果数，共有9种等可能的结果，其中一人选择“微信”支付，一人选择“银行卡”支付的结果有2种，利用概率公式求解可得．
【解答】解：将“微信”记为A、“支付宝”记为B、“银行卡”记为C，
列表法如下：

A
B
C
A
（A，A）
（B，A）
（C，A）
B
（A，B）
（B，B）
（C，B）
C
（A，C）
（B，C）
（C，C）
∴共有9种等可能的结果，其中一人选择“微信”支付，一人选择“银行卡”支付的结果有2种，
∴两位老师恰好一人选择“微信”支付，一人选择“银行卡”支付的概率为．
23．如图1，点C在线段AB上，图中共有3条线段AB、AC和BC，若其中有一条线段的长度是另一条线段长度的两倍，则称点C是线段AB的“二倍点”；如图2，一次函数y＝ax+2a（a＞0）与x轴交于点A，与y轴交于点B，与反比例函数y＝的图象位于第一象限的部分相交于点C．
（1）求点A的坐标；
（2）若点B是线段AC的“二倍点”，则a＝　　．

【分析】（1）把y＝0代入y＝ax+2a即可求得x＝﹣2，即可得到A（﹣2，0）；
（2）根据题意AB＝2BC，由OA＝2，即可求得C的横坐标为1，代入反比例函数解析式求得C的坐标，把C的坐标代入y＝ax+2a，即可求得a的值．
【解答】解：（1）令y＝0，则ax+2a＝0，
∴x＝﹣2，
∴A（﹣2，0）；
（2）∵y＝ax+2a（a＞0）与x轴交于点A，与y轴交于点B，
∴B（0，2a），
∵点B是线段AC的“二倍点”，
∴AB＝2BC，
∴C的横坐标为1，
把x＝1代入y＝，得y＝4，
∴C（1，4），
代入y＝ax+2a得，4＝a+2a，
解得a＝，
故答案为：．
24．为增强同学们的科学防疫意识，学校开展了以“科学防疫，健康快乐”为主题的安全知识竞赛，从全校学生中随机抽取了男、女各40名，并将数据进行整理分析，得到如下信息．
信息一：女生成绩扇形统计图和男生成绩频数分布直方图如图；
（数据分组为A组：x＜70，B组：70≤x＜80，C组：80≤x＜90，D组：90≤x≤100）

信息二：女生C组中全部15名学生的成绩为：
86，87，81，83，88，84，85，87，86，89，82，88，89，85，89；
信息三：男、女生两组数据的相关统计数据如表：（单位：分）

平均数
中位数
众数
满分率
女生
90
b
c
25%
男生
90
88
98
15%
（1）扇形统计图中A组学生有 　1　人，表格中的中位数b＝　88　，众数c＝　100　．
（2）若成绩在90分（包含90分）以上为优秀，请估计该校1600名学生此次知识竞赛中优秀的人数．
【分析】（1）根据扇形统计图中，各个部分所占的百分比，可求出B组、D组人数，再由C组人数为15人，进而求出A组人数，然后再根据中位数、众数的意义求出中位数和众数即可确定b、c的值；
（2）求出样本中，优秀所占的百分比即可估计总体中优秀所占的百分比，进而求出相应的人数．
【解答】解：（1）抽样调查中40名女生的成绩在“B组”的有40×20%＝8（人），
在“D组”的有40×40%＝16（人），
因为“C组”的有15人，
所以：“A组”的有40﹣8﹣16﹣15＝1（人），
将这40名女生成绩从小到大排列，处在中间位置的两个数都是88分，因此中位数是88分，即b＝88，
这40名女生成绩出现次数最多的是满分100，共出现40×25%＝10人次，因此众数是100，即c＝100，
故答案为：1，88，100；
（2）1600×＝580（人），
答：该校1600名学生此次知识竞赛中优秀的人数为580人．
25．如图，公园里有一棵大树（AB）与一棵小树（CD），受测量工具、地理环境及安全等因素影响不能直接测量它们的高度之差，小明与小丽手中有一副含30°角的直角三角尺和一根皮尺，小明首先在与树根B、D成一条直线的点E处用三角尺测得小树CD顶部C的仰角为30°，然后他向后移动调整，在M处用三角尺测得大树AB顶部A的仰角也是30°，点M仍然与B、D在一条直线上，然后他俩用皮尺测得BD＝4.5米，EM＝1.5米，求两棵树的高度之差．

【分析】延长NF交AB于点G，交CD于点H，可得四边形BGHD，四边形DHFE，四边形FNME是矩形，根据锐角三角函数表示AG＝（6+HF），CH＝HF，进而可得AB﹣CD＝（AG+BG）﹣（CH+DH）＝AG﹣CH＝（6+HF）﹣HF，可求大树AB比小树CD高多少米．
【解答】解：如图，延长NF交AB于点G，交CD于点H，

根据题意可知：
四边形BGHD，四边形DHFE，四边形FNME是矩形，
∴GH＝BD＝4.5米，HF＝DE，FN＝EM＝1.5米，
在Rt△ANG中，∠AGN＝90°，∠ANG＝30°，
∴AG＝GN•tan∠ANG
＝（GH+HF+FN）•tan30°
＝（4.5+HF+1.5）
＝（6+HF）（米），
在Rt△CFH中，∠CHF＝90°，∠CFH＝30°，
∴CH＝HF•tan∠CFH
＝HF•tan30°
＝HF，
∴AB﹣CD＝（AG+BG）﹣（CH+DH）
＝AG﹣CH
＝（6+HF）﹣HF
＝2 （米）．
答：大树AB比小树CD高2米．
26．阅读材料：
《见微知著》谈到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂，从部分到整体，由低维到高维，知识与方法上的类比是探索发展的重要途径，是思想阀门发现新问题、新结论的重要方法．
例如：已知xy＝1，求+的值．
解：原式＝．
问题解决：
（1）已知xy＝1．
①代数式的值为 　1　．
②求证．
（2）若x满足（2021﹣x）2+（2020﹣x）2＝4043，求（2021﹣x）（2020﹣x）．
【分析】（1）①由题意可得xy＝1，代入所求式中可求值；
②由题意可得xy＝1，则x2021y2021＝1，代入第1个加数中可求值；
（2）把2021﹣x看作a，把2020﹣x看作b，根据完全平方公式可得答案．
【解答】（1）①解：∵xy＝1，
∴+＝＝+＝+＝+＝1，
故答案为：1；
②证明：∵xy＝1，
∴x2021y2021＝1，
∴+
＝+
＝+
＝1；
（2）∵[（2021﹣x）﹣（2020﹣x）]2
＝（2021﹣x）2﹣2（2021﹣x）（2020﹣x）+（2020﹣x）2，
∵（2021﹣x）2+（2020﹣x）2＝4043，
∴4043﹣2（2021﹣x）（2020﹣x）＝1，
∴（2021﹣x）（2020﹣x）＝2021．
27．如图1，△ABC中，AB＝5，AC＝3，BC＝7，半径为r的⊙O经过点A且与BC相切，切点M在线段BC上（包含点M与点B、C重合的情况）．
（1）半径r的最小值等于 　　；
（2）设BM＝x，求半径r关于x的函数表达式；
（3）当BM＝1时，请在图2中作点M及满足条件的⊙O．（要求：尺规作图，不写作法，保留作图痕迹，并用2B铅笔或黑色水笔加黑加粗）

【分析】（1）当AM⊥BC交BC于点M时，此时半径r最小，设BM＝x，利用勾股定理列出方程52﹣x2＝（3）2﹣（7﹣x）2，即可解题；
（2）连接OM，过点A作AD⊥BC交BC于点D，过点O作OF⊥AD交AD于点F，在Rt△AOF中，由勾股定理得：即r2＝（4﹣x）2+（3﹣r）2，整理成一般式即可；
（3）过点M作BC的垂线MF，连接AM，作AM的垂直平分线HD，HD和MF的交点即是⊙O的位置，再以O为圆心，OM为半径作圆即可．
【解答】解：（1）当AM⊥BC交BC于点M时，此时半径r最小，
设BM＝x，如图所示，

在Rt△ABM和Rt△ACM中，由勾股定理得：
∴52﹣x2＝（3）2﹣（7﹣x）2，
解得：x＝4，
∴AM＝＝3，
∴半径r＝，
故答案为：；
（2）如图所示，连接OM，过点A作AD⊥BC交BC于点D，过点O作OF⊥AD交AD于点F，

由（1）知，AD＝3，BM＝x，BD＝4，OA＝r，
∴OF＝MD＝4﹣x，AF＝AD﹣DF＝3﹣r，
在Rt△AOF中，由勾股定理得：
即r2＝（4﹣x）2+（3﹣r）2，
整理得：r＝，
∵点M在线段BC上，
∴0≤x≤7，
∴r＝（0≤x≤7）；
（3）如图所示，过点M作BC的垂线MF，连接AM，
作AM的垂直平分线HD，HD和MF的交点即是⊙O的位置，
再以O为圆心，OM为半径作圆即可．

28．如图1，二次函数y＝（x﹣2）2的图象记为C1，与y轴交于点A，其顶点为B，二次函数y＝（x﹣h）2﹣h+1（h＞2）的图象记为C2，其顶点为D，图象C1、C2相交于点P，设点P的横坐标为m．
（1）求证：点D在直线AB上．
（2）求m和h的数量关系；
（3）平行于x轴的直线l1经过点P与图象C交于另一点E，与图象C2交于另一点F，若＝2，求h的值．
（4）如图2，过点P作平行于AB的直线l2，与图象C2交于另一点Q，连接DQ，当DQ⊥AB时，h＝　4或20　（直接写出结果）．

【分析】（1）先求出A、B的坐标，再代入一次函数解析式，最后验证即可；
（2）联立一次函数的二次函数的解析式求出x与h的关系，再根据图象交于点P即可得出结论；
（3）求出点P、E、F的橫坐标，即可得出结果；
（4）得出四边形BPQD为矩形，再分两种情况讨论求解即可．
【解答】（1）证明：对y＝（x﹣2）2，
当x＝0时，y＝1，即A（0，1），
当y＝0时，（x﹣2）2＝0，解得x＝2，即B（2，0），
设直线AB的解析式为y＝kx+b，则
，解得：，
∴直线AB的解析式为y＝﹣x+1，
∴当x＝h时，y＝﹣h+1，
∵y＝（x﹣h）2﹣h+1（h＞2）的顶点D的坐标为（h，﹣h+1），
∴点D在直线AB上．
（2）解：联立，得x＝h，
∵图象C1、C2相交于点P，点P的横坐标为m，
∴m＝h．
（3）∵直线l1∥x轴，交抛物线y＝（x﹣2）2于点E和点P，交抛物线y＝（x﹣h）2﹣h+1（h＞2）于点F，点P的横坐标为h，
∴点E的横坐标为4﹣h，点F的横坐标为h，
∴PF＝h﹣h＝h，PE＝h﹣（4﹣h）＝h﹣4，
∵＝2，
∴＝2，
解得：h＝8．
（4）由题意得，图象C1平移得到图象C2，
∴BD＝PQ，BD∥PQ，
∴当DQ⊥AB时，四边形BPQD为矩形，
∴∠ABP＝90°，
作PM⊥x轴于点M，则∠BMP＝∠AOB＝90°，∠ABO+∠PBM＝90°，
∵∠ABO+∠BAO＝90°，
∴∠BAO＝∠PBM＝90°，
∴△AOB∽△BMP，
∴，
∵A（0，1），B（2，0），
∴AO＝1，BO＝2，
∴，
由（2）得点P的坐标为（h，），
∴BM＝h﹣2，PM＝，
∴，
解得：h＝20或h＝4，
故答案为：4或20．