人教版新课标A必修33.3.1几何概型课堂教学课件ppt

这是一份人教版新课标A必修33.3.1几何概型课堂教学课件ppt，共27页。PPT课件主要包含了新课导入，传授新知，几何概型的定义，对比看看，生活模型，几何模型，课堂练习，方法小结，几何概型的特点，课堂小结等内容，欢迎下载使用。

【想一想】估计图形中阴影部分中芝麻数
2. 向左图边长为2正方形中随机地撒100粒芝麻，假设每一粒芝麻落在正方形内的每个位置的可能性都相同，如果区域B中的芝麻数20， 那么在区域B的面积大约多少？
【想一想】估计图形中阴影部分面积
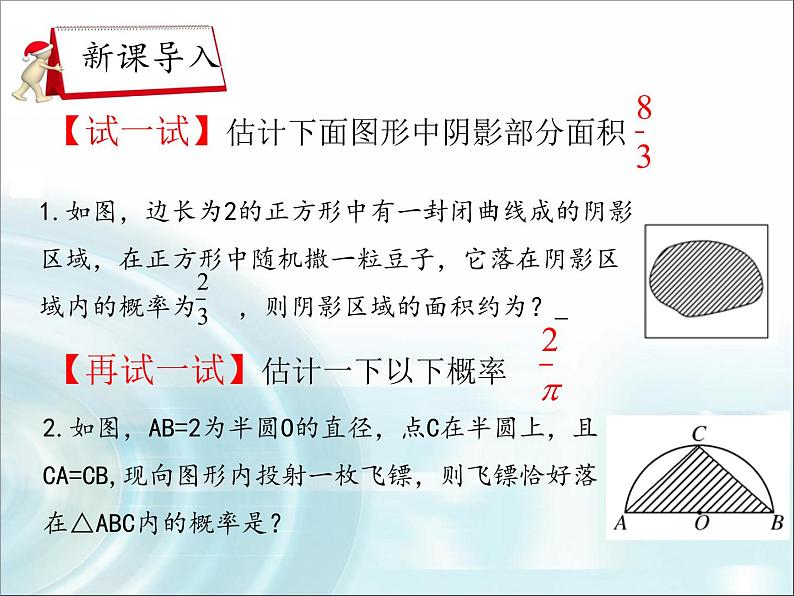
【试一试】估计下面图形中阴影部分面积
向平面上有限区域G内随机的投掷一枚飞镖，若飞镖落在子区域M的概率与M的面积成正比，而与G的形状、位置无关，即则称这样的概率模型为几何概率模型，简称几何概型。
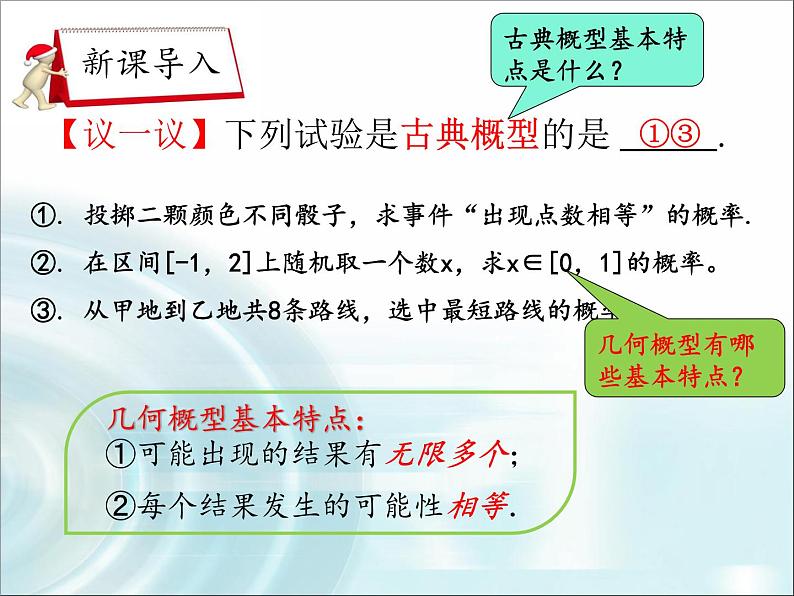
【议一议】下列试验是古典概型的是 .
①. 投掷二颗颜色不同骰子，求事件“出现点数相等”的概率.②. 在区间[-1，2]上随机取一个数x，求x∈[0，1]的概率。③. 从甲地到乙地共8条路线，选中最短路线的概率.
古典概型基本特点是什么？
几何概型有哪些基本特点？
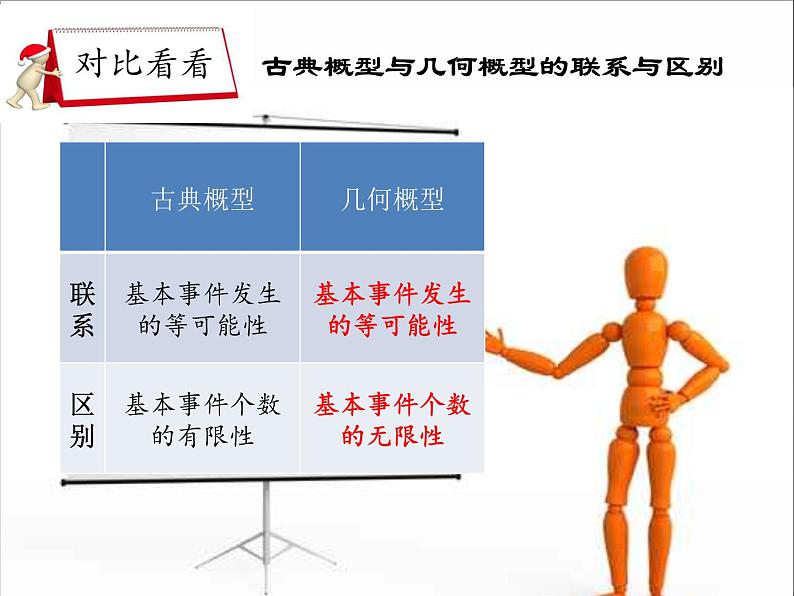
古典概型与几何概型的联系与区别
举例说明生活中常见的几何概型-----交通灯问题
一个路口的交通灯，红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为40秒。当你到达路口时，看见下列三种情况的概率各是多少？（1）红灯；（2）黄灯；（3）不是红灯。
简单几何概型概率的求法
模型1：与长度有关的几何概型问题
例1：取一根长度为30cm的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不小于10cm的概率有多大？
解：记“剪得两段绳长都不小于10cm”为事件A. 把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生.由于中间一段的长度等于绳长的1/3.
模型2：与面积有关的几何概型问题
例1：取一个边长为2a的正方形及其内切圆(如图),随机地向正方形内丢一粒豆子,求豆子落入圆内的概率.
解:记“豆子落入圆内”为事件A,则
例2：一海豚在水中自由游弋，水池长30m，宽20m的长方形，求此刻海豚嘴尖离岸边不超过2m的概率.
例3：我校早上7：40开始上课，假设我校学生小张与小王在早上7：10～7：30之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早5分钟到校的概率为________．
例1：有一杯1升的水，其中含有1个H7N9个细菌，用一个小杯从这杯水中取出0.1升，求小杯水中含有这个细菌的概率.
模型3：与体积有关的几何概型问题
例2：一只小蜜蜂在一个棱长为3的正方体内自由飞行，若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1，则称其为“安全飞行”,求蜜蜂“安全飞行”的概率.
1.在区间[0，10]上任意取一个整数x，则x不大于3的概率是。
2.在区间[0，10]上任意取一个实数x，则x不大于3的概率为。
3.假设车站每隔10分钟发一班车，随机到达车站，问 等车时间不超过3分钟的概率为______.
4.如图，矩形ABCD中，点E为边CD上任意一点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率为__.
用几何概型解决实际问题的方法.
(1)选择适当的观察角度，转化为几何概型.
(2)把随机事件A转化为与之对应区域的 长度（面积、体积）
(3)利用几何概率公式计算
2.古典概型与几何概型的区别：
3.几何概型的概率公式：
4.几何概型问题的概率的求解:
1.P153 A组 1、2题
“抛阶砖”是国外游乐场的典型游戏之一，阶砖平面是由若干个边长为a的小正方形阶砖组成.参与者只须将半径为 r（２r＜a） 的“金币”，抛向离身边若干距离的阶砖平面上，抛出的“金币”若恰好落在任何一个阶砖之内（不与阶砖的边相碰），便可获奖，求参加者获奖的概率.