江苏省南通市海门区2021-2022学年第一学期期中质量调研模拟卷 九年级数学（word版含答案）

南通市海门区2021-2022学年度第一学期期中质量调研模拟卷

九年级数学

一、 选择（每小题3分，共30分）

1.下面四个手机应用图标中是中心对称图形的是（   ）           

A.                     B.                     C.                     D. 

2.关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根0，则a值为（　　）

A.1     B.﹣1   C.±1   D.0

3.已知点A（a，﹣1）与B（2，b）是关于原点O的对称点，则（　　）

A．a＝﹣2，b＝﹣1   B．a＝﹣2，b＝1   C．a＝2，b＝﹣1  D．a＝2，b＝1

4.已知圆锥的底面周长为，高为4cm，则它的侧面展开图的圆心角是　　

A．     B．     C．     D．

5.一个暗箱里装有10个黑球，6个白球，14个红球，搅匀后随机摸出一个球，则摸到白球的概率是

A、     B、     C、       D、

6.如图，内接于，连接OA，OB，若，则的度数是　  　

A．     B．     C．     D．

7.市工会组织篮球比赛庆五一，赛制为单循环形式(每两队之间都赛一场)，共进行了36场比赛，则这次参加比赛的球队个数为(   )

A.11个           B.10个            C.8个          D.9个

8.如图，将△ABC绕点A逆时针旋转100°，得到△ADE，若点D在线段BC的延长线上，则∠B的大小为（　　）

A．60° B．50° C．45° D．40°

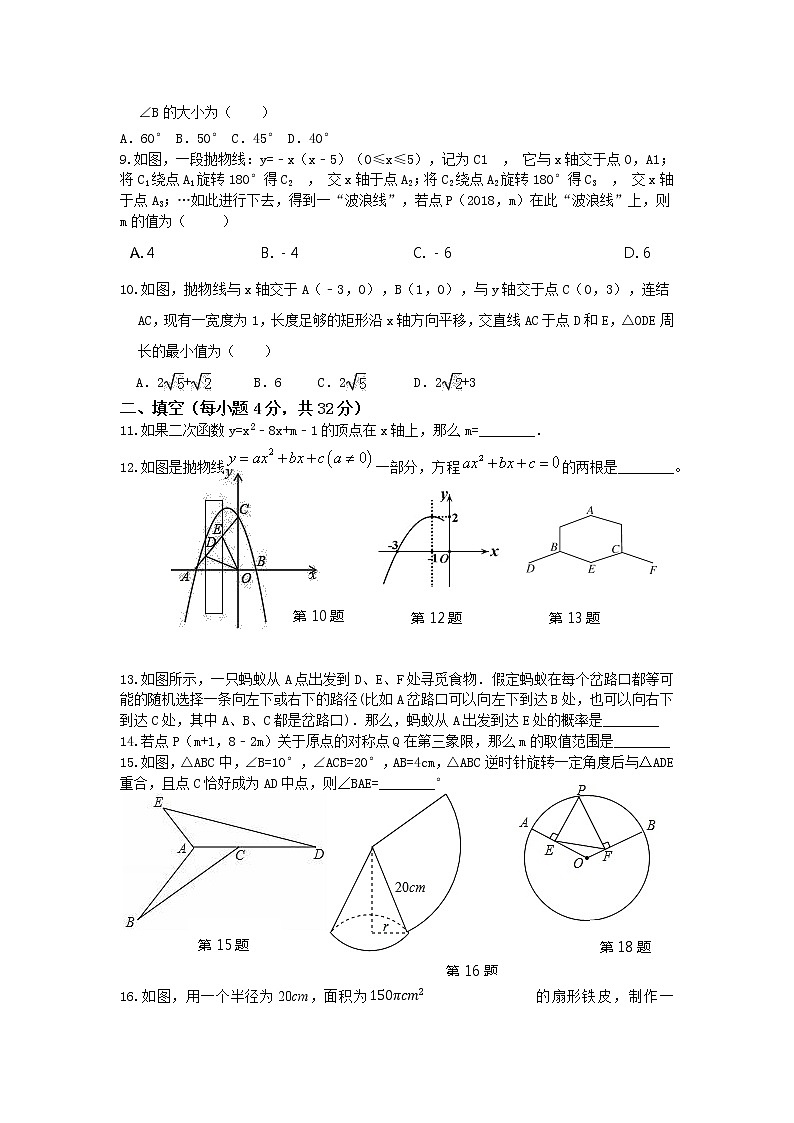
9.如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1  ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2  ， 交x轴于点A2；将C2绕点A2旋转180°得C3  ， 交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（   ）

A. 4                         B. ﹣4                           C. ﹣6                                         D. 6

10.如图，抛物线与x轴交于A（﹣3，0），B（1，0），与y轴交于点C（0，3），连结AC，现有一宽度为1，长度足够的矩形沿x轴方向平移，交直线AC于点D和E，△ODE周长的最小值为（　　）

  A．2+ B．6 C．2 D．2+3 

二、填空（每小题4分，共32分）

11.如果二次函数y=x2﹣8x+m﹣1的顶点在x轴上，那么m=________．

12.如图是抛物线一部分，方程的两根是________。

13.如图所示，一只蚂蚁从A点出发到D、E、F处寻觅食物．假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A、B、C都是岔路口)．那么，蚂蚁从A出发到达E处的概率是________

14.若点P（m+1，8﹣2m）关于原点的对称点Q在第三象限，那么m的取值范围是________

15.如图，△ABC中，∠B=10°，∠ACB=20°，AB=4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，则∠BAE=________°

16.如图，用一个半径为20cm，面积为的扇形铁皮，制作一个无底的圆锥不计接头损耗，则圆锥的底面半径r为______cm．

17.如果关于x的方程x2-ax+a2-3=0至少有一个正根，则实数a的取值范围是____________

18.如图，⊙O的半径为2，OA，OB是⊙O的半径，P是弧AB上任意一点，PE⊥OA于E，PF⊥OB于F，则EF的最大值为______．

三、解答

19.（10分）解方程

（1）                         

20. （10分）飞镖随机地掷在下面的靶子上（图中圆的半径平分半圆）
（1）飞镖投在区域A，B的概率各是多少？

（2）掷两次飞镖，都投在区域A中的概率是多少？列表或画树状图.

21. （10分）已知关于x的方程

求证：无论m取何值时，方程总有实数根；

若等腰三角形一边长为4，另两边恰好是此方程的根，求此三角形的另两边长．

22. （10分）如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．

（1）求∠ODC的度数；

（2）若OB=2，OC=3，求AO的长．

23. （12分）如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D，连接BE，过点O作OC∥BE交切线DE于点C，连接AC．
（1）求证：AC是 O的切线；  
（2）若BD=OB=4，求弦AE的长．

24. （12分）某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w=-2x+240，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求y与x的关系式；

（2）当x取何值时，y的值最大？

（3）如果公司想要在这段时间内获得2 250元的销售利润，销售单价应定为多少元？ 

25. （12分）如图，矩形OABC在平面直角坐标系中，点A在x轴正半轴，点C在y轴正半轴，OA=4，OC=3，抛物线经过O，A两点且顶点在BC边上，与直线AC交于点D．

（1）求抛物线的解析式； 

（2）求点D的坐标；

（3）若点M在抛物线上，点N在x轴上，以A，D，M，N为顶点的四边形是平行四边形，直接写出点N的坐标．

26. （12分）如图1，在△ABC中，∠ACB=90°，点P为△ABC内一点．

（1）连接PB，PC，将△BCP沿射线CA方向平移，得到△DAE，点B，C，P的对应点

分别为点D，A，E，连接CE．

①     依题意，请在图2中补全图形；

②     如果BP⊥CE，BP=3，AB=6，求CE的长．

（2）如图3，连接PA，PB，PC，求PA+PB+PC的最小值．

小慧的作法是：以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，那么就将PA+PB+PC的值转化为CP+PM+MN的值，连接CN，当点P落在CN上时，此题可解．

请你参考小慧的思路，在图3中证明PA+PB+PC=CP+PM+MN．

并直接写出当AC=BC=4时，PA+PB+PC的最小值．

南通市海门区2021-2022学年度第一学期期中质量调研模拟卷

九年级数学答题纸

一、        选择

二、填空

11. ________________________                     12. ________________________

13. ________________________                     14. ________________________

15. ________________________                     16. ________________________

17. ________________________                     18. ________________________

三、解答

19.

20.

21.

22.

23.

24.

25.

26.

南通市海门区2021-2022学年度第一学期期中质量调研模拟卷

九年级数学评分标准

11. 17     12. X1=1，x2=-3   13.    14. ﹣1＜m＜4  15. 60°16. 7.5

17. -≤a≤    18.  2

19.（1）x1=，x2=﹣3                               5’

 （2）x1=0，x2=3                                    5’

20.                                                 2’

                                                   4’

列表或画树状图                                       8’

 共16种可能，两次都投在区域A中有4种可能           9’

                                                   10’  

21.

证明：         

无论m取何值，这个方程总有实数根；                                        4’

若腰长为4，将代入原方程，得：

解得：                                                                

原方程为

解得：，

组成三角形的三边长度为2，4，4.                                           6’

若底边长为4，则此方程有两个相等实数根，

，即

此时方程为

解得：

由于，不能构成三角形，舍去；                             8’

所以三角形另外两边程度为4和2                                   10’

22.

解：（1）由旋转的性质得，CD=CO，∠ACD=∠BCO，         2’

∵∠ACB=60°，

∴∠DCO=60°，

∴△OCD为等边三角形，                                   4’

∴∠ODC=60°；                                            5’

（2）由旋转的性质得，AD=OB=2，

∵△OCD为等边三角形，

∴OD=OC=3，

∵∠BOC=150°，∠ODC=60°，

∴∠ADO=90°，                                             8’

在Rt△AOD中，由勾股定理得：AO==．          10’

23.

（1）证明：连接OE，
∵CD与圆O相切，
∴OE⊥CD，
∴∠CEO=90°，                                               2’
∵BE∥OC，
∴∠AOC=∠OBE，∠COE=∠OEB，
∵OB=OE，
∴∠OBE=∠OEB，
∴∠AOC=∠COE，
在△AOC和△EOC中，

∴△AOC≌△EOC（SAS），                                       4’
∴∠CAO=∠CEO=90°，
则AC与圆O相切；                                             6’
（2）在Rt△DEO中，BD=OB，
∴BE=OD=OB=4，                                               8’
∵OB=OE，
∴△BOE为等边三角形，
∴∠ABE=60°，                                                 10’
∵AB为圆O的直径，
∴∠AEB=90°，
∴AE= =．                                                  12’

24.

（1）y=（x-50）•w=（x-50）•（-2x+240）=-2x2+340x-12000，
因此y与x的关系式为：y=-2x2+340x-12000．                      4’
（2）y=-2x2+340x-12000=-2（x-85）2+2450，
∴当x=85时，在50＜x≤90内，y的值最大为2450．                8’
（3）当y=2250时，可得方程-2（x-85）2+2450=2250，
解这个方程，得x1=75，x2=95；                                   10’
根据题意，x2=95不合题意应舍去．
答：当销售单价为75元时，可获得销售利润2250元．                12’

25.

解：（1）设抛物线顶点为E，根据题意OA=4，OC=3，得：E（2，3），

设抛物线解析式为y=a（x﹣2）2+3，

将A（4，0）坐标代入得：0=4a+3，即a=﹣，

则抛物线解析式为y=﹣（x﹣2）2+3=﹣x2+3x；        4’

（2）设直线AC解析式为y=kx+b（k≠0），

将A（4，0）与C（0，3）代入得：

，

解得：，

故直线AC解析式为y=﹣x+3，                       6’

与抛物线解析式联立得：，

解得：或，

则点D坐标为（1，）；                              8’

（3）N1（2，0），                                   9’

N2（6，0），                                        10’

N3（﹣﹣1，0），                                  11’

N4（﹣1，0）．                                    12’

26. 解：（1）①如图1……………………… 2分

②如图2，连接BD、CD

∵△BCP沿射线CA方向平移，得到△DAE

∴BC∥AD且BC=AD

∵∠ACB=90°

∴四边形BCAD是矩形……………………… 4分

∴CD=AB=6

∵BP=3

∴DE= BP=3

∵BP⊥CE，BP∥DE

∴DE ⊥CE     ……………………… 6分

∴在Rt△DCE中，

CE=……………………… 8分

（2）证明：∵以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN.

∴△AMN≌△ABP，

∴MN=BP，PA=AM，∠PAM=60°

∴△PAM是等边三角形.

∴PA=PM

∴ PA+PB+PC=CP+PM+MN…………………… 10分

当AC=BC=4时，PA+PB+PC=．…… 12分