
人教版九年级上册数学--期中数学模拟测试卷2(附答案)
展开期中数学试卷1
一、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上。
1.(3分)下列电视台的台标,是中心对称图形的是( )
A. B.
C. D.
2.(3分)一元二次方程x2+4x=2配方后化为( )
A.(x+2)2=6 B.(x﹣2)2=6 C.(x+2)2=﹣6 D.(x+2)2=﹣2
3.(3分)ʘO的半径为5cm,点A到圆心O的距离OA=4cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
4.(3分)抛物线y=3x2先向下平移1个单位,再向左平移2个单位,所得的抛物线是( )
A.y=3(x+2)2﹣1 B.y=3(x﹣2)2+1
C.y=(x﹣2)2﹣1 D.y=3(x+2)2+1
5.(3分)如图所示,平行四边形ABCD的对角线交于点O,下列结论错误的是( )
A.平行四边形ABCD是中心对称图形
B.△AOB≌△COD
C.△AOB≌△BOC
D.△AOB与△BOC的面积相等
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
7.(3分)将一个底面半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )
A.54° B.126° C.136° D.144°
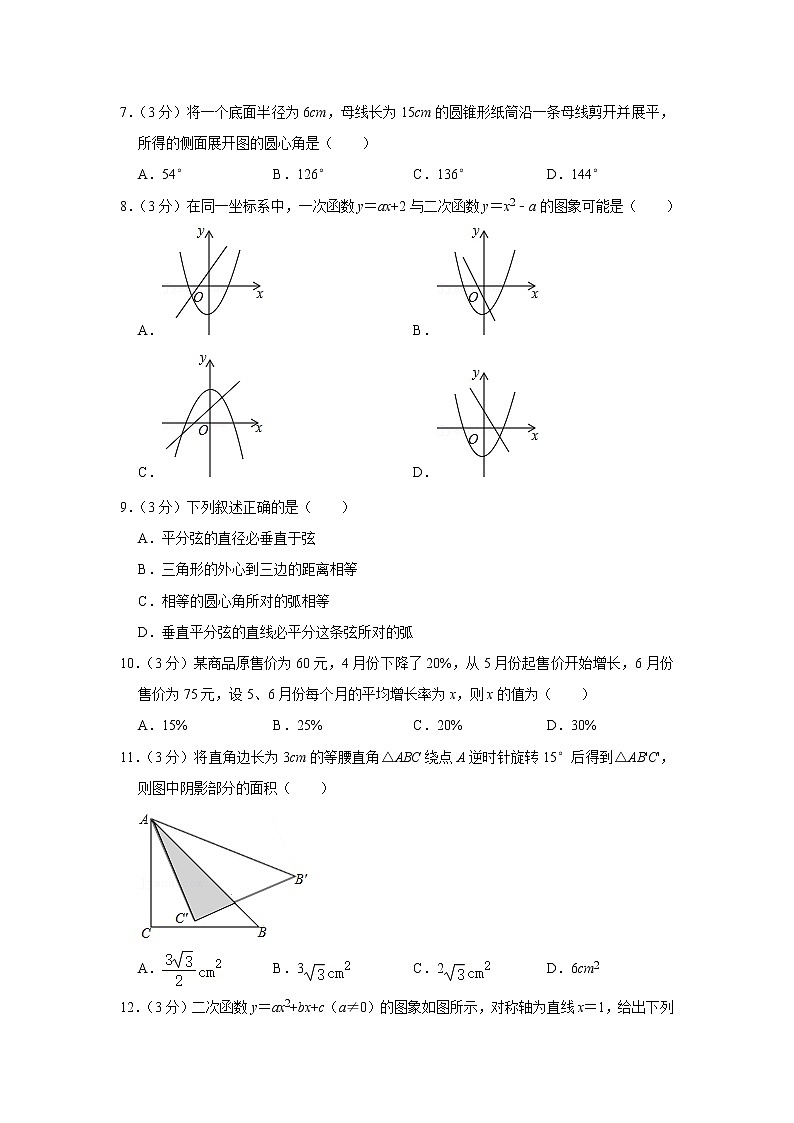
8.(3分)在同一坐标系中,一次函数y=ax+2与二次函数y=x2﹣a的图象可能是( )
A. B.
C. D.
9.(3分)下列叙述正确的是( )
A.平分弦的直径必垂直于弦
B.三角形的外心到三边的距离相等
C.相等的圆心角所对的弧相等
D.垂直平分弦的直线必平分这条弦所对的弧
10.(3分)某商品原售价为60元,4月份下降了20%,从5月份起售价开始增长,6月份售价为75元,设5、6月份每个月的平均增长率为x,则x的值为( )
A.15% B.25% C.20% D.30%
11.(3分)将直角边长为3cm的等腰直角△ABC绕点A逆时针旋转15°后得到△AB'C',则图中阴影部分的面积( )
A. B.3 C.2 D.6cm2
12.(3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,给出下列结论:①abc>0;②当x>2时,y>0;③8a+c>0;④3a+b<0,其中正确的结论有( )
A.①② B.①③ C.①③④ D.②④
二、填空题:本大题共6小题,每小题3分,共18分,把答案填写在答题卡的横线上。
13.(3分)与点P(2,﹣4)关于原点中心对称的点的坐标为 .
14.(3分)方程x2=x的解是 .
15.(3分)二次函数y=2(x+1)2﹣3的图象的对称轴是直线 .
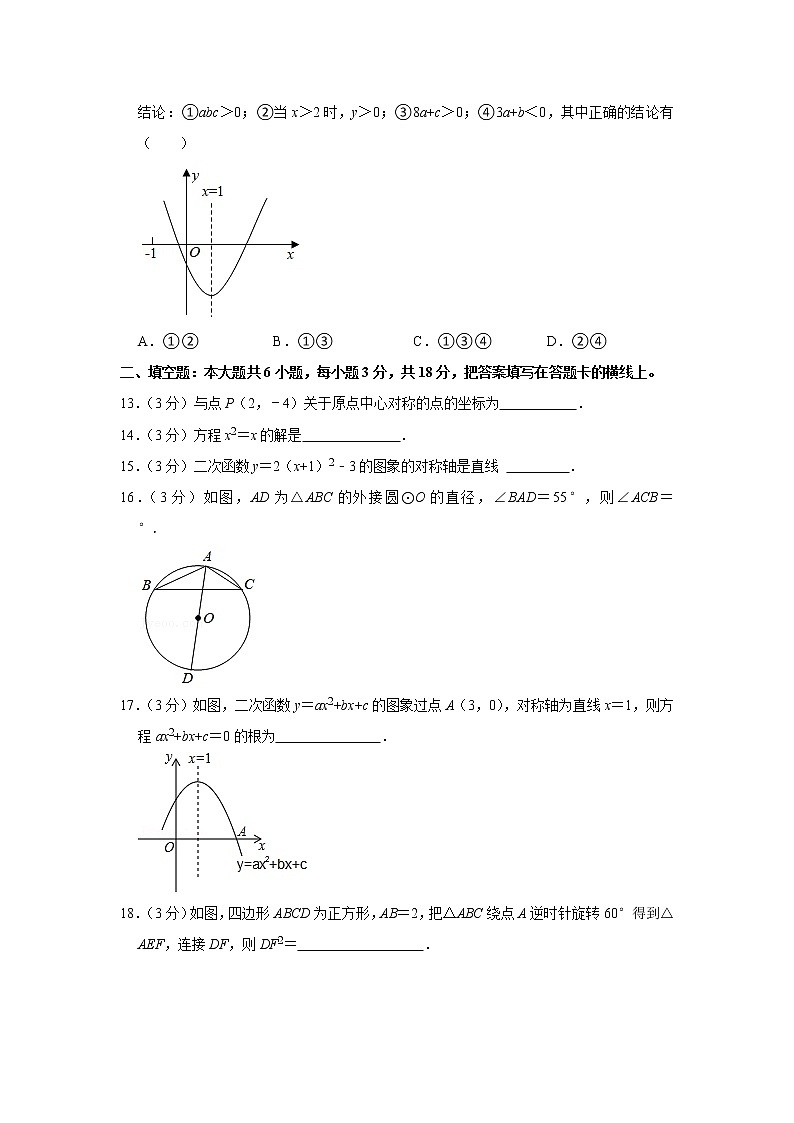
16.(3分)如图,AD为△ABC的外接圆⊙O的直径,∠BAD=55°,则∠ACB= °.
17.(3分)如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,则方程ax2+bx+c=0的根为 .
18.(3分)如图,四边形ABCD为正方形,AB=2,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF2= .
三、解答题:本大题共8小题,满分共66分。请将解答过程写在答题卡的相应位置上,解答应写出文字说明或演算步骤。
19.(6分)如图所示,△ABC是等边三角形,D是BC延长线上一点,△ACD经过旋转后到达△BCE的位置,
(1)旋转中心是 ,逆时针旋转了 度;
(2)如果M是AD的中点,那么经过上述旋转后,点M转到的位置为 .
20.(6分)二次函数y=ax2﹣2x+5与直线y=﹣2x+3交于点P(﹣1,b).
(1)求出此二次函数的解析式:
(2)求此二次函数的顶点坐标,并指出x取何值时,该函数的y随x的增大而减小.
21.(6分)如图,某石拱桥的桥拱呈“弓”形,其跨度AB=16m,拱的半径R=10m,求拱高CD.
22.(8分)已知x1,x2是一元二次方程2x2﹣2x+m+1=0的两个实数根.
(1)求实数m的取值范围;
(2)如果x1,x2满足不等式4+6x1x2>(x1+x2)2,且m为整数,求m的值.
23.(8分)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2;
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ;若P(a,b)为△ABC边上一点,则点P对应的点Q的坐标为 .
24.(10分)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费p(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
25.(10分)如图,已知CB是⊙O的弦,CD是⊙O的直径,A为CD延长线上一点,BC=AB,∠BAC=30°.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为2,求△CBD的面积.
26.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在点Q,且点Q在第一象限,使△BDQ中BD边上的高为?若存在,求出点Q的坐标;若不存在,请说明理由.
2020-2021学年广西玉林市福绵区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上。
1.(3分)下列电视台的台标,是中心对称图形的是( )
A. B.
C. D.
【解答】解:A、不是中心对称图形,故A选项不合题意;
B、不是中心对称图形,故B选项不合题意;
C、不是中心对称图形,故C选项不合题意;
D、是中心对称图形,故D选项符合题意.
故选:D.
2.(3分)一元二次方程x2+4x=2配方后化为( )
A.(x+2)2=6 B.(x﹣2)2=6 C.(x+2)2=﹣6 D.(x+2)2=﹣2
【解答】解:∵x2+4x=2,
∴x2+4x+4=2+4,
∴(x+2)2=6.
故选:A.
3.(3分)ʘO的半径为5cm,点A到圆心O的距离OA=4cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
【解答】解:∵⊙O的半径为5cm,点A到圆心O的距离为4cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内.
故选:B.
4.(3分)抛物线y=3x2先向下平移1个单位,再向左平移2个单位,所得的抛物线是( )
A.y=3(x+2)2﹣1 B.y=3(x﹣2)2+1
C.y=(x﹣2)2﹣1 D.y=3(x+2)2+1
【解答】解:抛物线y=3x2先向下平移1个单位,再向左平移2个单位后的抛物线顶点坐标为(﹣2,﹣1),
所得抛物线为y=3(x+2)2﹣1.
故选:A.
5.(3分)如图所示,平行四边形ABCD的对角线交于点O,下列结论错误的是( )
A.平行四边形ABCD是中心对称图形
B.△AOB≌△COD
C.△AOB≌△BOC
D.△AOB与△BOC的面积相等
【解答】解:A.平行四边形ABCD是中心对称图形,说法正确,故本选项不合题意;
B.△AOB≌△BOC,说法错误,故本选项不合题意;
C.∵四边形ABCD是平行四边形,
∴AB=CD,AO=CO,BO=DO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
故说法正确;
D.过B作BH⊥AC,
∵S△ABO=AO•BH,S△BOC=•BH,
∴△AOB与△BOC的面积相等,说法正确;
故选:B.
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
【解答】解:当x=1时,y1=﹣(1+1)2+2=﹣2,
当x=2时,y2=﹣(2+1)2+2=﹣7,
∴2>y1>y2.
故选:C.
7.(3分)将一个底面半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )
A.54° B.126° C.136° D.144°
【解答】解:∵将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,
∴圆锥侧面积公式为:S=πrl=π×6×15=90πcm2,
∴扇形面积为90π=,
解得:n=144,
∴侧面展开图的圆心角是144度.
故选:D.
8.(3分)在同一坐标系中,一次函数y=ax+2与二次函数y=x2﹣a的图象可能是( )
A. B.
C. D.
【解答】解:当a<0时,二次函数顶点在y轴正半轴,一次函数经过一、二、四象限;
当a>0时,二次函数顶点在y轴负半轴,一次函数经过一、二、三象限.
故选:A.
9.(3分)下列叙述正确的是( )
A.平分弦的直径必垂直于弦
B.三角形的外心到三边的距离相等
C.相等的圆心角所对的弧相等
D.垂直平分弦的直线必平分这条弦所对的弧
【解答】解:平分弦(不是直径)的直径必垂直于弦,A错误;
三角形的外心到三角形三个顶点的距离相等,B错误;
在同圆或等圆中,相等的圆心角所对的弧相等,C错误;
垂直平分弦的直线必平分这条弦所对的弧,D正确;
故选:D.
10.(3分)某商品原售价为60元,4月份下降了20%,从5月份起售价开始增长,6月份售价为75元,设5、6月份每个月的平均增长率为x,则x的值为( )
A.15% B.25% C.20% D.30%
【解答】解:设5、6月份每个月的平均增长率为x,
由题意,得60(1﹣20%)(1+x)2=75
解得x=0.25=25%(舍去负值)
故选:B.
11.(3分)将直角边长为3cm的等腰直角△ABC绕点A逆时针旋转15°后得到△AB'C',则图中阴影部分的面积( )
A. B.3 C.2 D.6cm2
【解答】解:设AB与B′C′交于D点,
根据旋转性质得∠CAC′=15°,而∠CAB=45°,
∴∠C′AD=∠CAB﹣∠CAC′=30°,
又∵AC′=AC=3cm,∠C′=∠C=90°,
∴C′D=AC′•tan30°=,
∴阴影部分的面积=×3×=cm2.
故选:A.
12.(3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,给出下列结论:①abc>0;②当x>2时,y>0;③8a+c>0;④3a+b<0,其中正确的结论有( )
A.①② B.①③ C.①③④ D.②④
【解答】解:∵函数开口方向向上,
∴a>0,
∵对称轴为直线x=1,即﹣=1,
∴b=﹣2a<0,
∵抛物线与y轴交点在y轴负半轴,
∴c<0,
∴abc>0,
故①正确,
由图象可知,当x=0时,y=c<0,由函数的对称性可知,x=2时,y=c<0,且当x>1时,y随x的增大而增大,
故②错误,
当x=﹣2时,y=4a﹣2b+c>0,即8a+c>0,
故③正确,
3a+b=a+b+2a=a>0,
故④错误,
综上,正确的是①③,
故选:B.
二、填空题:本大题共6小题,每小题3分,共18分,把答案填写在答题卡的横线上。
13.(3分)与点P(2,﹣4)关于原点中心对称的点的坐标为 (﹣2,4) .
【解答】解:根据中心对称的性质,得点P(2,﹣4)关于中心对称的点的坐标为(﹣2,4).
14.(3分)方程x2=x的解是 x1=0,x2=1 .
【解答】解:x2=x,
移项得:x2﹣x=0,
分解因式得:x(x﹣1)=0,
可得x=0或x﹣1=0,
解得:x1=0,x2=1.
故答案为:x1=0,x2=1
15.(3分)二次函数y=2(x+1)2﹣3的图象的对称轴是直线 x=﹣1 .
【解答】解:由y=2(x+1)2﹣3得,二次函数图象的对称轴为直线x=﹣1,
故答案为:x=﹣1.
16.(3分)如图,AD为△ABC的外接圆⊙O的直径,∠BAD=55°,则∠ACB= 35 °.
【解答】解:连接BD,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∵∠BAD=55°,
∴∠ADB=90°﹣55°=35°,
由圆周角定理得,∠ACB=∠ADB=35°,
故答案为:35.
17.(3分)如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,则方程ax2+bx+c=0的根为 x1=﹣1,x2=3 .
【解答】解:∵二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,
∴二次函数y=ax2+bx+c的图象与x轴的另一个交点为(﹣1,0),
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3.
故答案为x1=﹣1,x2=3.
18.(3分)如图,四边形ABCD为正方形,AB=2,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF2= 8﹣4 .
【解答】解:如图,连接BE,CE,过E作EG⊥BC于G,
由旋转可得,AB=AE=1=AD,AC=AF,∠BAC=∠EAF=45°=∠DAC,
∴∠CAE=∠FAD,
∴△ADF≌△AEC(SAS),
∴DF=CE,
由旋转可得,AB=AE=2,∠BAE=60°,
∴△ABE是等边三角形,
∴BE=2,∠ABE=60°,
∴∠EBG=30°,
∴EG=BE=1,BG=,
∴CG=2﹣,
∴Rt△CEG中,CE2=EG2+CG2=12+(2﹣)2=8﹣4,
∴DF2=8﹣4.
三、解答题:本大题共8小题,满分共66分。请将解答过程写在答题卡的相应位置上,解答应写出文字说明或演算步骤。
19.(6分)如图所示,△ABC是等边三角形,D是BC延长线上一点,△ACD经过旋转后到达△BCE的位置,
(1)旋转中心是 点C ,逆时针旋转了 60 度;
(2)如果M是AD的中点,那么经过上述旋转后,点M转到的位置为 BE的中点 .
【解答】解:(1)由△ACD经过旋转后到达△BCE的位置,
得,旋转中心是点C,逆时针旋转了60度,
故答案为:点C,60;
(2)如果M是AD的中点,那么经过上述旋转后,点M转到的位置为BE的中点;
故答案为:BE的中点.
20.(6分)二次函数y=ax2﹣2x+5与直线y=﹣2x+3交于点P(﹣1,b).
(1)求出此二次函数的解析式:
(2)求此二次函数的顶点坐标,并指出x取何值时,该函数的y随x的增大而减小.
【解答】解:(1)∵点P(﹣1,b)在直线y=﹣2x+3上,
∴b=2+3=5,
∴P(﹣1,5),
把P(﹣1,5)代入y=ax2﹣2x+5,得到a=﹣2,
∴二次函数的解析式为y=﹣2x2﹣2x+5.
(2)∵y=﹣2(x+)2+,
∴顶点坐标为(﹣,),对称轴为x=﹣
∵a<0,
∴当x>﹣时,y随x的增大而减小.
21.(6分)如图,某石拱桥的桥拱呈“弓”形,其跨度AB=16m,拱的半径R=10m,求拱高CD.
【解答】解:如图所示:作OD⊥AB交于C,垂足为D,
根据垂径定理,AD=BD=×16=8m,
设CD=xm,则OD=(10﹣x)m,
根据勾股定理得:82+(10﹣x)2=102,
解得:x=4或16(舍去),
故拱高CD为4m.
22.(8分)已知x1,x2是一元二次方程2x2﹣2x+m+1=0的两个实数根.
(1)求实数m的取值范围;
(2)如果x1,x2满足不等式4+6x1x2>(x1+x2)2,且m为整数,求m的值.
【解答】解:(1)∵方程2x2﹣2x+m+1=0有两个实数根,
∴Δ≥0,
即(﹣2)2﹣4×2(m+1)≥0,
解得m≤.
故实数m的取值范围是m≤;
(2)∵x1,x2是一元二次方程2x2﹣2x+m+1=0的两个实数根,
∴x1+x2=1,x1•x2=(m+1),
∵4+6x1x2>(x1+x2)2,
∴4+6×(m+1)>12,
解得m>﹣2,
∵m≤且m为整数,
∴m的值为﹣1或0.
23.(8分)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2;
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 (4,2) ;若P(a,b)为△ABC边上一点,则点P对应的点Q的坐标为 (b,﹣a) .
【解答】解:(1)如图.
(2)由图形可得:A2坐标为(4,2),Q的坐标为(b,﹣a),
故答案为:(4,2);(b,﹣a)
24.(10分)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费p(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
【解答】解:(1)由题意得:
y=60﹣(2分)
(2)p=(200+x)(60﹣)=﹣+40x+12000(3分)
(3)w=(200+x)(60﹣)﹣20×(60﹣)(2分)
=﹣+42x+10800
=﹣(x﹣210)2+15210
当x=210时,w有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时,w有最大值,且最大值是15210元.
25.(10分)如图,已知CB是⊙O的弦,CD是⊙O的直径,A为CD延长线上一点,BC=AB,∠BAC=30°.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为2,求△CBD的面积.
【解答】解:(1)如图,连接OB,
∵BC=AB,
∴∠BCA=∠BAC=30°,
∵CD是⊙O的直径,
∴∠CBD=90°,
∴∠BDC=90°﹣30°=60°,
∵OB=OD,
∴∠OBD=∠ODB=60°,
∵∠ABD=∠ODB﹣∠A=60°﹣30°=30°,
∴∠OBD+∠ABD=60°+30°=90°,
即OB⊥AB,
∵OB是⊙O半径,
∴AB是⊙O的切线;
(2)在Rt△BCD中,∠BCD=30°,CD=2OC=4,
∴BC=CD=2,BC=CD=2,
∴S△BCD=BC•BD=×2×2=2.
26.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在点Q,且点Q在第一象限,使△BDQ中BD边上的高为?若存在,求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3;
(2)设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∴当m=,PM有最大值;
(3)如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,
设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为时,即QH=HG=,
∴QG==2,
∵点Q在第一象限,
∴﹣x2+3x=2,
解得x=1或x=2,
∴Q(1,4)或(2,3),
综上可知存在满足条件的点Q,其坐标为(1,4)或(2,3).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/10/24 11:02:24;用户:教师17;邮箱:zybang17@xyh.com;学号:38915552
人教版七年级下学期期中数学模拟测试卷2: 这是一份人教版七年级下学期期中数学模拟测试卷2,共8页。试卷主要包含了选择题,填空题,计算题等内容,欢迎下载使用。
人教版九年级上册数学期中测试卷(附答案): 这是一份人教版九年级上册数学期中测试卷(附答案),共9页。
人教版九年级上册数学期中测试卷附答案答题卡: 这是一份人教版九年级上册数学期中测试卷附答案答题卡,共3页。试卷主要包含了答题前,考生先将自己的姓名,保持卡面清洁,不要折叠等内容,欢迎下载使用。












