一轮复习专题2.6 指数函数与对数函数（二）（解析版）教案

06指数函数与对数函数(二)

一、必备知识:

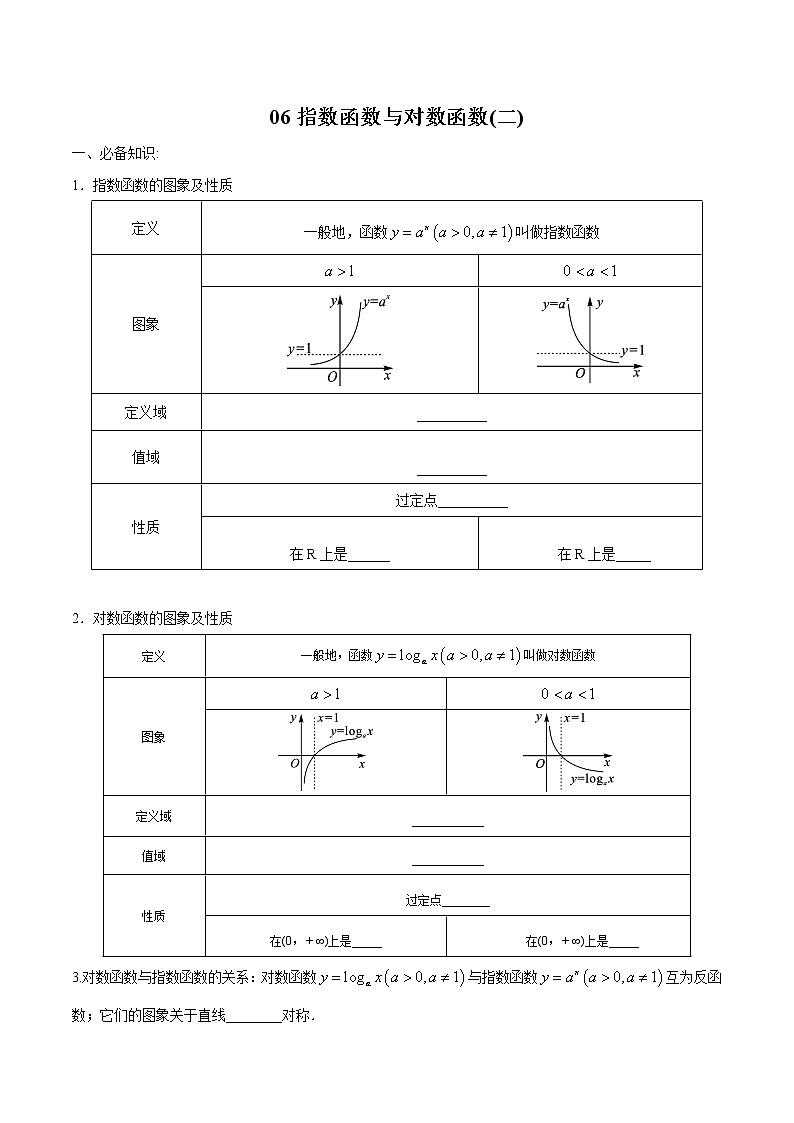
1．指数函数的图象及性质

2．对数函数的图象及性质

3.对数函数与指数函数的关系：对数函数与指数函数互为反函数；它们的图象关于直线________对称．

自查自纠：

1.R　(0，＋∞)　(0，1)　增函数　减函数  2．(0，＋∞)　R　(1，0)　增函数　减函数

3．y＝x

二、题型训练：

题组一：

1 ．函数的值域为______．

【答案】

【解析】令，则，当时，；当时，；故函数，的值域为．故答案为：[-4，0]．

2．已知函数，，则的最小值为__________.

【答案】0.

【解析】由题可得将函数化简为：，设，则，因为，所以.根据二次函数的性质得到：当时，取得最小值.

3．定义在上的偶函数，当时，，则的值域为______．

【答案】

【详解】由题意，函数是定义在上的偶函数，所以，即，当时，，所以.又由是定义在上的偶函数，所以函数的图象关于y轴对称，所以的值域为.

4．函数的值域为               .

【答案】

【解析】由得,所以函数的定义域是，设点，

，所以.

课堂检测：

5．已知，则函数的最大值为__________．

【答案】

【解析】 令 ，则

即 又∵对称轴 ∴当 即 时

6．若函数的定义域为，则函数的值域为__________.

【答案】

【详解】由，得，，∴，∴.令，则，∴当时，；当时，.

7．函数的值域为______________

【答案】［－3，9］

【详解】设，∵，∴，则可化为，其对称轴为，时，，时，，

∴函数的值域为．故答案为．

8．设函数f（x）=log3•log3（9x），且，则函数f（x）的值域为___．

【答案】[-]

【详解】f（x）=（log3x-1）（2+log3x）=；∵；

∴∴时，f（x）取最小值-；log3x=3时，f（x）取最大值10；

∴函数f（x）的值域为[-]

题组二

9．函数的单调递减区间为（　　）

A． B． C． D．

【答案】B

由函数，结合复合函数单调性知识可知，它的减区间，即为的增区间．由二次函数的性质可得的增区间为，故选：B．

10．函数的单调递增区间是（　　）

A． B． C． D．

【答案】D

【解析】因为，是指数函数，是增函数，是开口向下的二次函数，所以时，二次函数是增函数， 时，是减函数，由复合函数的单调性可知：函数的单调递增区间是．故选：D．

11．函数的单调增区间是______．

【答案】[1，2]

【解析】函数f（x）＝（）的单调增区间，即y 的减区间，即t＝﹣x2+2x在t≥0时的减区间．再利用二次函数的性质可得t＝﹣x2+2x在t≥0时的减区间 为[1，2]．

12．函数的单调递增区间为（   ）

A． B． C． D．

【答案】D

【详解】由题意，函数的定义域为，设 ，

则在上单调递减，在上单调递增，又因为在上单调递增，根据复合函数的单调性，可得函数的单调递增区间为.

课堂检测：

13．函数y=（）的单调递增区间是（　　）

A． B． C． D．

【答案】C

【详解】y=，设t=x2+4x-3，则y=3t是增函数，求函数y的单调递增区间，等价为求函数设t=x2+4x-3的单调递增区间，函数t=x2+4x-3的对称轴为x=-2，则[-2，+∞）上是增函数，则y=的单调递增区间是[-2，+∞），故选：C．

14．已知的单调递增区间是                     .

【答案】

15．函数，的单调递增区间为__________．

【答案】(－∞，1]

【解析】法一：f(x)＝x在定义域上为减函数，故要求f(x)的单调递增区间，只需求y＝|x－1|的单调递减区间．又因为y＝|x－1|的单调递减区间为(－∞，1]，所以f(x)的单调递增区间为(－∞，1]．

法二：f(x)＝可画出f(x)的图象求其单调递增区间．答案：(－∞，1].

题组三：

16．函数的单调递减区间是______________．

【答案】．

【详解】函数定义域为，是减函数，而在上是增函数，在上是减函数．∴的减区间．故答案为．

17．已知函数，则函数的单调递增区间是__________________。

【答案】

【详解】因为函数，所以所以或，令由二次函数性质可知：当时，单调递减；当时，单调递增，故当时，函数单调递增，故函数的单调递增区间是。

18．的单调递增区间是              ．

【答案】

【解析】函数的定义域为，设，函数在为减函数，则在为减函数，且当时，，当时，，故的单调递增区间是

19．函数f(x)＝log(x＋1)(2x－1)的单调递增区间是______．

【答案】

【详解】应该满足：,所以，即定义域为此时∴函数f(x)＝log(x＋1)(2x－1)的单调递增区间故答案为：

课堂检测：

20．的单调递增区间为_______________．

【答案】

【详解】定义域：-5<x<1令g（x）=

函数g（x）对称轴是x=-2，单调递增区间是则函数f（x）单调递增区间是

21．函数的单调递减区间是 _____．

【答案】

【详解】即或，函数的定义域为，在定义域内函数的增区间是，因为递减，在上递增，函数的单调递减区间为，故答案为.

22．函数的单调递减区间是               。

【答案】

【解析】由得：此时在上是增函数；由得：，即此时在上是减函数.

题组四：

23．若函数在区间内单调递增，则实数的取值范闱为______．

【答案】

【解析】根据对数函数的定义可得，解得，因为二次函数图象的对称轴为，由复合函数单调性可得函数的单调递增区间为，要使函数在区间内单调递增，只需，解关于的不等式组得，即的取值范围是，故答案为.

24．已知函数在上单调递减，则的取值范围是____________.

【答案】

【详解】若函数y=log2（ax﹣1）在（﹣2，﹣1）上单调递减，则a＜0且ax﹣1＞0在（﹣2，﹣1）恒成立，即a＜在（﹣2，﹣1）恒成立，故a≤﹣1，故答案为：a≤﹣1

25．已知在区间上是增函数，则实数a的取值范围是______．

【答案】

【解析】令．在上为增函数，应在上为减函数且在上恒成立．因此，即．

解得，故实数的取值范围是．

26．若函数（且）在[1,3]上单调递增，则的取值范围是__________．

【答案】

【解析】令，因为，所以为增函数，因为函数（且）在[1,3]上单调递增，所以，解得；故填.

课堂检测：

27．已知在上是增函数，则的取值范围是______．

【答案】

【详解】由可得，令，，当时，为增函数；当时，为减函数.故即.

28．若函数在区间上是增函数，则的取值范围是_____

【答案】

【详解】令，其开口向上，对称轴为，要使在区间上是增函数，由，解得.

29．函数在区间上是单调增函数，则的取值范围是____________．

【答案】

【解析】设，则，要使函数在区间上是单调增函数，由复合函数单调性的判定方法可知与同为增函数或同为减函数时才能满足，故有或，所以．

三、课外作业：

1．函数的值域是________.

【答案】

【解析】令，因为，所以。

2．已知函数，则函数的值域为__________

【答案】

【详解】 ,当时，，当时，，函数，则函数的值域为.

3．函数的值域为________.

【答案】

【详解】，且    值域为：

4．函数的最小值是___．

【答案】1

【详解】令，，则，所以，即所求最小值为1.故答案为：1.

5．函数的单调递减区间为_____.

【答案】

【解析】由，解得 ，可得：函数的定义域为 由函数 ，∴函数的单调递减区间为.

6．函数的单调递减区间是______．

【答案】

【详解】令，由得，又，∴在递增，在上递减，又是增函数，

∴的单调递增区间．故答案为．

7．函数的单调递减区间是______．

【答案】

【解析】对于函数，它的单调递减区间，即时的单调减区间，而时的单调减区间为.故答案为：．

8．函数的单调递减区间为_____________.

【答案】

【详解】由得-,因为，所以求在上单调增区间，为.

9．已知在区间[2，＋∞)上为减函数，则实数的取值范围是___________.

【答案】﹣4＜a≤4

【详解】令t=x2﹣ax+3a，则由函数f（x）=g（t）= 在区间[2，+∞）上为减函数，可得函数t在区间[2，+∞）上为增函数且t（2）＞0，故有，解得﹣4＜a≤4．

10．已知y=loga（3a-a2x）在[0，2]上为x的减函数，则a的取值范围为______．

【答案】（1，）

【详解】∵y＝loga（3a﹣a2x）在[0，2]上为x的减函数，∵t＝3a﹣a2x 在[0，2]上为x的减函数，故有，求得1＜a，故当a的取值范围为（1，），故答案为：（1，）．