初中湘教版3.4 相似三角形的判定与性质课后作业题

这是一份初中湘教版3.4 相似三角形的判定与性质课后作业题，共10页。

一、选择题
1.△ABC的三边长分别为9，6，12，△DEF的三边长分别为4，6，x (其中x≥6)，若△ABC∽△DEF，则x的值为( )
A．7 B．8 C．9 D．10
2.已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF的一边长为4 cm，当△DEF的另两边长是下列( )组时，这两个三角形相似．
A．2 cm，3 cm B．4 cm，5 cm C．5 cm，6 cm D．6 cm，7 cm
3.【2020·玉林】一个三角形木架三边长分别是75 cm，100 cm，120 cm，现要再做一个与其相似的三角形木架，而只有长为60 cm和120 cm的两根木条．要求以其中一根为一边，从另一根截下两段作为另两边(允许有余料)，则不同的截法有( )
A．一种 B．两种 C．三种 D．四种
4.如图，点D，E，F为△ABC的三边AB，BC，AC的中点，连接DE，EF，DF，则下列结论不正确的是( )
A．DE∥AC B．eq \f(DE,AC)＝eq \f(DF,BC)＝eq \f(EF,AB)＝eq \f(1,2) C．△DEF∽△CAB D．DF＝EF

第4题图 第5题图 第9题图 第11题图
5.如图，O为△ABC内任意一点，点A′，B′，C′分别是线段OA，OB，OC的中点，判定△A′B′C′与△ABC相似的条件是( )
A.eq \f(A′B′,AB)＝eq \f(B′C′,BC)＝eq \f(A′C′,AC)＝eq \f(1,2) B.eq \f(A′B′,AB)＝eq \f(B′C′,BC)＝eq \f(1,2) C.eq \f(B′C′,BC)＝eq \f(A′C′,AC)＝eq \f(1,2) D.eq \f(A′B′,AB)＝eq \f(A′C′,AC)＝eq \f(1,2)
6.在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，要使Rt△ABC和Rt△DEF相似，只要( )
A．BC∶DE＝AB∶EF B．AB∶DE＝BC∶EF
C．AB·DE＝BC·EF D．AB∶DF＝BC∶DE
7.在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列各组的条件不能判定这两个三角形相似的是( )
A．∠A＝65°，∠D＝25°
B．AC＝3，BC＝4，DF＝6，DE＝10
C．AC＝9，BC＝12，DF＝12，EF＝16
D．AB＝10，AC＝8，DF＝20，EF＝16
8.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形的三条边长分别是3，4及x，那么x的值( )
A．只有1个 B．可以有2个 C．可以有3个 D．有无数个
9.如图，在△ABC中，∠ABC＝90°，BD∶AC＝DE∶CB，其中DE⊥BC，垂足为E点，则图中与△ABC相似的三角形有( )
A．4个 B．3个 C．2个 D．1个
10.如图，在正方形网格(每个小正方形的边长为1)中，三角形顶点都在小正方形的顶点上，我们称为“格点三角形”，其中格点三角形是相似三角形的为( )
A．①③ B．①② C．②③ D．②④
11.如图，已知∠ACB＝∠ADC＝90°，AD＝2，CD＝2，当△ACB∽△ADC时，AB的长为( )
A．4 B．2 eq \r(2) C．3 eq \r(2) D．6
12.【2020·大庆】已知两个直角三角形的三边长分别为3，4，m和6，8，n，且这两个直角三角形不相似，则m＋n的值为( )
A．10＋eq \r(7)或5＋2eq \r(7) B．15 C．10＋eq \r(7) D．15＋3eq \r(7)
二、填空题
13.三边________的两个三角形相似；斜边与直角边对应成比例的两个直角三角形______．
14.如图是由4个边长为1的正方形组成的图形，∠ABC＝ .

第14题图 第18题图
15.若△ABC的三边长分别为2,2,5,△DEF的三边长分别为10,2,22,则△ABC与△DEF .(填“相似”或“不相似”)
16.在△ABC和△A1B1C1中,AB=12 cm,AC=15 cm,BC=21 cm,A1B1=16 cm,B1C1=28 cm,当A1C1= cm时,△ABC∽△A1B1C1.
17.在△ABC中,AB∶BC∶CA=3∶5∶7.在△DEF中,若DE=6 cm,且EF18.如图,把一张4×3的方格纸放在平面直角坐标系内,每个方格的边长为1个单位,△ABC的顶点都在方格的格点位置,即点A的坐标是(1,0).若点D也在格点位置(与点A不重合),且△DBC与△ABC相似,则符合条件的点D的坐标是 .
三、解答题
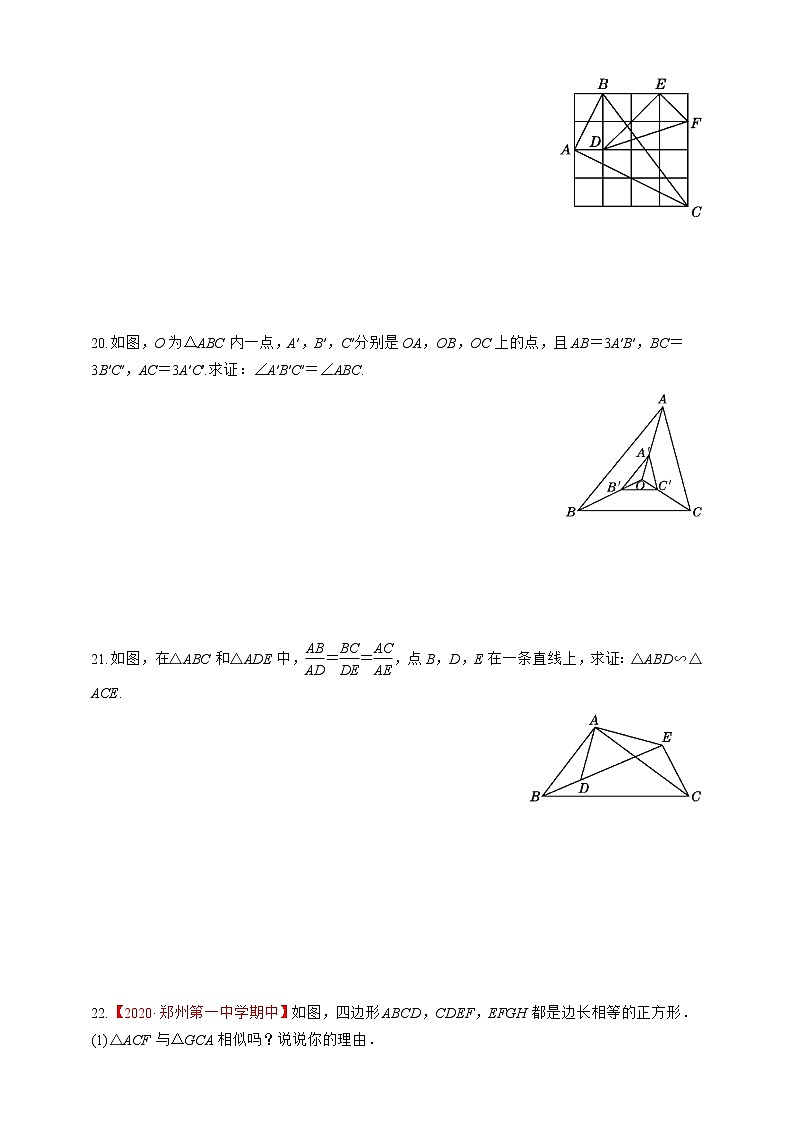
19.如图，已知4×4的方格中的△ABC与△DEF，∠ABC与∠DFE相等吗？说明理由．
20.如图，O为△ABC内一点，A′，B′，C′分别是OA，OB，OC上的点，且AB＝3A′B′，BC＝3B′C′，AC＝3A′C′.求证：∠A′B′C′＝∠ABC.
21.如图，在△ABC和△ADE中，eq \f(AB,AD)＝eq \f(BC,DE)＝eq \f(AC,AE)，点B，D，E在一条直线上，求证：△ABD∽△ACE.
22.【2020·郑州第一中学期中】如图，四边形ABCD，CDEF，EFGH都是边长相等的正方形．
(1)△ACF与△GCA相似吗？说说你的理由．
(2)求∠1＋∠2的度数．
23.如图1,点O在△ABC内部,连接AO,BO,CO,点A',B',C'分别在AO,BO,CO上,且AB∥A'B',BC∥B'C'.
(1)求证:△ABC∽△A'B'C'.
(2)将点O移至△ABC外,如图2,补充图形.若其他条件不变,题中要求证的结论还成立吗?如果成立,请换一种判定方法证明结论.
24.【中考·菏泽】如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：
(1)试证明△ABC为直角三角形；
(2)判断△ABC和△DEF是否相似，并说明理由；
(3)画一个三角形，使它的三个顶点为P1，P2，P3，P4，P5中的3个格点且与△ABC相似，并说明理由．
参考答案
一、选择题
1.△ABC的三边长分别为9，6，12，△DEF的三边长分别为4，6，x (其中x≥6)，若△ABC∽△DEF，则x的值为( B )
A．7 B．8 C．9 D．10
2.已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF的一边长为4 cm，当△DEF的另两边长是下列( C )组时，这两个三角形相似．
A．2 cm，3 cm B．4 cm，5 cm C．5 cm，6 cm D．6 cm，7 cm
3.【2020·玉林】一个三角形木架三边长分别是75 cm，100 cm，120 cm，现要再做一个与其相似的三角形木架，而只有长为60 cm和120 cm的两根木条．要求以其中一根为一边，从另一根截下两段作为另两边(允许有余料)，则不同的截法有( B )
A．一种 B．两种 C．三种 D．四种
【点拨】分类讨论：长120 cm的木条与三角形木架的最长边相等，则长120 cm的木条不能作为一边，设从120 cm的一根上截下的两段长分别为x cm，y cm(x＜y，x＋y≤120)，易得长60 cm的木条不能与75 cm的一边对应，所以当长60 cm的木条与100 cm的一边对应时有eq \f(x,75)＝eq \f(y,120)＝eq \f(60,100)；当长60 cm的木条与120 cm的一边对应时有eq \f(x,75)＝eq \f(y,100)＝eq \f(60,120)，然后分别利用比例的性质计算出两种情况下x和y的值．
4.如图，点D，E，F为△ABC的三边AB，BC，AC的中点，连接DE，EF，DF，则下列结论不正确的是( D )
A．DE∥AC B．eq \f(DE,AC)＝eq \f(DF,BC)＝eq \f(EF,AB)＝eq \f(1,2) C．△DEF∽△CAB D．DF＝EF

第4题图 第5题图 第9题图 第11题图
5.如图，O为△ABC内任意一点，点A′，B′，C′分别是线段OA，OB，OC的中点，判定△A′B′C′与△ABC相似的条件是( A )
A.eq \f(A′B′,AB)＝eq \f(B′C′,BC)＝eq \f(A′C′,AC)＝eq \f(1,2) B.eq \f(A′B′,AB)＝eq \f(B′C′,BC)＝eq \f(1,2) C.eq \f(B′C′,BC)＝eq \f(A′C′,AC)＝eq \f(1,2) D.eq \f(A′B′,AB)＝eq \f(A′C′,AC)＝eq \f(1,2)
6.在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，要使Rt△ABC和Rt△DEF相似，只要( B )
A．BC∶DE＝AB∶EF B．AB∶DE＝BC∶EF
C．AB·DE＝BC·EF D．AB∶DF＝BC∶DE
7.在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列各组的条件不能判定这两个三角形相似的是( D )
A．∠A＝65°，∠D＝25°
B．AC＝3，BC＝4，DF＝6，DE＝10
C．AC＝9，BC＝12，DF＝12，EF＝16
D．AB＝10，AC＝8，DF＝20，EF＝16
8.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形的三条边长分别是3，4及x，那么x的值( B )
A．只有1个 B．可以有2个 C．可以有3个 D．有无数个
9.如图，在△ABC中，∠ABC＝90°，BD∶AC＝DE∶CB，其中DE⊥BC，垂足为E点，则图中与△ABC相似的三角形有( A )
A．4个 B．3个 C．2个 D．1个
10.如图，在正方形网格(每个小正方形的边长为1)中，三角形顶点都在小正方形的顶点上，我们称为“格点三角形”，其中格点三角形是相似三角形的为( A )
A．①③ B．①② C．②③ D．②④
【点拨】设网格中每个小正方形的边长为1.由题图得①中的三角形的各边长分别为2，eq \r(2)，eq \r(10)，③中的三角形的各边长分别为2eq \r(2)，2，2eq \r(5)，∵eq \f(2,2\r(2))＝eq \f(\r(2),2)＝eq \f(\r(10),2\r(5))，∴两个三角形的三边对应成比例，∴①和③相似．故选A.
11.如图，已知∠ACB＝∠ADC＝90°，AD＝2，CD＝2，当△ACB∽△ADC时，AB的长为( A )
A．4 B．2 eq \r(2) C．3 eq \r(2) D．6
12.【2020·大庆】已知两个直角三角形的三边长分别为3，4，m和6，8，n，且这两个直角三角形不相似，则m＋n的值为( A )
A．10＋eq \r(7)或5＋2eq \r(7) B．15 C．10＋eq \r(7) D．15＋3eq \r(7)
【点拨】当3，4为直角边长，6，8也为直角边长时，两三角形相似，不合题意；当三边长分别为3，4，eq \r(7)和6，8，2eq \r(7)时，两三角形相似，不合题意．当3，4为直角边长时，m＝5；则8为另一三角形的斜边长，其中一直角边长为eq \r(82－62)＝2eq \r(7)，故m＋n＝5＋2eq \r(7)；当6，8为直角边长时，n＝10；则4为另一三角形的斜边长，其中一直角边长为eq \r(42－32)＝eq \r(7)，故m＋n＝10＋eq \r(7)；故选A.
二、填空题
13.三边________的两个三角形相似；斜边与直角边对应成比例的两个直角三角形______．
【答案】成比例 相似
14.如图是由4个边长为1的正方形组成的图形，∠ABC＝ .
【答案】45°

第14题图 第18题图
15.若△ABC的三边长分别为2,2,5,△DEF的三边长分别为10,2,22,则△ABC与△DEF .(填“相似”或“不相似”)
【答案】相似
16.在△ABC和△A1B1C1中,AB=12 cm,AC=15 cm,BC=21 cm,A1B1=16 cm,B1C1=28 cm,当A1C1= cm时,△ABC∽△A1B1C1.
【答案】20
17.在△ABC中,AB∶BC∶CA=3∶5∶7.在△DEF中,若DE=6 cm,且EF【答案】3∶5或3∶7或5∶7
【提示】本题由于相似三角形的对应边没有唯一确定,所以分三种情况,DE可能对应AB,也可能对应BC,也可能对应CA.又因为EF18.如图,把一张4×3的方格纸放在平面直角坐标系内,每个方格的边长为1个单位,△ABC的顶点都在方格的格点位置,即点A的坐标是(1,0).若点D也在格点位置(与点A不重合),且△DBC与△ABC相似,则符合条件的点D的坐标是 .
【答案】(0,0)或(3,2)或(3,3)或(4,1)
三、解答题
19.如图，已知4×4的方格中的△ABC与△DEF，∠ABC与∠DFE相等吗？说明理由．
解：相等．理由如下：设每个小方格的边长为1，
则AB＝eq \r(5)，AC＝2 eq \r(5)，BC＝5，
EF＝eq \r(2)，ED＝2 eq \r(2)，DF＝eq \r(10).
∴AB∶EF＝AC∶ED＝BC∶DF＝eq \r(5)∶eq \r(2).
∴△ABC∽△EFD. ∴∠ABC＝∠DFE.
20.如图，O为△ABC内一点，A′，B′，C′分别是OA，OB，OC上的点，且AB＝3A′B′，BC＝3B′C′，AC＝3A′C′.求证：∠A′B′C′＝∠ABC.
证明：∵AB＝3A′B′，BC＝3B′C′，
AC＝3A′C′，
∴A′B′∶AB＝B′C′∶BC＝A′C′∶AC＝1∶3.
∴△A′B′C′∽△ABC.
∴∠A′B′C′＝∠ABC.
21.如图，在△ABC和△ADE中，eq \f(AB,AD)＝eq \f(BC,DE)＝eq \f(AC,AE)，点B，D，E在一条直线上，求证：△ABD∽△ACE.
证明：∵在△ABC和△ADE中，eq \f(AB,AD)＝eq \f(BC,DE)＝eq \f(AC,AE)，
∴△ABC∽△ADE，∴∠BAC＝∠DAE，
∴∠BAD＝∠CAE.
∵eq \f(AB,AD)＝eq \f(AC,AE)，∴eq \f(AD,AE)＝eq \f(AB,AC)，∴△ABD∽△ACE.
22.【2020·郑州第一中学期中】如图，四边形ABCD，CDEF，EFGH都是边长相等的正方形．
(1)△ACF与△GCA相似吗？说说你的理由．
解：△ACF与△GCA相似．理由：可设正方形ABCD，CDEF，EFGH的边长为a，则△ACF的三边长分别为AC＝eq \r(2)a，CF＝a，AF＝eq \r(5)a，△GCA的三边长分别为AC＝eq \r(2)a，CG＝2a，AG＝eq \r(10)a.
∴eq \f(CF,CA)＝eq \f(a,\r(2)a)＝eq \f(\r(2),2)，eq \f(AC,GC)＝eq \f(\r(2)a,2a)＝eq \f(\r(2),2)，eq \f(AF,GA)＝eq \f(\r(5)a,\r(10)a)＝eq \f(\r(2),2).
∴eq \f(CF,CA)＝eq \f(AC,GC)＝eq \f(AF,GA)，∴△ACF与△GCA相似．
(2)求∠1＋∠2的度数．
解：∵△ACF∽△GCA，∴∠1＝∠CAF.
∴∠1＋∠2＝∠CAF＋∠2＝∠ACB＝45°.
23.如图1,点O在△ABC内部,连接AO,BO,CO,点A',B',C'分别在AO,BO,CO上,且AB∥A'B',BC∥B'C'.
(1)求证:△ABC∽△A'B'C'.
(2)将点O移至△ABC外,如图2,补充图形.若其他条件不变,题中要求证的结论还成立吗?如果成立,请换一种判定方法证明结论.
证明:(1)∵AB∥A'B',BC∥B'C',
∴△OA'B'∽△OAB,△OB'C'∽△OBC,∠A'B'C'=∠ABC,∴OB'OB=A'B'AB=B'C'BC,
∴△A'B'C'∽△ABC.
(2)补充图形如图所示,(1)中的结论仍成立,证明如下:
∵AB∥A'B',BC∥B'C',
∴OB'OB=OA'OA=OC'OC,且∠A'OC'=∠AOC,
∴△OA'C'∽△OAC,∴A'C'∥AC.
根据平行线的性质,得∠ABC=∠A'B'C',∠BAC=∠B'A'C',∠ACB=A'C'B',
∴△A'B'C'∽△ABC.
24.【中考·菏泽】如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：
(1)试证明△ABC为直角三角形；
证明：根据勾股定理，
得AB＝2 eq \r(5)，AC＝eq \r(5)，BC＝5，
显然有AB2＋AC2＝BC2，∴△ABC为直角三角形．
(2)判断△ABC和△DEF是否相似，并说明理由；
解：△ABC和△DEF相似．
理由如下：根据勾股定理，
得DE＝4 eq \r(2)，DF＝2 eq \r(2)，EF＝2 eq \r(10).
又∵AB＝2 eq \r(5)，AC＝eq \r(5)，BC＝5，
∴eq \f(AB,DE)＝eq \f(AC,DF)＝eq \f(BC,EF)＝eq \f(\r(10),4).
∴△ABC∽△DEF.
(3)画一个三角形，使它的三个顶点为P1，P2，P3，P4，P5中的3个格点且与△ABC相似，并说明理由．
解：如图，连接P2P5，P2P4，P4P5，则△P2P4P5符合要求．
理由如下：由勾股定理，得P2P5＝eq \r(10)，P2P4＝eq \r(2)，P4P5＝2 eq \r(2).
又∵AB＝2eq \r(5)，AC＝eq \r(5)，BC＝5，
∴eq \f(P2P5,BC)＝eq \f(P4P5,AB)＝eq \f(P2P4,AC)＝eq \f(\r(10),5).
∴△ABC∽△P4P5P2.