2022年中考数学二轮复习专题《相似三角形》课件PPT

这是一份2022年中考数学二轮复习专题《相似三角形》课件PPT，共27页。PPT课件主要包含了比例线段的性质，对应角，相似比，相似比的平方，第1题图，第2题图，第4题图，相似多边形的性质，成比例，教材母题1题图等内容，欢迎下载使用。
相似三角形的性质及判定
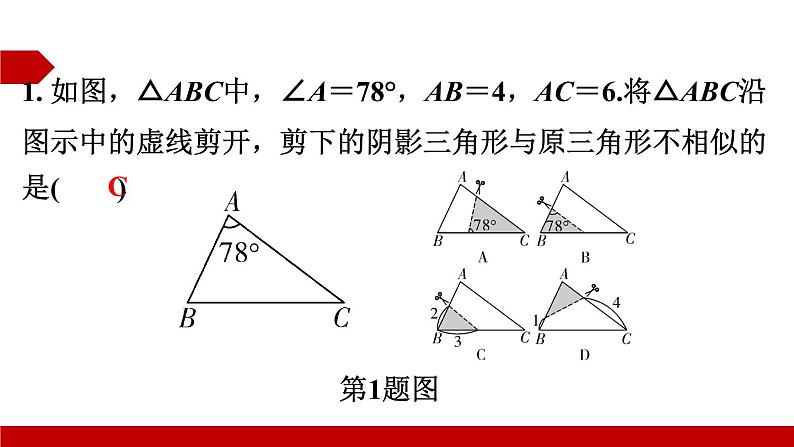
1. 如图，△ABC中，∠A＝78°，AB＝4，AC＝6.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是(　　)
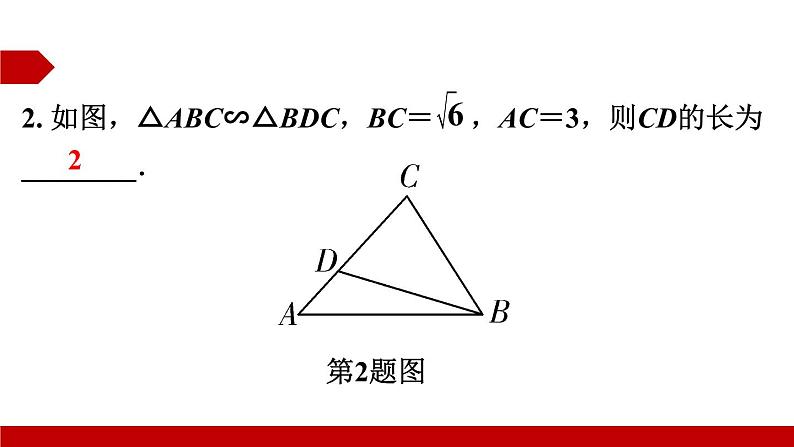
2. 如图，△ABC∽△BDC，BC＝ ，AC＝3，则CD的长为________．　
3. 若△ABC与△DEF相似且面积之比为25∶16，则△ABC与△DEF的周长之比为________．4. 如图，在△ABC中，E，F分别是边AB，AC上的点，且满足 则△AEF与△ABC的面积比是________.
【解析】∵ ，∴ ，又∵∠A＝∠A，∴△AEF∽△ABC，∴△AEF与△ABC的面积比为1∶9.
性质：(1)相似多边形的对应角⑨______，对应边⑩______；(2)相似多边形的周长比等于 ________，面积比等于 ____________．已知两个五边形的相似比为2∶5，则这两个五边形的周长比为________.
教材母题1(人教九下43页习题12)如图，平行于BC的直线DE把△ABC分成面积相等的两部分，试确定点D(或E)的位置．
解：∵DE∥BC，∴△ADE∽△ABC，∵S△ADE＝S四边形DBCE，∴S△ADE∶S△ABC＝1∶2，∵S△ADE∶S△ABC＝(AD∶AB)2，∴AD∶AB＝1∶ .
【还能这样考】1. 如图，在△ABC中，BC＝10，D、E、H分别在AB、AC、BC边上，且DE∥BC，EH∥AB，若S△ADE∶S四边形DBCE＝1∶3，求CH的长．
解：∵DE∥BC，∴△ADE∽△ABC，∵S△ADE∶S四边形DBCE＝1∶3，∴S△ADE∶S△ABC＝1∶4＝(AE∶AC)2，∴AE∶AC＝1∶2，∴CE∶CA＝1∶2，∵EH∥AB，∴CH∶CB＝CE∶CA＝1∶2，∴CH＝ BC＝5.
2. 如图，在△ABC中，AB＝6，D、F在AB上，E、G在AC上，且DE∥FG∥BC，DE，FG把△ABC分成三部分，面积记为S1，S2，S3，若S1∶S2∶S3＝1∶3∶5，求AD、DF的长．
解：∵DE∥FG∥BC，∴△ADE∽△AFG∽△ABC，∵S1∶S2∶S3＝1∶3∶5，∴S△ADE∶S△AFG∶S△ABC＝1∶4∶9，∴AD∶AF∶AB＝1∶2∶3，∴AD＝ AB＝2，AF＝ AB＝4，∴DF＝AF－AD＝4－2＝2.即AD的长为2，DF的长为2.
3. 如图，在△ABC中，P为△ABC内一点，过点P分别作MH∥AB，FG∥AC，DE∥BC，记△DPF、△PME、△PHG的面积分别为S1，S2，S3，若S1＝4，S2＝9，S3＝25，求△ABC的面积．
3. 解：∵MH∥AB，FG∥AC，DE∥BC，∴△PDF∽△EPM∽△GHP∽△CBA，四边形BDPH，CEPG均为平行四边形，∴DP＝BH，PE＝CG，∵S1＝4，S2＝9，S3＝25，∴DP∶PE∶HG＝2∶3∶5，设DP＝BH＝2x，则PE＝GC＝3x，HG＝5x，
∴BC＝2x＋5x＋3x＝10x，∵△PDF∽△CBA，∴ ，∴S△ABC＝25S△PDF＝25S1＝100.
教材母题2(人教九下39页习题2)如图，Rt△ABC中，CD是斜边AB上的高．求证：(1)△ACD ∽△ABC；(2)△CBD ∽△ABC.注：射影定理：Rt△ABC中，若CD为高，则有CD2＝BD·AD，BC2＝BD·AB或AC2＝AD·AB.
证明：(1)∵CD是斜边AB上的高，∴∠ADC＝∠BDC＝90°，∴∠ADC＝∠ACB＝90°，∵∠A＝∠A，∴△ACD ∽△ABC；(2)由(1)知，∠BDC＝∠ACB＝90°，又∵∠B＝∠B，∴△CBD ∽△ABC.
【还能这样考】1. 如图，在△ABC中，CD为AB边上的高，且AC2＝AD·AB.求证：(1)∠DCB＝∠A；(2)△ABC为直角三角形．
1. 证明：(1)∵AC2＝AD·AB，∴ ，∵∠A＝∠A，∴△ACD ∽△ABC，∴∠ACD＝∠B，∵CD为AB边上的高，∴∠ACD＋∠A＝90°，∠B＋∠DCB＝90°，∴∠DCB＝∠A；
2. 如图，在△ABC中，D为AB上一点，且∠ACD＝∠B，求证：AC2＝AD·AB.
(2)由(1)知∠B＋∠A＝90°，∴∠ACB＝90°，即△ABC为直角三角形．2. 证明：∵∠ACD＝∠B，∠A＝∠A，∴△ACD ∽△ABC，∴ ，∴AC2＝AD·AB.
3. 如图，在△ABC中，AD平分∠BAC，AD的垂直平分线交AB于点E，交AD于点H，交BC的延长线于点F，求证：DF2＝CF·BF.
3. 证明：如解图，连接AF，∵FH垂直平分AD，∴ FA＝FD，∠FAD＝∠FDA，∵ AD平分∠BAC，∴∠CAD＝∠BAD，∴∠FAD－∠CAD＝∠FDA－∠BAD，∵∠B＝∠FDA－∠BAD，