2022年中考数学二轮复习专题《图形的对称、平移、旋转》课件PPT

这是一份2022年中考数学二轮复习专题《图形的对称、平移、旋转》课件PPT，共41页。PPT课件主要包含了图形的对称，第4题图，第4题解图，图形的平移，第2题图，图形的旋转，旋转方向，旋转角，第1题图，位似图形的性质等内容，欢迎下载使用。

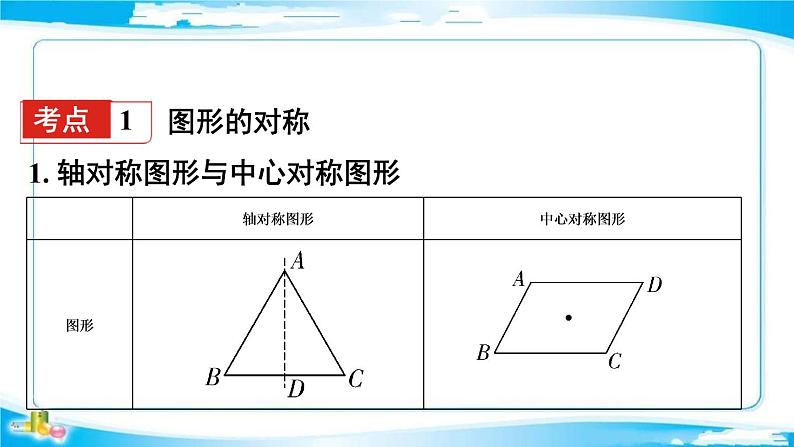
1. 轴对称图形与中心对称图形
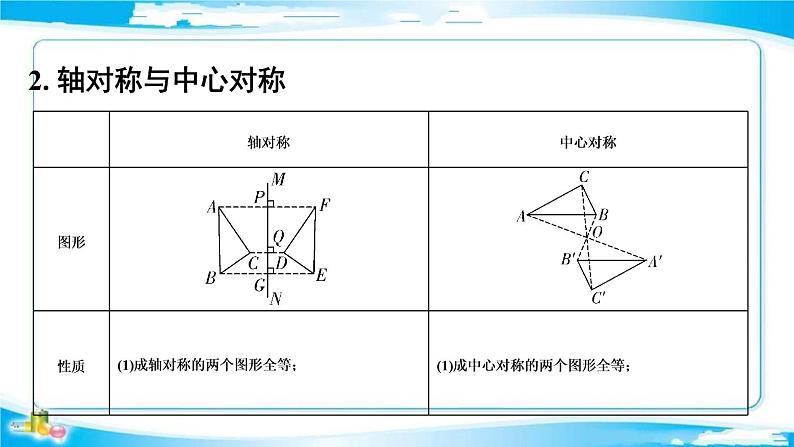
2. 轴对称与中心对称
1. 下列生态环保标志中，是中心对称图形的是(　　)
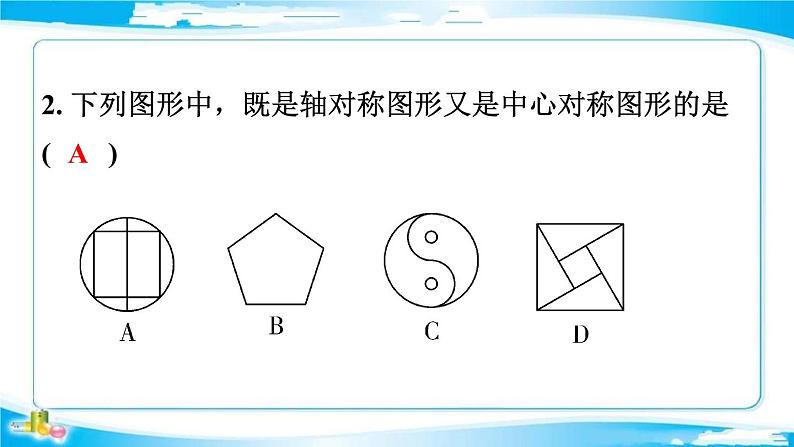
2. 下列图形中，既是轴对称图形又是中心对称图形的是(　　)
3. 以下图形，对称轴的数量小于3的是(　　)
4. 如图，正三角形网格中，已有两个小正三角形被涂灰，再将图中其余小正三角形涂灰一个，使整个被涂灰的图案构成一个轴对称图形的方法有________种．
【解析】如解图，将图中其余小正三角形涂灰一个，使整个被涂灰的图案构成一个轴对称图形的方法有3种．
1. 平移的三大要素：一是平移的①________，二是平移的②________，三是平移的距离．2. 平移的性质(1)平移前后，对应线段平行且相等，对应角③________；(2)对应点所连线段平行(或在同一条直线上)且相等；(3)平移是全等变换，即平移前后两图形④________．
已知△ABC顶点坐标分别是A(0，6)，B(－3，－3)，C(1，0)，将△ABC平移后顶点A的对应点A1的坐标是(4，10)，则点B的对应点B1的坐标为(　　)A. (7，1)　　　　　　B. (1，7)C. (1，1) D. (2，1)
【解析】将△ABC平移，使得点A(0，6)变成A1(4，10)，则三角形先向右平移4个单位长度，再向上平移4个单位长度，则点B先向右平移4个单位长度，再向上平移4个单位长度得到点B1，∵点B(－3，－3)，∴点B1(1，1)．
2.如图，将△ABE向右平移2 cm得到△DCF，如果△ABE的周长是16 cm，那么四边形ABFD的周长是_____ cm
1. 旋转的三大要素：旋转中心、⑤________和⑥________．2. 旋转的性质(1)对应点到旋转中心的距离相等；(2)对应点与旋转中心所连线段的夹角等于旋转角；(3)旋转前、后的图形全等．
【解析】∵∠CAC′是旋转角，∠CAB＝30°，∴∠CAC′＝180°－∠CAB＝150°，即三角板ABC旋转的度数为150°.
1. 如图，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的度数是(　　)A. 60° 　　 B. 90°　 　C. 120° 　　D. 150°
2. 如图，将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点，若∠CAE＝90°，AB＝1，则BD＝______
1. 位似图形上的任意一对对应点到位似中心的距离的比等于⑦______，面积比等于相似比的平方；2. 位似图形对应点的连线或延长线相交于同一点；3. 位似图形对应边平行(或在同一条直线上)；4. 位似图形对应角相等．【温馨提示】位似是相似的一种特殊情况，若两个三角形位似，则这两个三角形必定相似．
1. 如图，线段CD两个端点的坐标分别为C(1，2)、D(2，0)，以原点O为位似中心，将线段CD放大得到线段AB，若点B的坐标为(5，0)，则点A的坐标为(　　)
A. (2，5)　 　B. ( ，5) C. (3，5) D. (3，6)
2. 如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′.已知OB＝3OB′，则△A′B′C′与△ABC的面积比为(　　)A. 1∶3　　　 　B. 1∶4 C. 1∶8 D. 1∶9
【解析】∵OB＝3OB′，∴ ，∵以点O为位似中心，将△ABC缩小后得到△A′B′C′，∴△A′B′C′∽△ABC，∴ ，∴ .
1. 对称作图的基本步骤(1)找出原图形的关键点；(2)作出关键点关于对称轴(或对称中心)的对称点；(3)按原图形依次连接得到的各关键点的对应点，得到对称的图形．
2. 平移作图的基本步骤(1)根据题意，确定平移的方向和平移距离；(2)找出原图形的关键点；(3)按平移方向和平移距离，平移各个关键点，得到各关键点的对应点；(4)按原图形依次连接得到的各关键点的对应点，得到平移后的图形．
3. 旋转作图的基本步骤(1)根据题意，确定旋转中心及旋转方向、旋转角度；(2)找出原图形的关键点；(3)连接关键点与旋转中心，按旋转方向与旋转角度将它们旋转，得到各关键点的对应点；(4)按原图形依次连接得到的各关键点的对应点，得到旋转后的图形．
4. 位似作图的基本步骤(1)确定位似中心；(2)确定原图形的关键点；(3)确定位似比，即要将图形放大或缩小的倍数；(4)作出原图形中各个关键点的对应点；(5)按原图形的连接顺序连接所作的各个对应点．
1. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2，－1)，B(3，－3)，C(0，－4)．(1)画出△ABC关于原点O成中心对称的△A1B1C1；(2)画出△A1B1C1关于y轴对称的△A2B2C2.
解：(1)画出△A1B1C1如解图；(2)画出△A2B2C2如解图．
2. 已知：如图，△ABC三个顶点的坐标分别为A(0，－3)，B(3，－2)，C(2，－4)(正方形网格中，每个小正方形的边长是1个单位长度)．(1)画出△ABC向上平移6个单位得到的△A1B1C1；(2)以点C为位似中心，在网格中画出△A2B2C，使△A2B2C与△ABC位似，且△A2B2C与△ABC的位似比为2∶1，并直接写出点A2的坐标．
解：(1)画出△A1B1C1如解图；(2)画出△A2B2C如解图，点A2的坐标为(－2，－2)．
(人教八上85页)如图所示，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地．牧马人到河边的什么地方饮马，可使所走的路径最短？(将军饮马问题)
解：如解图所示，作点A关于直线l的对称点A′，连接A′B交l于点P，则牧马人到河边P处饮马，所走的路径最短．理由如下：可在l上任取一点P′，由轴对称的知识可得在P点所走的路程为A′B，在P′点时所走的路程为A′P′＋P′B，∵A′P′＋P′B′＞A′B，∴P为所求的点．
【还能这样考】1. (2015玉林防城港)如图，已知正方形ABCD边长为3，点E在AB边上且BE＝1，点P，Q分别是边BC，CD的动点(均不与顶点重合)，当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是________．
【解析】如解图，作点A关于DC的对称点M，作点E关于BC的对称点N，连接MN，分别交DC、BC于点Q、P，此时，四边形AEPQ的周长最小．在正方形ABCD中，∵DC∥AB，BC∥AD，∴△MDQ∽△MAN，△NPB∽△NMA，∴ ， ，∴DQ＝2，PB＝1.5， ∴S四边形AEPQ＝S△MAN － S△MAQ
－ S△PEN ＝ ×4×6－ ×6×2－ ×2×1.5＝4.5，∴当四边形AEPQ周长最小时，四边形AEPQ的面积是4.5.
2. 如图，在正方形ABCD中，AB＝2，P是对角线AC上任意一点，若M是BC边上的中点，求PM＋PB的最小值．
解：∵四边形ABCD是正方形，∴作B点关于AC的对称点即为点D.如解图，连接DM，DM与AC的交点为P，此时PM＋PB的值最小，∵BC＝CD＝AB＝2，M是BC的中点，∴CM＝1，∴PM＋PB＝PM＋PD＝DM＝ ，∴PM＋PB的最小值为.
3. 如图，在正方形ABCD中，AB＝2，E是AB的中点，P是EC上任意一点，M是BC边上任意一点，求PB＋PM的最小值．
解：如解图，作点B关于CE的对称点B′，连接BB′，交CE于点F，过点B′作B′M⊥BC于点M，交CE于点P，此时PB＋PM最小．∵BB′⊥CE，∴∠FBC＋∠ECB＝90°，又∵B′M⊥BC，∴∠BMB′＝∠CBE＝90°，∠FBC＋∠BB′M＝90°
∴∠BB′M＝∠ECB，∴△BB′M∽△ECB，∴ ，∵AB＝2，E是AB的中点，∴BC＝2，BE＝ AB＝1，∴CE＝ ，∵BC·BE＝CE·BF，