






数学语文版(中职)第五单元 三角函数5.6 诱导公式授课ppt课件
展开同角三角函数的基本关系
1.任意角α的正弦、余弦、正切是怎样定义的?
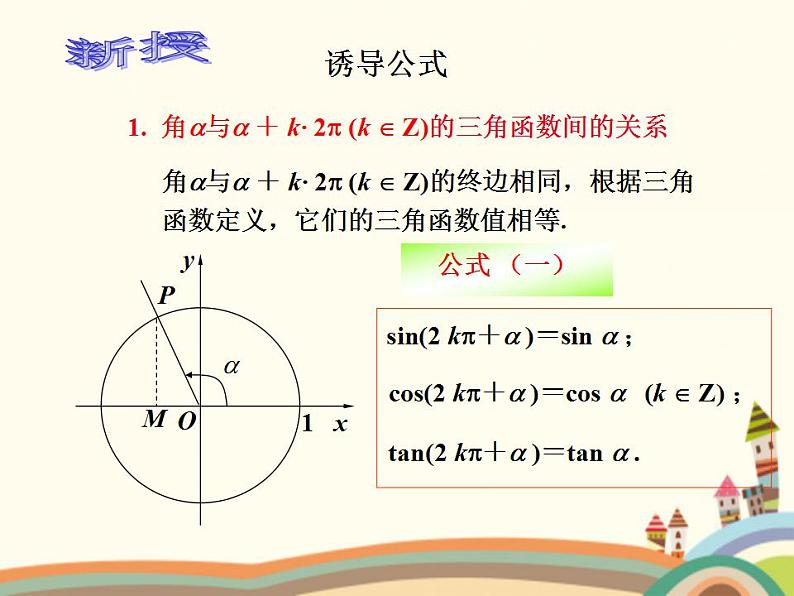
1. 角与 + k· 2 (k Z)的三角函数间的关系
角与 + k· 2 (k Z)的终边相同,根据三角函数定义,它们的三角函数值相等.
例1 求下列各三角函数的值:
探究 若 与 - 的终边关于 x 轴对称, 它们的三角函数之间有什么关系?
P (cs ,sin )
P (cs (-) ,sin(- ) )
2. 角 与 - 的三角函数间的关系
例 2 求下列各三角函数的值:
探究 若 与 - 的终边关于y轴对称, 它们的三角函数之间有什么关系?
3. 角 与 - 的三角函数间的关系
探究 2 若 与 + 的终边关于原点对称, 它们的三角函数之间有什么关系?
4. 角 与 + 的三角函数间的关系
例 求下列各三角函数的值:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,再放上将α当作锐角时原函数值的符号.
例 1 求下列各角的三角函数值。
由诱导公式可将任意的三角函数化为锐角三角函数,一般步骤如下:
(1)化负角的三角函数为正角的三角函数。
(3)化为锐角的三角函数。
概括为:“负化正,正化小,化到锐角就终了。”
语文版(中职)基础模块上册4.5 对数图片ppt课件: 这是一份语文版(中职)基础模块上册4.5 对数图片ppt课件,共19页。
语文版(中职)基础模块上册第四单元 指数函数与对数函数4.5 对数评课课件ppt: 这是一份语文版(中职)基础模块上册第四单元 指数函数与对数函数4.5 对数评课课件ppt,共16页。PPT课件主要包含了1积的对数,2商的对数,3幂的对数,完成书本108页练习,对数的运算法则,补充公式等内容,欢迎下载使用。
语文版(中职)基础模块上册第四单元 指数函数与对数函数4.5 对数多媒体教学课件ppt: 这是一份语文版(中职)基础模块上册第四单元 指数函数与对数函数4.5 对数多媒体教学课件ppt,共14页。PPT课件主要包含了本课要点,对数定义,对数运算性质,典型例题,对数函数图像与性质,细胞分裂问题,我们知道,对数的定义,指数式和对数式的互化等内容,欢迎下载使用。












