还剩27页未读，
继续阅读
所属成套资源：语文版-中职数学基础模块上册同步课件PPT
成套系列资料，整套一键下载
语文版（中职）基础模块上册4.6 对数函数的图像与性质教案配套ppt课件
展开
这是一份语文版（中职）基础模块上册4.6 对数函数的图像与性质教案配套ppt课件，共35页。PPT课件主要包含了对数函数及其性质，对数函数，小试牛刀，对数图像的作法，探索研究，求下列函数的定义域，-4，习题讲解，定义域为，你能口答吗等内容，欢迎下载使用。
判断：以下函数是对数函数的是 （ ）A. y=lg2(3x-2) B. y=lg(x-1)xC. y=lg1/3x2 D.y=lnxE.
（1）{x|x≠0}（2）{x|x<4} (3){x|x>1} (4){x|x>0且x≠1}
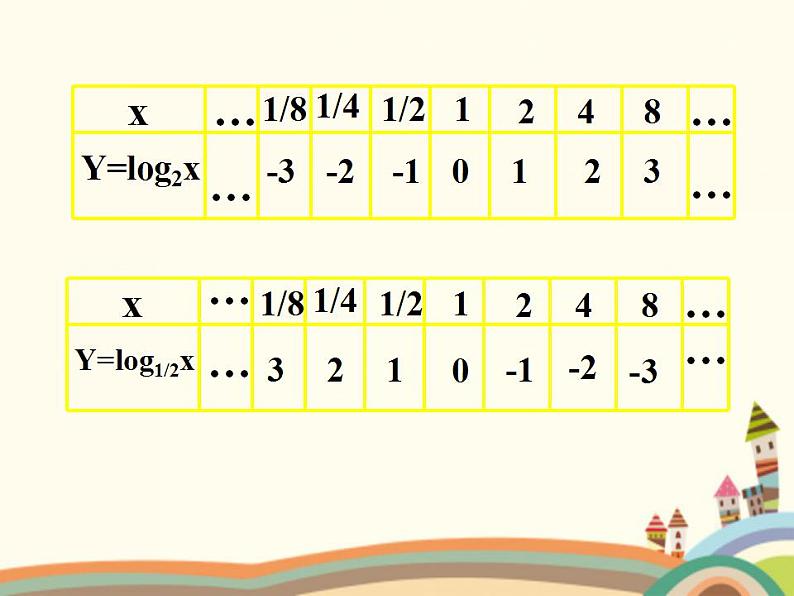
作对数图像的三个步骤：一、列表（根据给定的自变量分别计算出应变量的值）二、描点（根据列表中的坐标分别在坐标系中标出其对应点）三、连线（将所描的点用平滑的曲线连接起来）
y=lg x 和y=lg x 作图
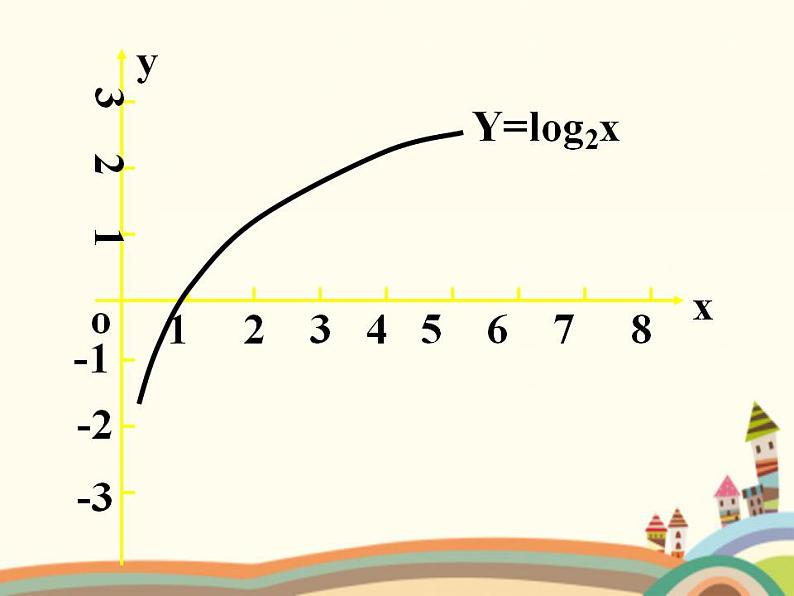
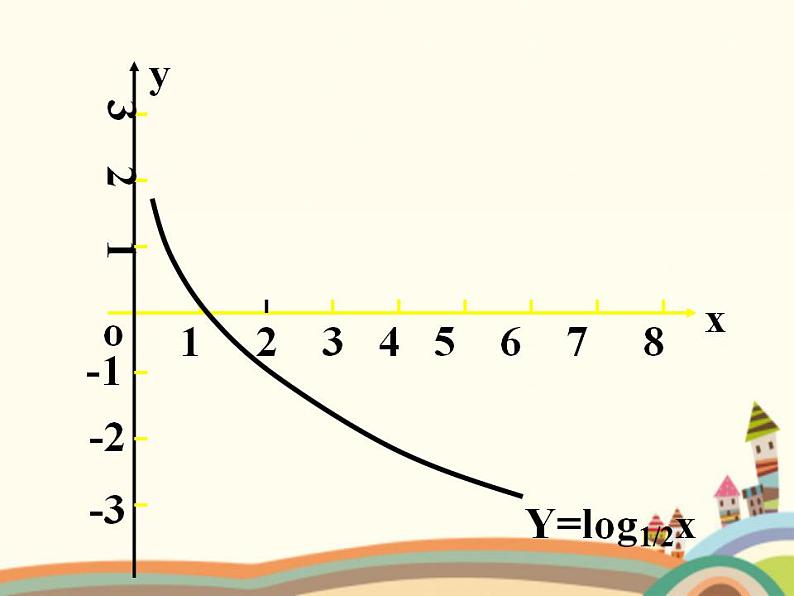
y = Lg2 x与y = Lg 0.5 x的图像分析
因为指数函数y=ax (0
( 0 , + ∞ )
( 1 , 0 ) 即 x = 1 时，y = 0
在 ( 0 , + ∞ ) 上是增函数
在 ( 0 , + ∞ ) 上是减函数
当 x＞1 时，y＞0当 0＜x ＜1 时， y＜0
当 x＞1 时，y＜0当 0＜x＜1 时，y＞0
底数互为倒数的两个对数函数的图象关于x轴对称。
0
指数函数、对数函数性质比较一览表
(1) y=lgax2 (2) y=lga(4-x)
(1)因为x2>0,所以x≠,即函数y=lgax2的定义域为
- (0,+
(2)因为 4-x>0,所以x<4,即函数y=lga(4-x)的定义域为
(3) y=lg(x-1)(3-x) (4) y=lg0.5(4x-3)
(3) 3-x>0 因为 x-1>0 x-1≠
所以 1
(4)因为 4x-3>0 lg0.5(4x-3)0
x>3/44x-3≤
比较下列各组中，两个值的大小：（1） lg23.4与 lg28.5 （2） lg 0.3 1.8与 lg 0.3 2.7
比较两个同底对数值的大小时:
１.观察底数是大于1还是小于1（ a>1时为增函数 0
３.根据单调性得出结果。
注意：若底数不确定，那就要对底数进行分类讨论即0 1
比较下列各组中，两个值的大小：（3） lga5.1与 lga5.9
解: ①若a>1则函数在区间（0，+∞）上是增函数； ∵5.1<5.9 ∴ lga5.1 < lga5.9
②若0 lga5.9
比较下列各组中两个值的大小: ⑴ lg 67 , lg 7 6 ; ⑵ lg 3π , lg 2 0.8 .
注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小
㈠ 若底数为同一常数,则可由对数函数的单调性直接进行判断.㈡ 若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.㈢ 若底数、真数都不相同,则常借助1、0、－1等中间量进行比较
比较两个对数值的大小.
比较a、b、c、d、1的大小。
答：b>a>1>d>c
（1）本节要求掌握对数函数的概念、图象和性质．（2）在理解对数函数的定义的基础上，掌握对数函数的图象和性质的应用是本小节的重点．
题型一.求函数的定义域.
速度训练:求下列函数的定义域
变式:将2换成1/2呢?
例2：求函数 y=lg3x(1≤x≤3)的值域.
拓展:指出下列函数的值域
题型三： 解下列关于x的不等式:
解不等式lgax>lga(1-x)（ａ＞０且ａ≠１) 时，你首先想到要做什么？
(1) lg0.5x > lg0.5(1-x)
(2) lg2(x+3) < 0
题型四. 求单调区间：
依据：复合函数的单调性的判定方法.
(注意：要考虑函数的定义域)
例4.函数ｙ＝lg2(x2- 3x+2) 的单调减区间 是________
判断：以下函数是对数函数的是 （ ）A. y=lg2(3x-2) B. y=lg(x-1)xC. y=lg1/3x2 D.y=lnxE.
（1）{x|x≠0}（2）{x|x<4} (3){x|x>1} (4){x|x>0且x≠1}
作对数图像的三个步骤：一、列表（根据给定的自变量分别计算出应变量的值）二、描点（根据列表中的坐标分别在坐标系中标出其对应点）三、连线（将所描的点用平滑的曲线连接起来）
y=lg x 和y=lg x 作图
y = Lg2 x与y = Lg 0.5 x的图像分析
因为指数函数y=ax (0
( 0 , + ∞ )
( 1 , 0 ) 即 x = 1 时，y = 0
在 ( 0 , + ∞ ) 上是增函数
在 ( 0 , + ∞ ) 上是减函数
当 x＞1 时，y＞0当 0＜x ＜1 时， y＜0
当 x＞1 时，y＜0当 0＜x＜1 时，y＞0
底数互为倒数的两个对数函数的图象关于x轴对称。
0
指数函数、对数函数性质比较一览表
(1) y=lgax2 (2) y=lga(4-x)
(1)因为x2>0,所以x≠,即函数y=lgax2的定义域为
- (0,+
(2)因为 4-x>0,所以x<4,即函数y=lga(4-x)的定义域为
(3) y=lg(x-1)(3-x) (4) y=lg0.5(4x-3)
(3) 3-x>0 因为 x-1>0 x-1≠
所以 1
(4)因为 4x-3>0 lg0.5(4x-3)0
x>3/44x-3≤
比较下列各组中，两个值的大小：（1） lg23.4与 lg28.5 （2） lg 0.3 1.8与 lg 0.3 2.7
比较两个同底对数值的大小时:
１.观察底数是大于1还是小于1（ a>1时为增函数 0
３.根据单调性得出结果。
注意：若底数不确定，那就要对底数进行分类讨论即0
比较下列各组中，两个值的大小：（3） lga5.1与 lga5.9
解: ①若a>1则函数在区间（0，+∞）上是增函数； ∵5.1<5.9 ∴ lga5.1 < lga5.9
②若0
比较下列各组中两个值的大小: ⑴ lg 67 , lg 7 6 ; ⑵ lg 3π , lg 2 0.8 .
注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小
㈠ 若底数为同一常数,则可由对数函数的单调性直接进行判断.㈡ 若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.㈢ 若底数、真数都不相同,则常借助1、0、－1等中间量进行比较
比较两个对数值的大小.
比较a、b、c、d、1的大小。
答：b>a>1>d>c
（1）本节要求掌握对数函数的概念、图象和性质．（2）在理解对数函数的定义的基础上，掌握对数函数的图象和性质的应用是本小节的重点．
题型一.求函数的定义域.
速度训练:求下列函数的定义域
变式:将2换成1/2呢?
例2：求函数 y=lg3x(1≤x≤3)的值域.
拓展:指出下列函数的值域
题型三： 解下列关于x的不等式:
解不等式lgax>lga(1-x)（ａ＞０且ａ≠１) 时，你首先想到要做什么？
(1) lg0.5x > lg0.5(1-x)
(2) lg2(x+3) < 0
题型四. 求单调区间：
依据：复合函数的单调性的判定方法.
(注意：要考虑函数的定义域)
例4.函数ｙ＝lg2(x2- 3x+2) 的单调减区间 是________
相关课件
语文版（中职）基础模块上册第五单元 三角函数5.8 余弦函数的图像和性质示范课ppt课件： 这是一份语文版（中职）基础模块上册第五单元 三角函数5.8 余弦函数的图像和性质示范课ppt课件，共27页。PPT课件主要包含了余弦函数的图象，余弦曲线，正弦曲线，与x轴的交点，图象的最高点，图象的最低点，五点作图法，简图作法，正弦函数的图象，值域-11等内容，欢迎下载使用。
数学5.8 余弦函数的图像和性质教课课件ppt： 这是一份数学5.8 余弦函数的图像和性质教课课件ppt，共27页。PPT课件主要包含了余弦函数的图象，余弦曲线，正弦曲线，与x轴的交点，图象的最高点，图象的最低点，五点作图法，简图作法，正弦函数的图象，值域-11等内容，欢迎下载使用。
语文版（中职）基础模块上册4.6 对数函数的图像与性质课文课件ppt： 这是一份语文版（中职）基础模块上册4.6 对数函数的图像与性质课文课件ppt，共23页。PPT课件主要包含了目标与要求，〔学习要求〕，准备导入，探究与深化，〔探究与深化一〕，〔探究与深化二〕，〔探究与深化三〕，图像过定点10，练习与评价，〔练习与评价一〕等内容，欢迎下载使用。
