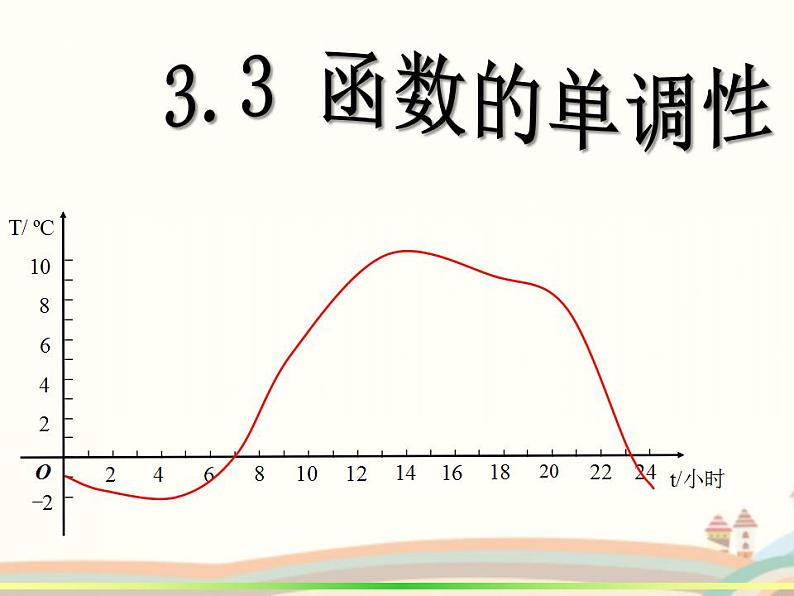
数学基础模块上册第三单元函数3.3 函数的单调性课文ppt课件

展开

这是一份数学基础模块上册第三单元函数3.3 函数的单调性课文ppt课件，共20页。PPT课件主要包含了3函数单调性，收入万元，人数人，-∞0，0+∞，y＝x＋1，y＝－2x＋2，y＝－x2＋2x，课本54页练习3-3等内容，欢迎下载使用。

3.3函数单调性
学习目标：1.理解增函数、减函数的定义。2.能根据函数图像说出函数是增函数还是减函数。3.学会根据函数图像找出函数的单调区间
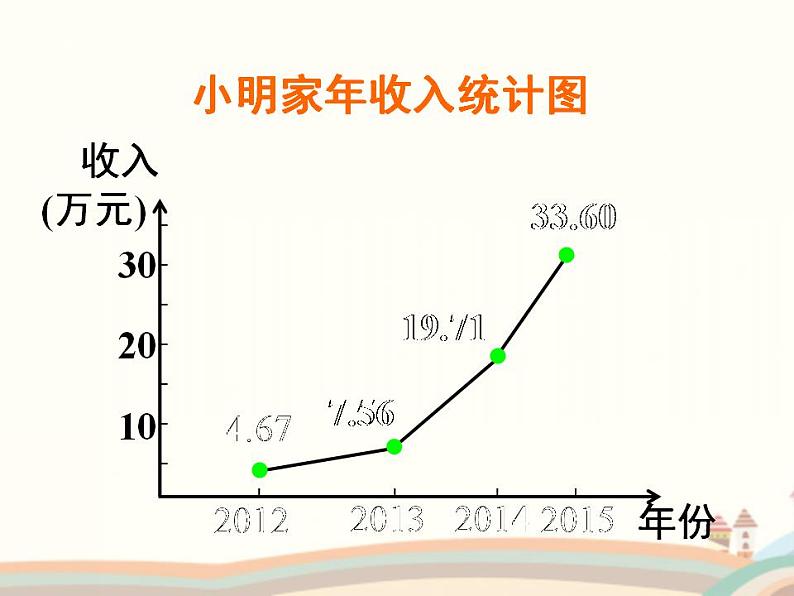
小明家年收入统计图
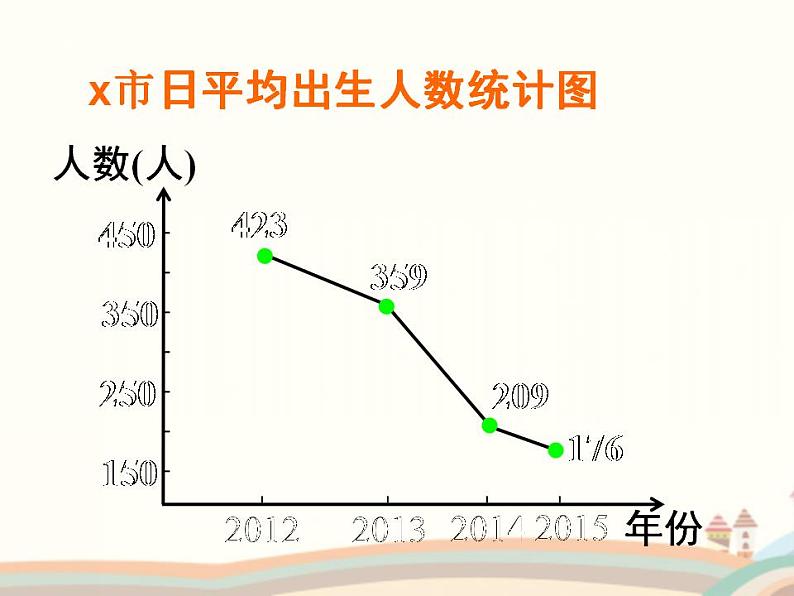
x市日平均出生人数统计图
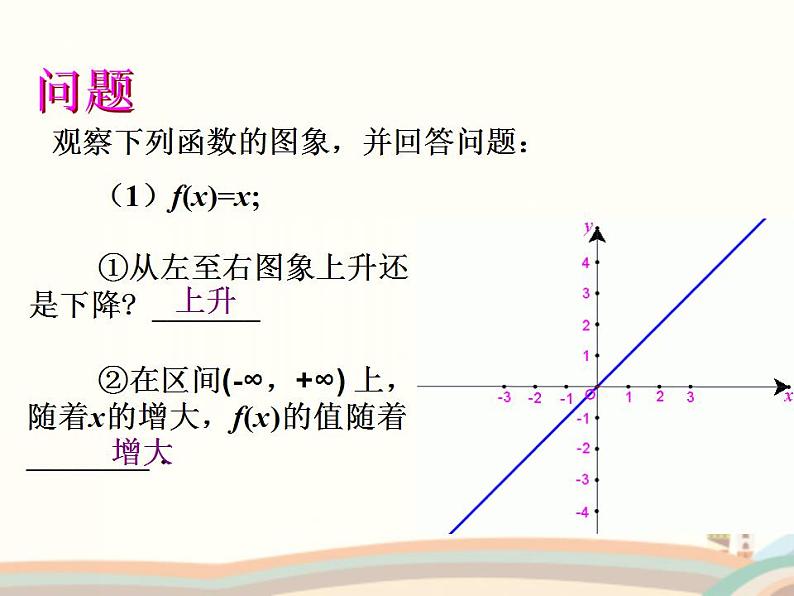
观察下列函数的图象，并回答问题：
（1）f(x)=x;
①从左至右图象上升还是下降? _______
②在区间(-∞，+∞) 上，随着x的增大，f(x)的值随着 ________ ．
(2) f（x）=-x： ①从左至右图象上升还是下降 ___ ? ②在区间(-∞,+∞)上，随着x的增大， f（x）值随着 ______ ．
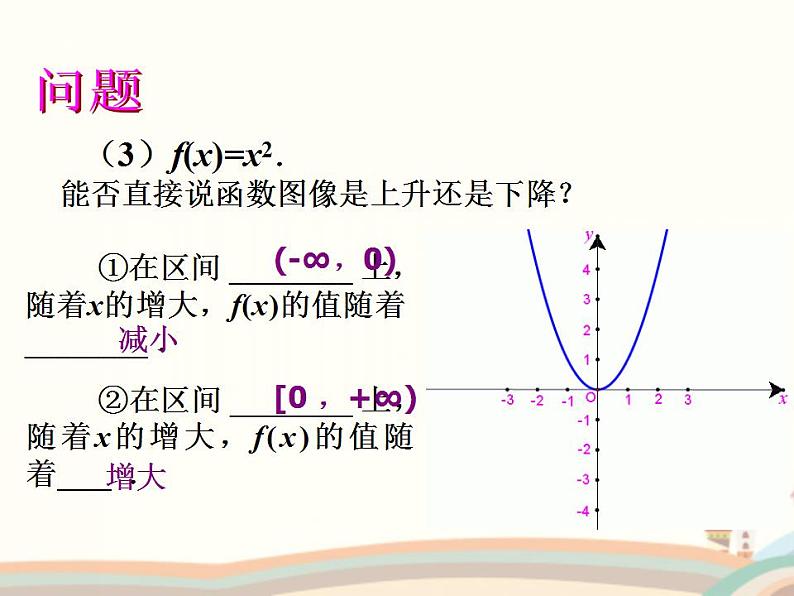
（3）f(x)=x2．能否直接说函数图像是上升还是下降？
①在区间 ________ 上，随着x的增大，f(x)的值随着 ________ ．
②在区间 ________ 上，随着x的增大，f(x)的值随着．
看课本52页，回答问题。
1、什么叫做增函数，什么叫做减函数？2、根据增函数、减函数的定义，说出由函数解析式判断函数是增函数或减函数的一般步骤。3、什么叫做函数的单调性，函数的单调区间？
从上面的图像可以看出：不同的函数，其图象的变化趋势不同，同一函数在不同区间上变化趋势也不同，函数图象的这种增、减变化就是函数的一个重要性质——函数的单调性．
为了刻画函数的这种增、减性质我们引入增函数和减函数。
f(x)=x的图象;
从左至右是上升的，即在区间(-∞,+∞)上，随着x的增大，f(x)的值随着增大，这样的函数我们称为增函数。
f（x）=-x的图像：从左至右是下降的，即在区间 (-∞,+∞) 上，随着x的增大， f（x）值随着减小，这样的函数称为减函数．
如何用f（x）与x解析式定义增函数和减函数：对于给定区间上的函数y=f（x）
在y=f(x)的图像上任取两点A(x1, y1), B(x2, y2)，记△x=x2-x1，△y= f(x2)- f(x1)= y2- y1
议一议：观察下列函数f(x)=x2的图象，说出它是增函数还是减函数：
①在区间(-∞，0)上，随着x的增大，f(x)的值随之减小．所以在区间(-∞，0)上是——
②在区间[0 ，+∞)上，随着x的增大，f(x)的值随着增大．所以在区间[0 ，+∞)上是————
说一说：说出以下函数是增函数还是减函数？
例1：如图，函数y=f（x）的定义域是[-10，10]，根据图象指出函数y=f（x）的单调区间，并指出每一个单调区间上函数y=f（x）的单调性
解：函数y=f（x）的单调区间有[-10，-4)，[-4,-1)，[-1,2)，[2,8），[8，10] 其中函数y=f（x）在区间[-10，-4)， [-1,2)，[8，10]上是减函数在区间[-4,-1)， [2,8）上是增函数。
例2：证明函数f（x）=2x+1在（-∞，+∞）上是增函数。
证明：设x1，x2是任意两个不相等的实数。因为Δx=x2-x1，而且Δy= f（x2）- f（x1） =（2x2+1）-（2x1+1） =2（x2-x1） =2Δx所以 =2 Δx/ Δx=2 ＞0因此函数f（x）=2x+1在（ -∞，+∞）上是增函数。
例3:证明函数 f (x) = 在区间(-∞，0)上是减函数．
证明：设 x1，x2 是任意两个不相等的负实数，因为Δx=x2-x1，而且Δy= f（x2）- f（x1）又因为x1x2 ＞0，所以因此 f (x) = 在区间(0 ，＋∞)上是减函数．