高中数学语文版（中职）基础模块上册2.1 不等式的基本性质课堂教学ppt课件

这是一份高中数学语文版（中职）基础模块上册2.1 不等式的基本性质课堂教学ppt课件，共11页。PPT课件主要包含了a-c等内容，欢迎下载使用。

【一】、回顾过去 展望未来
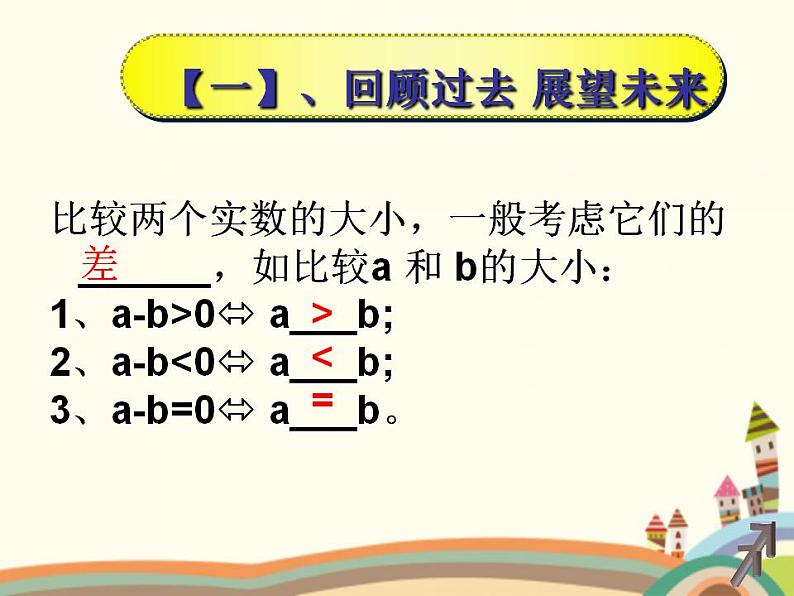
比较两个实数的大小，一般考虑它们的______，如比较a 和 b的大小：1、a-b>0 a___b; 2、a-b<0 a___b; 3、a-b=0 a___b。
二、探索新知 汇报展示
性质1 不等式的传递性: 如果a>b，且b>c，那么a___c．证明: 由a>b => a-b___0 由b>c => b-c___0 所以(a-b)+(b-c)___0 （两个大于0的式子相 加，其结 果____0） 化简得：________ > 0 因此:a >c
观察3>2，可知3+1>2+1
性质2 不等式的加法性质：如果a>b，那么 a+c___b+c． 语言描述：不等式的两边同时加（或减）同一个数，不等号的方向不变.（提示：“减”一个数相当于加这个数的相反数） 证明: 由a>b => a-b___0 (a+c)-(b+c)=a-b____0 因此a+c____b+c
观察3>1,可知2×3>2×1, -2×3<-2×1。
性质3 不等式的乘法性质：（1）如果a>b,c>0,那么ac____bc;（2）如果a>b,c<0,那么ac____bc.语言描述：不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变; 不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变。（提示：“除以”一个数相当于“乘以”这个数的倒数）证明 (1) (2)
性质3 不等式的乘法性质：（1）如果a>b,c>0,那么ac____bc;（2）如果a>b,c<0,那么ac____bc.证明：（1） 由a>b 所以a-b___0 又已知：c>0 所以： ac-bc=c(a-b)___0 [已得：c>0,(a-b)>0] 因此：ac>bc(2) 由a>b 所以 a-b___0 又已知：c<0 所以： ac-bc=c(a-b)___0 [已得：c<0,(a-b)>0] 因此：ac 三、巩固知识 典型例题
例1：用符号“>”或“<”填空，并说出应用了不等式的哪条性质．(1)如果3x+2>-1,那么3x____-3;(2) 如果3x<6, 那么x___2;(3) 如果-5x>10, 那么x____-2;(4) 如果a>b>0, 那么3a___3b,3b____2b,3a_____2b.
解:（1）3x>-3, 运用了不等式性质1. （2）x<2 ，运用了不等式性质2. (3)x<-2，运用了不等式性质3. (4)3a>3b, 运用了不等式性质2. 3b>2b, 运用了不等式性质2. 3a>2b，运用了不等式性质4.
四、运用知识 强化练习
随堂练习：1.判断下列命题是否正确，并说明理由。
五、归纳小结 强化思想
1、本次课学了哪些内容
2、自己如何进行学习的