








2020-2021学年3.1 函数集体备课课件ppt
展开1. 请举几个学过的函数的例子.
2. 初中函数定义: 在一个变化过程中,有两个变量 x 和 y,如果给定一个 x 值,就相应地确定了唯一的 y 值,那么我们就称 y 是 x 的函数,其中x是自变量,y 是因变量.
正比例函数:y = kx (k 0) 一次函数: y = kx+b (k 0) 二次函数: y = ax2+bx+c (a 0)
一辆汽车在一段平坦的道路上以100 km/h的速度匀速行驶 2 小时.
(1) 在这个问题中,路程、时间、速度这三个量,哪些是常量?哪些是变量?
(2) 如何用数学式子表示行驶的路程 s (km)与行驶时间 t (h)之间的关系?
(3) 行驶时间 t (h)的取值范围是什么?
(4) 对于行驶时间中的每一个确定的 t 值,你能求出汽车行驶的路程吗?
(5) 根据初中知识,关系式 s = 100t (0 ≤t ≤2)表示的是函数关系吗?
如果一个圆的半径用 r 表示,它的面积用 A 表示.
(1) 你能用数学式子表示圆的面积 A 与它的半径 r 之间的关系吗?
(2) 在 A 与 r 的关系式中,r 的取值范围是什么?
(3) 关系式 A = r2(r>0)表达的是一种函数关系吗?因变量是哪个量?自变量是哪个量?
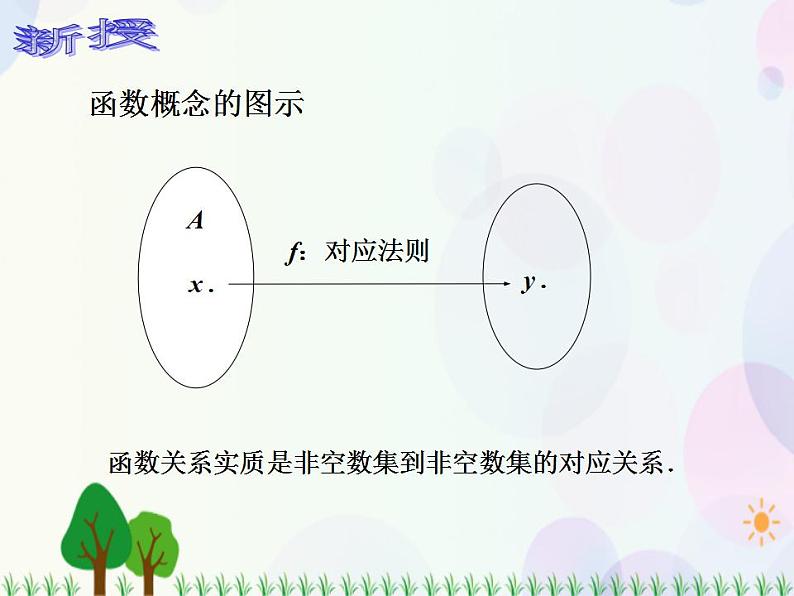
函数概念 设集合 A 是一个非空的实数集,对 A 内任意实数 x,按照某个确定的法则 f,有唯一确定的实数值 y 与它对应,则称这种对应关系为集合 A 上的一个函数.记作y= f (x).其中 x 为自变量,y 为因变量.自变量 x 的取值集合 A 叫做函数的定义域.对应的因变量 y 的取值集合叫做函数的值域.
集合 A 是一个非空的实数集
对应的因变量 y 的取值集合
函数关系实质是非空数集到非空数集的对应关系.
函数概念 设集合 A 是一个非空的实数集,对 A 内任意实数 x,按照某个确定的法则 f,有唯一确定的实数值 y 与它对应,则称这种对应关系为集合 A 上的一个函数.记作 y = f (x).其中 x 为自变量,y 为因变量.自变量 x 的取值集合 A 叫做函数的定义域.对应的因变量 y 的取值集合叫做函数的值域.
定义域和对应法则.
检验两个变量之间关系是否为函数的标准: (1)定义域是否给出; (2)对应法则是否给出,并且根据这个对应法则, 能否由自变量 x 的每一个值,确定唯一的 y 值.
例1 判断下列图中对应关系是不是函数:
函数概念 设集合 A 是一个非空的实数集,对 A 内任意实数 x,按照某个确定的法则 f,都有唯一确定的实数值 y 与它对应,则称这种对应关系为集合 A 上的一个数.记作 y = f (x).其中 x 为自变量,y 为因变量.自变量 x 的取值集合 A 叫做函数的定义域.对应的因变量 y 的取值集合叫做函数的值域.
函数的符号: 函数 y = f (x) 也经常写作函数 f (x) 或函数 f ;(2) 也可以将 y 是 x 的函数记为 y = g(x) 或者 y = h(x) 等;(3) 函数 y = f (x)在 x = a 处对应的函数值y,记作 y = f (a).
巩固练习:教材 P62,练习A 组第 2 题.
定义域:如果不特别指明,函数的定义域是使函数有意义的全体实数构成的集合.
函数概念 设集合 A 是一个非空的实数集,对 A 内任意实数 x,按照某个确定的法则 f,都有唯一确定的实数值 y 与它对应,则称这种对应关系为集合 A 上的一个函数.记作 y = f (x).其中 x 为自变量,y 为因变量.自变量 x 的取值集合 A 叫做函数的定义域.对应的因变量 y 的取值集合叫做函数的值域.
巩固练习:教材 P46 练习 第 5 题.
解:要使已知函数有意义,当且仅当
所以函数的定义域为{x|x≥-3,x≠0}.
数学基础模块上册(2021)3.1 函数的概念课文内容ppt课件: 这是一份数学基础模块上册(2021)3.1 函数的概念课文内容ppt课件,文件包含31函数的概念课件pptx、31函数的概念教案pdf等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
高中数学高教版(中职)基础模块上册(2021)3.1 函数的概念多媒体教学课件ppt: 这是一份高中数学高教版(中职)基础模块上册(2021)3.1 函数的概念多媒体教学课件ppt,共17页。PPT课件主要包含了学习目标,温馨提示,探究与发现,课堂小结等内容,欢迎下载使用。
高中数学第3章 函数3.1 函数的概念优质课课件ppt: 这是一份高中数学第3章 函数3.1 函数的概念优质课课件ppt,共16页。PPT课件主要包含了情境导入,探索新知,例题辨析,巩固练习,归纳总结,布置作业等内容,欢迎下载使用。












