

高中数学人教版新课标A必修2第二章 点、直线、平面之间的位置关系综合与测试测试题
展开第二章 学业质量标准检测
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线l1∥l2,在l1上取3个点,在l2上取2个点,由这5个点能确定平面的个数为( D )
A.5 B.4
C.9 D.1
[解析] 由经过两条平行直线有且只有一个平面可知分别在两平行直线上的5个点只能确定一个平面.
2.教室内有一直尺,无论怎样放置,在地面总有这样的直线,使得它与直尺所在直线( B )
A.平行 B.垂直
C.相交 D.异面
[解析] 当直尺垂直于地面时,A不对;当直尺平行于地面时,C不对;当直尺位于地面上时,D不对.
3.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( D )
A.若α,β垂直于同一平面,则α与β平行
B.若m,n平行于同一平面,则m与n平行
C.若α,β不平行,则在α内不存在与β平行的直线
D.若m,n不平行,则m与n不可能垂直于同一平面
[解析] A项,α,β可能相交,故错误;
B项,直线m,n的位置关系不确定,可能相交,平行或异面,故错误;
C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;
D项,假设m,n垂直于同一平面,则必有m∥n,所以原命题正确,故D项正确.
4.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( B )
A.相交 B.平行
C.异面 D.不确定
[解析] l∥m
5.已知α,β是两个平面,直线l⊄α,l⊄β,若以①l⊥α;②l∥β;③α⊥β中两个为条件,另一个为结论构成三个命题,则其中正确的命题有( A )
A.①③⇒②;①②⇒③
B.①③⇒②;②③⇒①
C.①②⇒③;②③⇒①
D.①③⇒②;①②⇒③;②③⇒①
[解析] 因为α⊥β,所以在β内找到一条直线m,使m⊥α
又因为l⊥α,所以l∥m.又因为l⊄β,所以l∥β,即①③⇒②;
因为l∥β,所以过l可作一平面γ∩β=n,所以l∥n
又因为l⊥α,所以n⊥α
又因为n⊂β,所以α⊥β,即①②⇒③.
6.设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有( B )
A.1条 B.2条
C.3条 D.4条
[解析] 如图,和α成30°角的直线一定是以A为顶点的圆锥的母线所在直线,当∠ABC=∠ACB=30°且BC∥l时,直线AC,AB都满足条件,故选B.
7.已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( C )
A.m∥l B.m∥n
C.n⊥l D.m⊥n
[解析] 选项A,只有当m∥β或m⊂β时,m∥l;选项B,只有当m⊥β时,m∥n;选项C,由于l⊂β,∴n⊥l;选项D,只有当m∥β或m⊂β时,m⊥n,故选C.
8.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,则异面直线AC与MN所成的角为( C )
A.30° B.45°
C.60° D.90°
[解析] 如图,连接A1C1,BC1,A1B.
∵M,N分别为棱BC和棱CC1的中点,
∴MN∥BC1.
又A1C1∥AC,
∴∠A1C1B为异面直线AC与MN所成的角.
∵△A1BC1为正三角形,
∴∠A1C1B=60°.故选C.
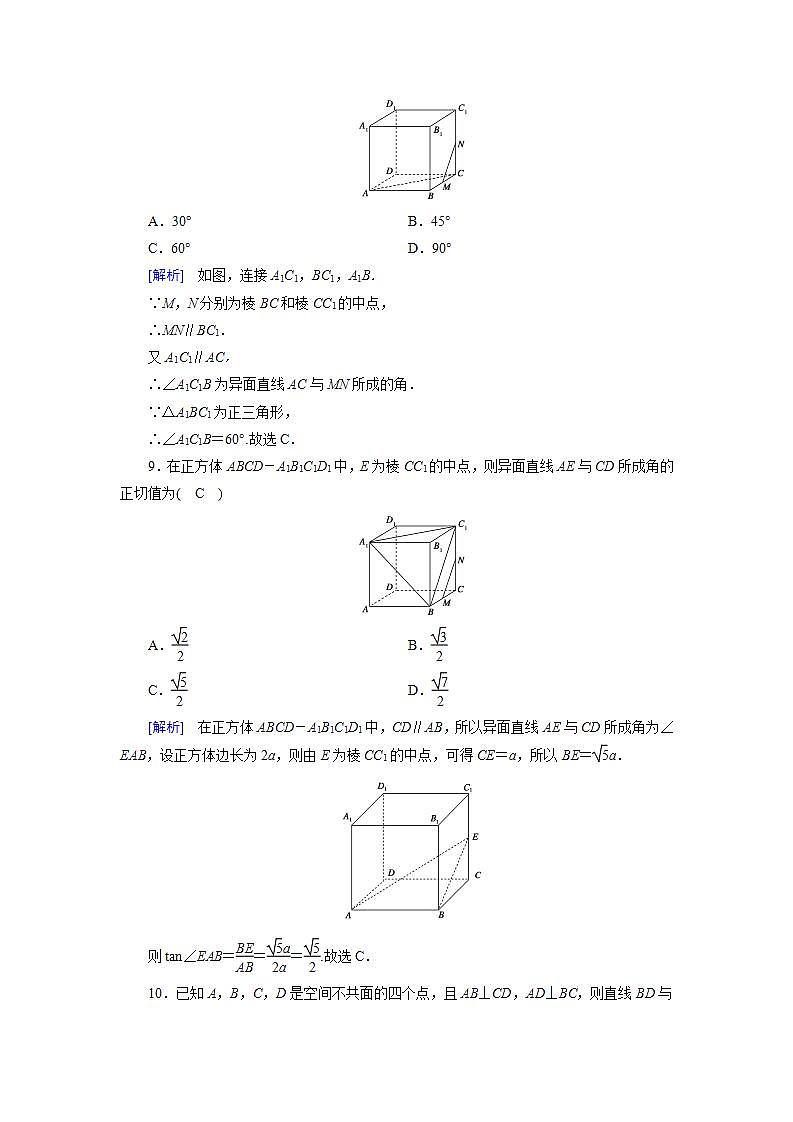
9.在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( C )
A. B.
C. D.
[解析] 在正方体ABCD-A1B1C1D1中,CD∥AB,所以异面直线AE与CD所成角为∠EAB,设正方体边长为2a,则由E为棱CC1的中点,可得CE=a,所以BE=a.
则tan∠EAB===.故选C.
10.已知A,B,C,D是空间不共面的四个点,且AB⊥CD,AD⊥BC,则直线BD与AC( A )
A.垂直 B.平行
C.相交 D.位置关系不确定
[解析] 过点A作AO⊥平面BCD,垂足为O,连结BO
∵AB⊥CD,由三垂线定理可得BO⊥CD.
同理DO⊥BC,∴O为△ABC的垂心
所以CO⊥BD,BD⊥AO,CO∩AO=O,∴BD⊥平面ADC,所以BD⊥AC.
故选A.
11.设a,b是异面直线,则以下四个结论:①存在分别经过直线a和b的两个互相垂直的平面;②存在分别经过直线a和b的两个平行平面;③经过直线a有且只有一个平面垂直于直线b;④经过直线a有且只有一个平面平行于直线b,其中正确的个数有( C )
A.1 B.2
C.3 D.4
[解析] 对于①,可对在两个互相垂直的平面中,分别画一条直线,当这两条直线异面时,可判断①正确;对于②,可在两个平行平面中,分别画一条直线,当这两条直线异面时,可判断②正确;对于③,当这两条直线不垂直时,不存在这样的平面满足题意,可判断③错误;对于④,假设过直线a有两个平面α,β与直线b平行,则面α,β相交于直线a,过直线b做一平面γ与面α,β相交于两条直线m,n都与直线b平行,可得a与b平行,所以假设不成立,所以④正确,故选C.
12. 已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( A )
A. B.
C. D.
[解析] 根据相互平行的直线与平面所成的角是相等的,所以在正方体ABCD-A1B1C1D1中,平面AB1D1与线AA1,A1B1,A1D1所成的角是相等的,
所以平面AB1D1与正方体的每条棱所在的直线所成角都是相等的,
同理平面C1BD也满足与正方体的每条棱所在的直线所成角都是相等的,
要求截面面积最大,则截面的位置为夹在两个面AB1D1与C1BD中间,
且过棱的中点的正六边形,且边长为,所以其面积为S=6×·()2=,故选A.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是__直角三角形__.
[解析] 如图,过点A作AE⊥BD,E为垂足.
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
∴AE⊥平面BCD,∴AE⊥BC.
又∵DA⊥平面ABC,∴DA⊥BC.
又∵AE∩DA=A,∴BC⊥平面ABD,
∴BC⊥AB.
∴△ABC为直角三角形.
14.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是棱AA1和AB上的点,若∠B1MN是直角,则∠C1MN等于__90°__.
[解析] 因为C1B1⊥平面ABB1A1,MN⊂平面ABB1A1,所以C1B1⊥MN.
又因为MN⊥MB1,MB1,C1B1⊂平面C1MB1,MB1∩C1B1=B1,所以MN⊥平面C1MB1,
所以MN⊥C1M,所以∠C1MN=90°.
15.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足__DM⊥PC(或BM⊥PC)__时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件即可).
[解析] 连接AC,则BD⊥AC,由PA⊥底面ABCD,可知BD⊥PA,∴BD⊥平面PAC,∴BD⊥PC.故当DM⊥PC(或BM⊥PC)时,平面MBD⊥平面PCD.
16.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为__36π__.
[解析] 如图,连接OA,OB.
由SA=AC,SB=BC,SC为球O的直径,知OA⊥SC,OB⊥SC.
由平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,OA⊥SC,知OA⊥平面SCB.
设球O的半径为r,则OA=OB=r,SC=2r,
∴三棱锥S-ABC的体积V=×(SC·OB)·OA=,
即=9,∴r=3,∴S球表=4πr2=36π.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.
(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
[解析] (1)证明:取B1D1的中点O1,连接CO1,A1O1,
由于ABCD-A1B1C1D1是四棱柱,
所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,所以A1O∥O1C,
又O1C⊂平面B1CD1,A1O⊄平面B1CD1,
所以A1O∥平面B1CD1.
(2)证明:因为AC⊥BD,E,M分别为AD和OD的中点,
所以EM⊥BD.
又A1E⊥平面ABCD,BD⊂平面ABCD,
所以A1E⊥BD,
因为B1D1∥BD,
所以EM⊥B1D1,A1E⊥B1D1.
又A1E,EM⊂平面A1EM,A1E∩EM=E,
所以B1D1⊥平面A1EM.
又B1D1⊂平面B1CD1,
所以平面A1EM⊥平面B1CD1.
18.(本小题满分12分)如图,矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D的点.
(1)证明:平面AMD⊥平面BMC;
(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.
[解析] (1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM⊂平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.
19.(本小题满分12分)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
[解析] (1)证明:因为PA⊥AB,PA⊥BC,所以PA⊥平面ABC.
又因为BD⊂平面ABC,
所以PA⊥BD.
(2)证明:因为AB=BC,D为AC的中点,所以BD⊥AC.
由(1)知,PA⊥BD,
所以BD⊥平面PAC,
所以平面BDE⊥平面PAC.
(3)解:因为PA∥平面BDE,平面PAC∩平面BDE=DE,
所以PA∥DE.
因为D为AC的中点,
所以DE=PA=1,BD=DC=.
由(1)知,PA⊥平面ABC,
所以DE⊥平面ABC,
所以三棱锥E-BCD的体积V=BD·DC·DE=.
20.(本小题满分12分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2,∠BAD=90°.
(1)求证:AD⊥BC;
(2)求异面直线BC与MD所成角的余弦值;
(3)求直线CD与平面ABD所成角的正弦值.
[解析] (1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.
(2)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.
在Rt△DAM中,AM=1,故DM==.因为AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN==.在等腰三角形DMN中,MN=1,
可得cos∠DMN==.所以,异面直线BC与MD所成角的余弦值为.
(3)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=.又因为平面ABC⊥平面ABD,而CM⊂平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.在Rt△CAD中,CD==4.
在Rt△CMD中,sin∠CDM==.所以,直线CD与平面ABD所成角的正弦值为.
21.(本小题满分12分)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.
(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
[解析] (1)解:如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.
因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.
在Rt△PDA中,由已知,得AP==,
故cos∠DAP==.
所以,异面直线AP与BC所成角的余弦值为.
(2)证明:由(1)知AD⊥PD.又因为BC∥AD,所以PD⊥BC.
又PD⊥PB,PB∩BC=B,
所以PD⊥平面PBC.
(3)解:过点D作DF∥AB,交BC于点F,连接PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,
所以PF为DF在平面PBC上的射影,
所以∠DFP为直线DF和平面PBC所成的角.
由于AD∥BC,DF∥AB,故BF=AD=1.
由已知,得CF=BC-BF=2.
又AD⊥DC,所以BC⊥DC.
在Rt△DCF中,可得DF==2,
在Rt△DPF中,可得sin∠DFP==.
所以,直线AB与平面PBC所成角的正弦值为.
22.(本小题满分12分)如图,四面体ABCD中,O,E分别为BD,BC的中点,CA=CB=CD=BD=2,AB=AD=.
(1)求证:AO⊥平面BCD;
(2)求点E到平面ACD的距离.
[解析] (1)连结OC.因为BO=DO,AB=AD,所以AO⊥BD.因为BO=DO,CB=CD,所以CO⊥BD.
在△AOC中,由已知可得AO=1,CO=.而AC=2,所以AO2+CO2=AC2,所以∠AOC=90°,即AO⊥OC.因为BD∩OC=O,所以AO⊥平面BCD.
(2)设点E到平面ACD的距离为h.因为VE-ACD=VA-CDE,所以h·S△ACD=·AO·S△CDE.
在△ACD中,CA=CD=2,AD=,所以S△ACD=××=.
而AO=1,S△CDE=××22=,所以h===.
所以点E到平面ACD的距离为.
人教版新课标A第二章 基本初等函数(Ⅰ)综合与测试当堂检测题: 这是一份人教版新课标A第二章 基本初等函数(Ⅰ)综合与测试当堂检测题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中第二章 平面向量综合与测试同步测试题: 这是一份高中第二章 平面向量综合与测试同步测试题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
人教A版高中数学必修2-本册综合学业质量标准检测: 这是一份数学必修2本册综合测试题,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。














