2021年福建省漳州市七年级上学期数学期中试卷附答案

这是一份2021年福建省漳州市七年级上学期数学期中试卷附答案，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

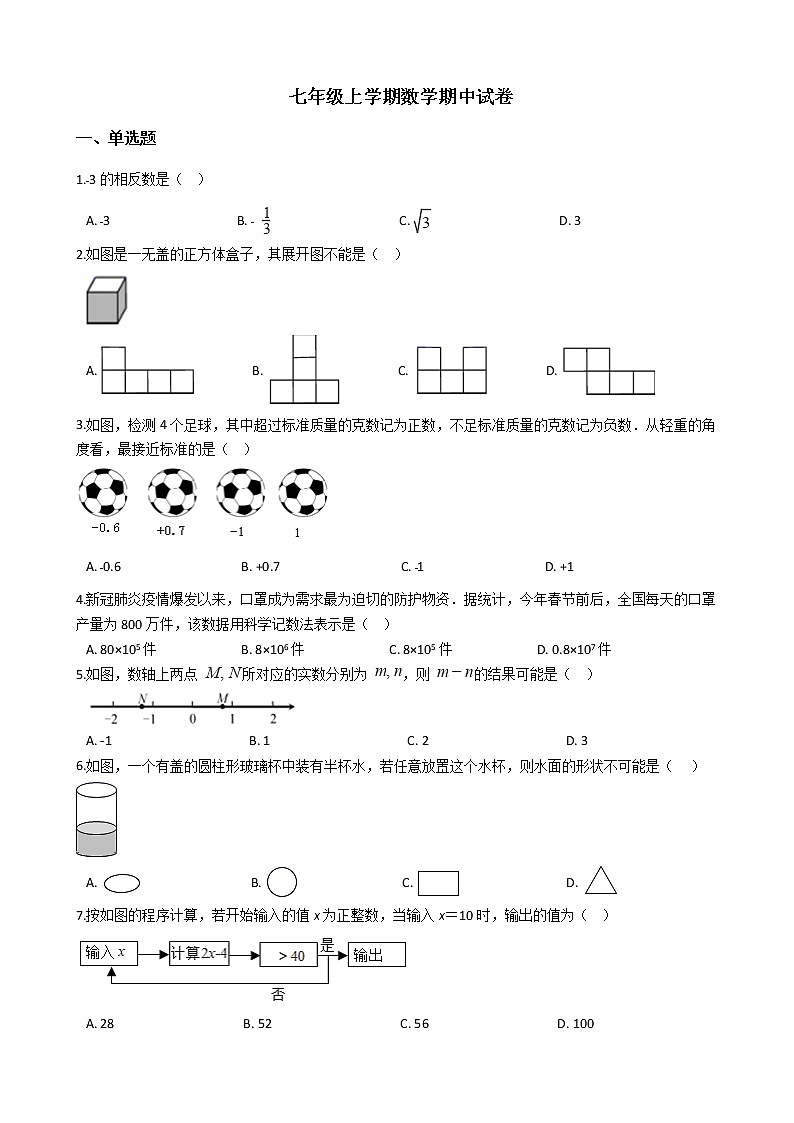
1.﹣3的相反数是（ ）
A. ﹣3 B. ﹣ C. D. 3
2.如图是一无盖的正方体盒子，其展开图不能是（ ）
A. B. C. D.
3.如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数．从轻重的角度看，最接近标准的是（ ）
A. ﹣0.6 B. +0.7 C. ﹣1 D. +1
4.新冠肺炎疫情爆发以来，口罩成为需求最为迫切的防护物资．据统计，今年春节前后，全国每天的口罩产量为800万件，该数据用科学记数法表示是（ ）
A. 80×105件 B. 8×106件 C. 8×105件 D. 0.8×107件
5.如图，数轴上两点 所对应的实数分别为 ，则 的结果可能是（ ）
A. -1 B. 1 C. 2 D. 3
6.如图，一个有盖的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是（ ）
A. B. C. D.
7.按如图的程序计算，若开始输入的值x为正整数，当输入x＝10时，输出的值为（ ）
A. 28 B. 52 C. 56 D. 100
8.若|m|＝3，n2＝25，且m﹣n＞0，则m+n的值为（ ）
A. ±8 B. ±2 C. 2或8 D. ﹣2或﹣8
9.有一个正方体的六个面上分别标有数字1、2、3、4、5、6，从三个不同的角度观察这个正方体所得到的结果如图所示，如果标有数字6的面所对面上的数字记为a，2的面所对面上数字记为b，那么a+b的值为（ ）
A. 6 B. 7 C. 8 D. 9
10.一根 长的绳子，第一次剪去绳子的 ，第二次剪去剩下绳子的 ，如此剪下去，第100次剪完后剩下绳子的长度是（ ）
A. B. C. D.
二、填空题
11.某日中午，气温由早晨的零下2℃上升了10℃，傍晚又下降了3℃，这天傍晚气温是________．
12.现定义一种新运算“*”，规定a*b＝a2﹣b ， 如3*1＝32﹣1，则（﹣2）*（﹣3）等于________．
13.如下图，用含a、b的代数式表示图中阴影部分的面积________．
14.数轴上，到2的距离等于4个单位长度的点所表示的数是________.
a ， b在数轴上的对应点如图所示，则下面式子中正确的是________．
①a＜0＜b；②|a|＜|b|；③ab＞0；④b﹣a＞b+a ．
16.如图，将直径为1个单位长度的圆沿着数轴向右滚动一周，圆上一点由表示﹣2的点A到达点A'，则点A'对应的数是________．
三、解答题
17.计算：
（1）12﹣（﹣7）+（﹣6）﹣13；
（2）；
（3）﹣10﹣|﹣8|÷（﹣2）×（﹣ ）；
（4）．
18.作图题：（作图请用直尺，否则不得分）如图是由一些大小相同的小正方体组合成的简单几何体，请你在给定的方格纸内分别画出从左面和从上面看到的平面图形
19.将下列各数在数轴上表示出来，并用“＜”连接：
﹣22 ， ﹣（﹣1），0，2.5，﹣|﹣2|．
20.如图，这是某个几何体从三个不同方向所看到的图形.
（1）说出这个立体图形的名称；
（2）根据图中的有关数据，求这个几何体的侧面积.
21.新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控工作．某药店出售口罩和消毒液，N95口罩每盒定价300元，75%酒精消毒液每瓶定20元，药店开展优惠活动，向客户提供两种优惠方案：
①买一盒口罩送一瓶消毒液；
②口罩和消毒液都按定价的95%付款．
某客户购买口罩10盒，酒精消毒液x瓶（x＞10）．
（1）客户分别按方案①、方案②购买，各需付款多少元？（用含x的代数式表示）；
（2）若x＝30时，通过计算说明此时按哪种方案购买更优惠？
22.我县出租车的计价标准为：行驶路程不超过3千米收费7元，超过3千米的部分按每千米2元收费．
（1）若某人乘坐了x（x＞3）千米，则他应支付车费________元（用含有x的代数式表示）；
（2）一出租车公司坐落于东西向的大道边，驾驶员王师傅从公司出发，在此大道上连续接送了4批客人，行驶记录如下：（规定向东为正，向西为负，单位：千米）．
送完第4批客人后，王师傅在公司的________边（填“东”或“西”），距离公司________千米的位置；
（3）①若王师傅的车平均每千米耗油0.1升，则送完第4批客人后，王师傅用了多少升油？
②在整个过程中，王师傅共收到车费多少元？
23.综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为acm的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒），请你动手操作验证并完成任务．（纸板厚度及接缝处忽略不计）
动手操作一：
根据图1方式制作一个无盖的长方体盒子．方法：先在纸板四角剪去四个同样大小边长为bcm的小正方形，再沿虚线折合起来．
问题解决：
（1）该长方体纸盒的底面边长为________cm；（请你用含a ， b的代数式表示）
（2）若a＝24cm ， b＝6cm ， 则长方体纸盒的底面积为多少cm2；
（3）该长方体纸盒的体积为多少cm3？（请你用含a ， b的代数式表示）
A表示数a ， 点B表示数b ， 点C表示数c；a是最大的负整数，a、b、c满足|a+b|+（c﹣5）2＝0．
（1）填空：a＝________，b＝________，c＝________；
（2）P为数轴上一动点，其对应的数是x ， 当P在线段AC上，且PA+PB+PC＝7时，求x的值．
（3）若点P ， Q分别从A ， C同时出发，匀速相向运动，点P的速度为3个单位/秒，点Q的速度为1个单位/秒．当点P运动到C后迅速以原速返回A；点Q运动至B点后停止运动，同时P点也停止运动．求在此运动过程中P ， Q的相遇点在数轴上对应的数．
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解：-3的相反数是3
故答案为：D．
【分析】利用相反数的定义得出即可．
2.【答案】 C
【解析】【解答】解：由四棱柱四个侧面和底面的特征可知，A、B、D可以拼成无盖的正方体，而C拼成的是上下都无底，且有一面重合的立体图形.
故一个无盖的正方体盒子的平面展开不可以是选项中的C.
故答案选：C

【分析】根据正方体表面展开图的特征：一线不过四，田凹应弃之即可求解。
3.【答案】 A
【解析】【解答】解：∵|﹣0.6|＝0.6，|+0.7|＝0.7，|﹣1|＝1，|+1|＝1，
而0.6最小，
∴﹣0.6最接近标准，
故答案为：A ．

【分析】算出每个数据的绝对值，再比较大小，取最小即可。
4.【答案】 B
【解析】【解答】解：800万＝8000000＝8×106 ．
故答案为：B ．

【分析】利用科学记数法的定义及书写要求求解即可。
5.【答案】 C
【解析】【解答】解：根据数轴可得 ＜ ＜1， ＜ ＜ ，则1＜ ＜3
故答案为：C
【分析】根据数轴确定m和n的范围，再根据有理数的加减法即可做出选择．
6.【答案】 D
【解析】【解答】解：将这杯水斜着放可得到A选项的形状，
将水杯倒着放可得到B选项的形状，
将水杯正着放可得到C选项的形状，
不能得到三角形的形状，
故答案为：D．
【分析】根据圆柱体的截面图形可得．
7.【答案】 B
【解析】【解答】解：依据题中的计算程序，当x＝10时，2×10﹣4＝16，
由于16＜40，需再次输入，
∴当x＝16时，2×16﹣4＝28，
由于28＜40，仍需再次输入，
∴当x＝28时，2×28﹣4＝52，
由于52＞40，可以输出．
故答案为：B ．

【分析】将x的值代入流程图计算即可。
8.【答案】 D
【解析】【解答】解：由题意得：m＝±3，n＝±5，
由m﹣n＞0，得到m＞n ，
∴m＝3，n＝﹣5或m＝﹣3，n＝﹣5，
则m+n＝﹣2或﹣8．
故答案为：D ．

【分析】根据绝对值的性质及平方根求出m、n的值，再代入计算即可。
9.【答案】 B
【解析】【解答】解：从图可以看出1和6、4、3、2都相邻，所以1的对面只能是5，
4和1、6、5、3相邻，那么4的对面是2，即2的对面是4，
由以上两项可知6和3相对，即6的对面是3，
所以a+b=3+4=7.
故答案为：B.

【分析】 由图一和图二可看出1的相对面是5，再由图二和图三可看出3的相对面是6，从而2的相对面是4，得出a=3，b=4，即可求出 a+b的值 ．
10.【答案】 C
【解析】【解答】∵第一次剪去绳子的 ，还剩 原长
第二次剪去剩下绳子的 ，还剩 上次剩下的长度
因此每次减绳子后的长度都是上次剩下长度的
根据乘方的定义，我们得出第n次剪去绳子的 ，还剩
第100次剪去绳子的 ，还剩
故答案为：C．
【分析】根据题意得每次减绳子后的长度都是上次剩下长度的 ，根据乘方的定义我们可以得出关于x的关系式，代入 求解即可．
二、填空题
11.【答案】 5℃
【解析】【解答】∵某日中午，气温由早晨的零下2℃上升了10℃，
∴中午的温度是：﹣2+10＝8（℃），
∵傍晚又下降了3℃，
∴这天傍晚气温是：8﹣3＝5（℃）．
故答案为：5℃．

【分析】直接根据题干，列出算式，利用有理数的加减计算即可。
12.【答案】 7
【解析】【解答】解：∵a*b＝a2﹣b ，
∴（﹣2）*（﹣3）
＝（﹣2）2﹣（﹣3）
＝4+3
＝7，
故答案为：7．

【分析】根据题干中给出的计算方法代入计算即可。
13.【答案】
【解析】【解答】阴影部分面积＝ab− ＝ ．
故答案为： ．

【分析】用长方形的面积减去半圆的面积即可。
14.【答案】 6或﹣2
【解析】【解答】解：当所求点在表示2的点的左边时，此时所求的数为：2－4=－2；
当所求点在表示2的点的右边时，此时所求的数为：2+4=6；
故答案为：6或﹣2.
【分析】分当所求的点在表示2的点的左边或右边时两种情况，分别列出算式求出即可.
15.【答案】 ①④
【解析】【解答】由数轴可知：a＜0＜b ， 且|a|＞|b|，故①符合题意；②不符合题意；
∴ab＜0，故③不符合题意；
b﹣a＞0，b+a＜0，
∴b﹣a＞b+a ， 故④符合题意．
故答案为①④．

【分析】先利用数轴判断出a、b的正负及大小，再逐项判断即可。
16.【答案】 π﹣2
【解析】【解答】由题意可得：滚动的距离即为圆的周长

∵A所表示的数为﹣2，
所表示的数为π﹣2
故答案是：π﹣2

【分析】利用圆周长的计算公式求出点A走的路程，再加上-2即是点A'表示的数。
三、解答题
17.【答案】 （1）解：12﹣（﹣7）+（﹣6）﹣13
＝12+7+（﹣6）+（﹣13）
＝（12+7）+[（﹣6）+（﹣13）]
＝19+（﹣19）
＝0；
（2）解：
＝36×（﹣ ）+36× +36×（﹣ ）
＝（﹣8）+27+（﹣15）
＝4；
（3）解：﹣10﹣|﹣8|÷（﹣2）×（﹣ ）
＝﹣10﹣8×（﹣ ）×（﹣ ）
＝﹣10﹣2
＝﹣12；
（4）解：
＝﹣1×（3﹣4）+3×（﹣ ）
＝﹣1×（﹣1）+（﹣4）
＝1+（﹣4）
＝﹣3．
【解析】【分析】（1）利用有理数的交换律及结合律求解即可；（2）利用有理数乘法的运算律求解即可；（3）先计算乘除，最糊计算减法即可；（4）先计算乘方，再算括号及乘除，最后算加减即可。
18.【答案】 解：如图所示：
【解析】【分析】根据三视图的定义作图即可。
19.【答案】 解：﹣22 ， ＝﹣4，﹣（﹣1）＝1，﹣|﹣2|＝﹣2，在数轴上表示如图所示：
用“＜”连接为：﹣22＜﹣|﹣2|＜0＜﹣（﹣1）＜2.5．
【解析】【分析】先化简，再将数据在数轴上表示出来，最后利用数轴上右边的数大于左边的数求解即可。
20.【答案】 （1）解：根据三视图可得：这个立体图形是三棱柱；
（2）解：表面积为： .
【解析】【分析】(1)根据三视图可直接得出这个立体图形是三棱柱；(2)根据直三棱柱的表面积公式进行计算即可．
21.【答案】 （1）解：方案①需付费为：300×10+（x﹣10）×20＝20x+2800（元）；
方案②需付费为：（300×10+20x）×0.95＝19x+2850（元）；
（2）解：当x＝30元时，
方案①需付款为：20x+2800＝20×30+2800＝3400（元），
方案②需付款为：19x+2850＝19×30+2850＝3420（元），
∵3400＜3420，
∴选择方案①购买较为合算．
【解析】【分析】（1）根据题干中的方案的计算方法列出表达式即可；（2）激昂x=30分别代入（1）中的两个代数式，再比较大小即可。
22.【答案】 （1）（2x+1）
（2）西；6
（3）①（|+2.1|+|﹣6|+|+2.9|+|﹣5|）×0.1
＝1.6（升）．
答：送完第4批客人后，王师傅用了1.6升油；
②在整个过程中，王师傅共收到车费：7+[7+（6﹣3）×2]+7+[7+（5﹣3）×2]＝38（元）．
故王师傅共收到车费38元．
【解析】【解答】解：（1）由题意可得，
他应支付车费：7+（x﹣3）×2＝（2x+1）元．
故答案为：（2x+1）；解：（2）（+2.1）+（﹣6）+（+2.9）+（﹣5）＝﹣6，
即送完第4批客人后，王师傅在公司的西边，距离公司6千米．
故答案为：西，6；

【分析】（1）根据题意，可以用含x的表达式表示出某人应支付的车费；（2）将表格中的数据相加，根据结果的正负判断即可；（3）①将表格中的数据的绝对值相加，再乘以0.1即可；②根据表格中的数据，判断每一批的车费，再相加即可。
23.【答案】 （1）（a﹣2b）
（2）解：将a＝24，b＝6代入得，（a﹣2b）2＝（24﹣2×6）2＝144（cm2）
答：长方体纸盒的底面积为144cm2；
动手操作二：
根据图2方式制作一个有盖的长方体纸盒．
方法：先在纸板四角剪去两个同样大小边长为bcm的小正方形和两个同样大小的小长方形，再沿虚线折合起来．
拓展延伸：
（3）解：裁剪后折叠成长方体的长为：（a﹣2b）cm，宽为 cm，高为bcm，
所以，折叠后长方体的体积为（a﹣2b）× ×b，即， b（a﹣2b）2 ，
答：长方体的体积为 b（a﹣2b）2 ．
【解析】【解答】解：（1）根据折叠可知，底面是边长为（a﹣2b）的正方形，
故答案为：（a﹣2b）；

【分析】（1）根据折叠的性质即可求解；（2）将a、b的值代入底面积的代数式求解即可；（3）根据图2的裁剪，折叠后，表示出长、宽、高，即可求出长方体的体积。
24.【答案】 （1）﹣1；1；5
（2）解：∵PA+PB+PC＝7，
∴|x+1|+|x﹣1|+|x﹣5|＝7，
①当点P在线段AB上，即当﹣1≤x＜1时，
x+1+1﹣x+5﹣x＝7，
解得：x＝0；
②当点P在线段BC上，即当1≤x≤5时，
x+1+x﹣1+5﹣x＝7，
解得：x＝2．
综上所述，x的值是0或2．
（3）解：设运动时间为t，
①当P、Q第一次相遇时，有：
3t+t＝5﹣（﹣1），
解得：t＝1.5，
此时，相遇点在数轴上对应的数为5﹣1.5＝3.5；
②当P到达C点返回追上Q时，有：3t﹣t＝5﹣（﹣1）
解得：t＝3，
此时，相遇点在数轴上对应的数为5﹣3＝2．
∴在此运动过程中P，Q的相遇点在数轴上对应的数是3.5或2．
【解析】【解答】解：（1）∵a是最大的负整数，
∴a＝﹣1；
∵|a+b|+（c﹣5）2＝0，
|a+b|≥0，（c﹣5）2≥0，
∴a+b＝0，c﹣5＝0，
∴b＝﹣a＝﹣（﹣1）＝1，c＝5．
故答案为：﹣1，1，5；

【分析】（1）根据a是最大的负整数，非负数之和为0的性质求出a、b、c的值；（2）根据PA+PB+PC＝7，结合数轴上色两点所表示的距离的公式，分类去掉绝对值，并分别解出x的值范围即可；（3）设运动时间为t，分两种情况分别得出关于t的方程并求解即可。第1批
第2批
第3批
第4批
﹣6
﹣5