

专题04 不等式 题型归纳讲义-2022届高三数学一轮复习(解析版)学案
展开这是一份专题04 不等式 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共15页。学案主要包含了均值不等式的常见变形等内容,欢迎下载使用。
专题四 《不等式》讲义
知识梳理.不等式
1.不等式的性质
(1)对称性:a>b⇔b
(3)可加性:a>b⇔a+cb+c;a>b,c>d⇒a+c>b+d;
(4)可乘性:①a>b,c>0⇒ac>bc; ②a>b>0,c>d>0⇒ac>bd;
(5)可乘方性:a>b>0⇒anbn(n∈N,n≥1);
(6)可开方性:a>b>0⇒(n∈N,n≥2).
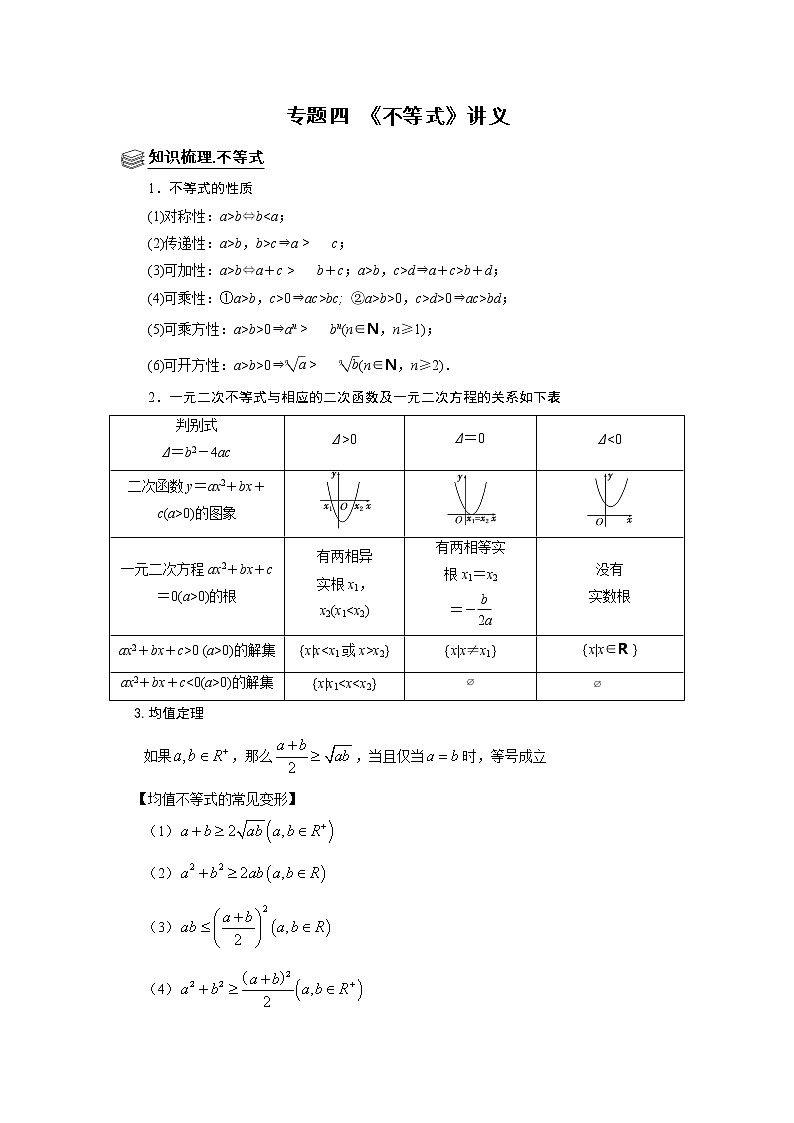
2.一元二次不等式与相应的二次函数及一元二次方程的关系如下表
判别式
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c(a>0)的图象
一元二次方程ax2+bx+c=0(a>0)的根
有两相异
实根x1,
x2(x1
根x1=x2
=-
没有
实数根
ax2+bx+c>0 (a>0)的解集
{x|x
{x|x≠x1}
{x|x∈R }
ax2+bx+c<0(a>0)的解集
{x|x1
3.均值定理
如果,那么,当且仅当时,等号成立
【均值不等式的常见变形】
(1)
(2)
(3)
(4)
题型一. 不等式的性质
1.下列命题中,正确的是( )
A.若ac<bc,则a<b B.若a>b,c>d,则ac>bd
C.若a>b>0,则a2>b2 D.若a<b,c<d,则a﹣c<b﹣d
【解答】解:对于A,由ac<bc,c>0时,a<b;c<0时,a>b,所以A错误;
对于B,当a>b>0,c>d>0时,有ac>bd,所以B错误;
对于C,当a>b>0时,有a2>b2,所以C正确;
对于D,由a<b,c<d,得出﹣d<﹣c,所以a﹣d<b﹣c,D错误.
故选:C.
2.设a,b∈R,则“a<b”是“(a﹣b)a2<0”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【解答】解:若a=0,b=1,满足a<b,但(a﹣b)a2<0不成立,
若“(a﹣b)a2<0,则a<b且a≠0,则a<b成立,
故“a<b”是“(a﹣b)a2<0”的必要不充分条件,
故选:B.
3.若1a<1b<0,有下面四个不等式:①|a|>|b|;②a<b;③a+b<ab,④a3>b3,不正确的不等式的个数是( )
A.0 B.1 C.2 D.3
【解答】解:由1a<1b<0,可得 0>a>b,∴|a|<|b|,故①②不成立;
∴a+b<0<ab,a3>b3都成立,故③④一定正确,
故选:C.
4.7+3与6+10的大小关系是( )
A.7+3<6+10 B.7+3>6+10 C.7+3=6+10 D.不确定
【解答】解:(7+3)2=16+67=16+252,(6+10)2=16+260=16+240,
∴(7+3)2>(6+10)2,
∴7+3>6+10.
故选:B.
5.已知a>b>1,0<c<1,下列不等式成立的是( )
A.ca>cb B.ac<bc
C.logca>logbc D.bac<abc
【解答】解:对于A,因为0<c<1,所以指数函数f(x)=cx是减函数,
又a>b,所以f(a)<f(b),即ca<cb,故A错误;
对于B,因为a>b,c>0,所以ac>bc,故B错误;
对于C,取a=4,b=2,c=12,
则logca=log124=-2,logbc=log212=-1,logca<logbc,故C错误;
对于D,由a>b>1,可得0<ba<1,
又0<c<1,所以(ba)1<(ba)c,即bac<abc,故D正确.
故选:D.
6.若实数x,y满足x>y>0,则( )
A.1y>1x B.ln(x﹣y)>lny
C.x+y<2(x2+y2) D.x﹣y<ex﹣ey
【解答】解:因为x>y>0,所以1y>1x,A正确;
由于x﹣y与y的大小不确定,B不正确;
因为2(x2+y2)﹣(x+y)2=x2+y2﹣2xy=(x﹣y)2>0,
所以2(x2+y2)>(x+y)2,C正确;
令f(x)=ex﹣x,则f′(x)=ex﹣1>0,
故f(x)在(0,+∞)上单调递增,
由x>y>0,得f(x)>f(y),
所以ex﹣x>ey﹣y,
所以x﹣y<ex﹣ey,D正确.
故选:ACD.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/6/9 17:30:47;用户:15942715433;邮箱:15942715433;学号:32355067
题型二. 一元二次不等式
1.集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<32},则A∩B为( )
A.{x|12<x≤32} B.{x|1<x≤32} C.{x|12≤x≤32} D.{x|12≤x<32}
【解答】解:由A中的不等式变形得:2x2﹣5x+2≤0,即(2x﹣1)(x﹣2)≤0,
解得:12≤x≤2,即A={12≤x≤2};
∵B={x|﹣1<x<32},
∴A∩B={x|12≤x<32}.
故选:D.
2.关于x的不等式x2﹣(a+1)x+a<0的解集中恰有一个整数.则实数a的取值范围是( )
A.{a|﹣1<a≤0或2≤a<3} B.{a|﹣2<a≤﹣1或3<a≤4}
C.{a|﹣1≤a<0或2<a≤3} D.{a|﹣2<a<﹣1或3<a<4}
【解答】解:不等式x2﹣(a+1)x+a<0可化为(x﹣1)(x﹣a)<0;
当a=1时,不等式的解集为空集,不符合题意;
当a>1时,不等式的解集为{x|1<x<a},由解集中恰有一个整数,则实数a满足2<a≤3;
当a<1时,不等式的解集为{x|a<x<1},由解集中恰有一个整数,则实数a满足﹣1≤a<0;
综上知,实数a的取值范围是{a|﹣1≤a<0或2<a≤3}.
故选:C.
3.如果不等式ax2+bx+c>0的解集为{x|﹣2<x<4},那么对于函数f(x)=ax2+bx+c应有( )
A.f(5)<f(2)<f(﹣1) B.f(﹣1)<f(5)<f(2)
C.f(2)<f(﹣1)<f(5) D.f(5)<f(﹣1)<f(2)
【解答】解:∵不等式ax2+bx+c>0的解集为{x|﹣2<x<4},
∴a<0,﹣2,4是ax2+bx+c=0的两个实数根,
∴﹣2+4=-ba,﹣2×4=ca.
那么对于函数f(x)=ax2+bx+c=a(x2﹣2x﹣8)=a(x﹣1)2﹣9a,(a<0).
此抛物线开口向下,其图象关系直线x=1对称,
∴f(﹣1)=f(3),f(2)>f(3)>f(5),
∴f(2)>f(﹣1)>f(5),
故选:D.
4.关于x的不等式x2+ax﹣2<0在区间[1,4]上有解,则实数a的取值范围为( )
A.(﹣∞,1) B.(﹣∞,1] C.(1,+∞) D.[1,+∞)
【解答】解:关于x的不等式x2+ax﹣2<0在区间[1,4]上有解,
等价于a<(2x-x)max,x∈[1,4];
设f(x)=2x-x,x∈[1,4],
则函数f(x)在x∈[1,4]单调递减,
且当x=1时,函数f(x)取得最大值f(1)=1;
所以实数a的取值范围是(﹣∞,1).
故选:A.
5.如果关于x的不等式(a﹣2)x2+2(a﹣2)x﹣4<0对一切实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,2] B.(﹣∞,﹣2) C.(﹣2,2] D.(﹣2,2)
【解答】解:关于x的不等式(a﹣2)x2+2(a﹣2)x﹣4<0对一切实数x恒成立,
当a=2时,对于一切实数x,不等式(a﹣2)x2+2(a﹣2)x﹣4<0恒成立;
当a≠2时,要使对于一切实数x,不等式(a﹣2)x2+2(a﹣2)x﹣4<0恒成立,
则a-2<0[2(a-2)]2-4(a-2)(-4)<0,解得:﹣2<a<2.
综上,实数a的取值范围是(﹣2,2].
故选:C.
6.已知不等式(x2﹣ax+1)(lnx﹣a)≤0在x∈[1,2]上恒成立,则实数a的取值范围为 [ln2,2] .
【解答】解:若(x2﹣ax+1)(lnx﹣a)≤0,
则①x2﹣ax+1≥0且lnx﹣a≤0,
由x2﹣ax+1≥0,得:a≤x+1x,
由y=x+1x在[1,2]递增,得:a≤2,
由a≥lnx得:a≥ln2,
故ln2≤a≤2;
②x2﹣ax+1≤0且lnx﹣a≥0,
由x2﹣ax+1≤0,得:a≥x+1x,
由y=x+1x在[1,2]递增,得:a≥52,
由a≤lnx得:a≤ln1=0,无解
故a的取值范围是[ln2,2],
故答案为:[ln2,2].
题型三. 基本不等式
考点1.和定积最大、积定和最小
1.已知a>0,b>0,且满足a3+b4=1,则ab的最大值是( )
A.2 B.3 C.4 D.6
【解答】解:∵a>0,b>0,且满足a3+b4=1,
∴1≥2a3⋅b4,化为:ab≤3,当且仅当a=32,b=2时取等号.
则ab的最大值是3.
故选:B.
2.已知x>0,则y=x+1x+1的最小值是( )
A.2 B.3 C.4 D.6
【解答】解:∵x>0,
∴y=x+1x+1≥2x⋅1x+1=3,当且仅当x=1时取等号.
∴y=x+1x+1的最小值是3.
故选:B.
3.已知0<x<2,则y=x4-x2的最大值为( )
A.2 B.4 C.5 D.6
【解答】解:0<x<2,可得4﹣x2>0,
则y=x4-x2≤x2+4-x22=2,
当且仅当x2=4﹣x2,即x=2时,上式取得等号,
即有函数y的最大值为2.
故选:A.
考点2.凑定值
1.已知0<x<12,则函数y=x(1﹣2x)的最大值是( )
A.12 B.14 C.18 D.19
【解答】解:∵0<x<12,
∴x(1﹣2x)=12•2x(1﹣2x)≤12•[2x+(1-2x)2]2=18,
当且仅当2x=1﹣2x时,即x=14时等号成立,
因此,函数y=x(1﹣2x)的最大值为f(14)=18,
故选:C.
2.已知x<54,求函数y=4x﹣1+14x-5的最大值.
【解答】解:根据题意,函数y=4x﹣5+14x-5+4=﹣[(5﹣4x)+15-4x]+4,
又由x<54,则5﹣4x>0,
则(5﹣4x)+15-4x≥2(5-4x)×15-4x=2,
则y=﹣[(5﹣4x)+15-4x]+4≤﹣2+4=2,
故函数y=4x﹣1+14x-5的最大值为2.
考点3. 1的代换
1.已知a>0,b>0,且a+2b=ab,则ab的最小值是( )
A.4 B.8 C.16 D.32
【解答】解:∵已知a>0,b>0,且a+2b=ab,∴ab≥2a⋅2b.
化简可得ab≥22,
∴ab≥8,当且仅当a=2b时等号成立,
故ab的最小值是8,
故选:B.
2.若正数a,b满足2a+b=1,则a2-2a+b2-b的最小值是 223-12 .
【解答】解:设u=2﹣2a,v=2﹣b,则a=2-u2,b=2﹣v,
u+v=3,(u,v>0),
即有a2-2a+b2-b=1-12uu+2-vv
=1u+2v-32=13(u+v)(1u+2v)-32
=13(3+vu+2uv)-32≥13(3+2vu⋅2uv)-32
=1+223-32=223-12.
当且仅当v=2u=6﹣32时,取得最小值.
故答案为:223-12.
3.已知实数x>0,y>0,且满足x+y=1,则2x+xy的最小值为 2+22 .
【解答】解:∵实数x>0,y>0,且满足x+y=1,
则2x+xy=2(x+y)y+xy=2+2yx+xy≥2+22yx⋅xy=2+22,当且仅当x=2y=2-2时取等号.
故答案为:2+22.
日期:2021/6/15 22:31:08;用户:15942715433;邮箱:15942715433;学号:32355067
考点4. x、y、xy型
1.如果x>0,y>0,x+y+xy=2,则x+y的最小值为 23-2 .
【解答】解:已知x>0,y>0,且x+y+xy=2
即:xy=2﹣(x+y),
利用基本不等式:xy≤(x+y2)2.
∴2﹣(x+y)≤(x+y2)2.
解之得:x+y≥23-2
则x+y的最小值为23-2.
故答案为23-2.
2.已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为 4 .
【解答】解:考察基本不等式x+2y=8﹣x•(2y)≥8﹣(x+2y2)2(当且仅当x=2y时取等号)
整理得(x+2y)2+4(x+2y)﹣32≥0
即(x+2y﹣4)(x+2y+8)≥0,又x+2y>0,
所以x+2y≥4(当且仅当x=2y时即x=2,y=1时取等号)
则x+2y的最小值是4.
故答案为:4.
3.设x,y∈R,若4x2+y2+xy=1,则2x+y的最大值是 2105 .
【解答】解:∵4x2+y2+xy=1,∴4x2+y2+4xy=1+3xy,
∴(2x+y)2=1+3xy=1+32•2x•y≤1+32•(2x+y2)2,
整理可得58(2x+y)2≤1,
解关于2x+y的一元二次不等式可得-2105≤2x+y≤2105
∴2x+y的最大值为:2105
4.若a,b,c>0且a2+2ab+2ac+4bc=12,则a+b+c的最小值是 23 .
【解答】解:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=12+(b﹣c)2≥12,
当且仅当b=c时取等号,
∴a+b+c≥23
故答案为:23
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/6/15 22:36:45;用户:15942715433;邮箱:15942715433;学号:32355067
考点5. y=1a+ab型函数的最值
1.设a+b=2,b>0,则当a= ﹣2 时,12|a|+|a|b取得最小值.
【解答】解:法一:
∵a+b=2,b>0,
∴12|a|+|a|b=12|a|+|a|2-a,(a<2)
设f(a)=12|a|+|a|2-a,(a<2),画出此函数的图象,如图所示.
利用导数研究其单调性得,
当a<0时,f(a)=-12a+aa-2,
f′(a)=12a2-2(a-2)2=-(3a-2)(a+2)2a2(a-2)2,当a<﹣2时,f′(a)<0,当﹣2<a<0时,f′(a)>0,
故函数在(﹣∞,﹣2)上是减函数,在(﹣2,0)上是增函数,
∴当a=﹣2时,12|a|+|a|b取得最小值34.
同样地,当0<a<2时,得到当a=23时,12|a|+|a|b取得最小值54.
综合,则当a=﹣2时,12|a|+|a|b取得最小值.
法二:
因为a+b=2,b>0,
要取得最小值,则a<0,
则12|a|+|a|b=a+b4|a|+|a|b=a4|a|+b4|a|+|a|b,
≥a4|a|+2b4|a|⋅|a|b=a4|a|+1=-14+1=34,
当且仅当b4|a|=|a|b,a<0时取等号,此时b=﹣2a,
因为a+b=2,
所以a=﹣2,b=4,
故答案为:﹣2.
2.若正数a,b满足1a+1b=1,则4a-1+16b-1的最小值为 16 .
【解答】解:正数a,b满足1a+1b=1,
则有1a=1-1b=b-1b,
则有1b-1=ab,
1b=1-1a=a-1a,即有1a-1=ba,
则有4a-1+16b-1=4ba+16ab≥24ba⋅16abb=16,
当且仅当4ba=16ab即有b=2a,又1a+1b=1,
即有a=32,b=3,取得最小值,且为16.
故答案为:16.
3.设x>0,y>0,x+y﹣x2y2=4,则1x+1y的最小值为 4 .
【解答】解:∵x+y﹣x2y2=4
∴x+y=x2y2+4则1x+1y=x+yxy=x2y2+4xy=xy+4xy≥2xy×4xy=4
当且仅当xy=2时取等号
故1x+1y的最小值为4
故答案为:4
4.对于c>0,当非零实数a,b满足4a2﹣2ab+b2﹣c=0且使|2a+b|最大时,1a+2b+4c的最小值为 ﹣1 .
【解答】解:∵4a2﹣2ab+b2﹣c=0,
∴c4=(a-b4)2+316b2
由柯西不等式得,[(a-b4)2+(3b4)2][22+(23)2]≥[2(a-b4)+3b4×23]2=|2a+b|2
故当|2a+b|最大时,有a-b42=3b423
∴a=12b,c=b2
∴1a+2b+4c=2b+2b+4b2=4(1b+12)2-1
当b=﹣2时,取得最小值为﹣1.
故答案为:﹣1
题型四.不等式恒成立问题
1.若关于x的不等式ax2﹣2ax+1<0的解集为∅,则实数a的取值范围是( )
A.a>1 B.a≥1 C.0<a≤1 D.0≤a≤1
【解答】解:当a=0时,不等式化为1<0,满足解集为∅;
当a≠0时,应满足a>0△=4a2-4a≤0,
解得a>00≤a≤1,
即0<a≤1;
综上知,实数a的取值范围是0≤a≤1.
故选:D.
2.已知关于x的不等式ax2﹣2x+4a<0在(0,2]上有解,则实数a的取值范围是( )
A.(-∞,12) B.(12,+∞) C.(﹣∞,2) D.(2,+∞)
【解答】解:x∈(0,2]时,不等式可化为a<2xx2+4=2x+4x,
则f(x)=2x+4x在(0,2]上单调递增,当x=2时,f(x)取得最大值f(2)=12,
则a<f(x)max=224=12,
综上所述,实数a的取值范围是(-∞,12).
故选:A.
3.设a∈R,若x>0时均有(x2+ax﹣5)(ax﹣1)≥0成立,则a= 12 .
【解答】解:若a≤0,则当x>0时,ax﹣1<0,
由二次函数的性质可知,
不等式x2+ax﹣5≤0不可能在x>0时恒成立,
故当x>0时不可能都有(x2+ax﹣5)(ax﹣1)≥0成立,
故a>0,
故当0<x<1a时,ax﹣1<0,
当x>1a时,ax﹣1>0,
∵当x>0时均有(x2+ax﹣5)(ax﹣1)≥0成立,
故当0<x<1a时,x2+ax﹣5≤0,
当x>1a时,x2+ax﹣5≥0,
故x=1a是方程x2+ax﹣5=0的实数根,
故1a2+1﹣5=0,解得:a=-12(舍)或a=12,
综上:a=12,
故答案为:12.
4.若a,b∈R,且a>0,b>0,则下列不等式中恒成立的是( )
A.a2+b2>2ab B.a+b≥2ab C.1a+1b≥2ab D.2ba+a8b≥2
【解答】解:对于A,根据重要不等式a2+b2≥2ab,当且仅当a=b时,等号成立;故A不恒成立;
对于B,利用基本不等式,当a>0,b>0时,a+b≥2ab成立,故B正确;
对于C,利用基本不等式,当a>0,b>0时,1a+1b≥21ab=2ab成立,故C正确;
对于D,利用基本不等式,当a>0,b>0时,2ba+a8b≥22ba×a8b=1成立,故D不恒成立.
故选:BC.
5.设正实数x,y满足x>12,y>1,不等式4x2y-1+y22x-1≥m恒成立,则m的最大值为 8 .
【解答】解:设y﹣1=b,得y=b+1,
令2x﹣1=a,得x=12(a+1),则a>0,b>0;
那么:4x2y-1+y22x-1=(a+1)2b+(b+1)2a≥2•(a+1)(b+1)ab
=2•ab+(a+b)+1ab
=2•(ab+1ab+a+bab)≥2•(2ab⋅1ab+2abab)
=2•(2+2)=8;
当且仅当a=b=1,即x=2,y=1时取等号;
∴4x2y-1+y22x-1的最小值为8,
即m的最大值为8.
故答案为:8.
6.设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a,若∃x0∈R,使得f(x0)<0和g(x0)<0同时成立,则a的取值范围为( )
A.(7,+∞) B.(6,+∞)∪(﹣∞,﹣2)
C.(﹣∞,﹣2) D.(7,+∞)∪(﹣∞,﹣2)
【解答】解:由f(x)=x2﹣ax+a+3知f(0)=a+3,f(1)=4,又存在∃x0∈R,使得f(x0)<0,
知△=a2﹣4(a+3)>0即a<﹣2或a>6,
另g(x)=ax﹣2a,中恒过(2,0),
当a=0时,f(x)=x2﹣ax+a+3恒大于0,显然不成立.
若a>0时,g(x)=ax﹣2a<2,
∴a>0f(2)<0,则a>7,
若a<0时,g(x)=ax﹣2a>2,
此时函数f(x)=x2﹣ax+a+3图象的对称x=a2<-1,故函数在区间(a2,+∞),为增函数,
又f(1)=4,f(x0)<0不成立.
故选:A.
相关学案
这是一份(新高考)高考数学一轮复习题型归纳学案专题04《不等式》(解析版),共17页。学案主要包含了均值不等式的常见变形等内容,欢迎下载使用。
这是一份专题13直线方程 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共13页。
这是一份专题13椭圆 题型归纳讲义-2022届高三数学一轮复习(解析版)学案,共21页。












