高考数学一轮复习第七章第四节直线平面平行的判定及其性质课时作业理含解析北师大版

这是一份高考数学一轮复习第七章第四节直线平面平行的判定及其性质课时作业理含解析北师大版，共6页。
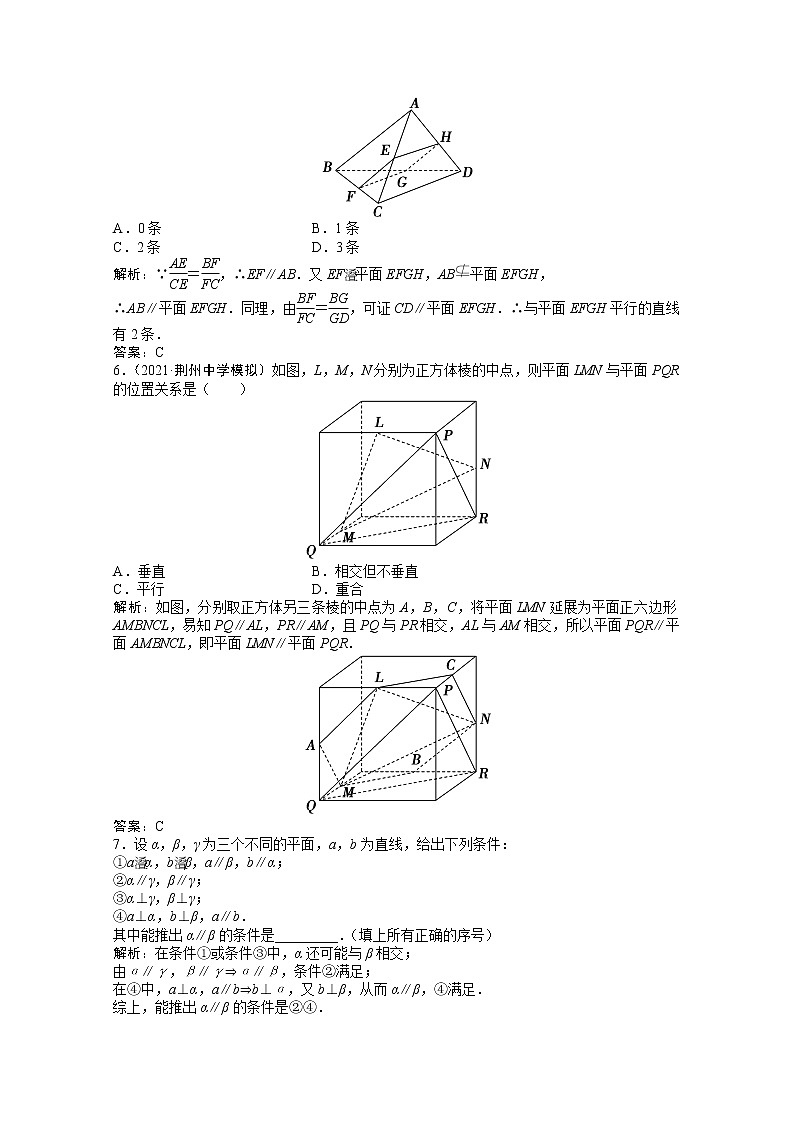
第四节 直线、平面平行的判定及其性质授课提示：对应学生用书第345页[A组　基础保分练]1．已知直线l和平面α，若l∥α，P∈α，则过点P且平行于l的直线（　　）A．只有一条，不在平面α内B．只有一条，且在平面α内C．有无数条，一定在平面α内D．有无数条，不一定在平面α内解析：过直线外一点作该直线的平行直线有且只有一条，因为点P在平面α内，所以这条直线也应该在平面α内．答案：B2．（2021·长沙模拟）已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是（　　）A．m∥α，n∥α，则m∥nB．m∥n，m∥α，则n∥αC．m⊥α，m⊥β，则α∥βD．α⊥γ，β⊥γ，则α∥β解析：对于A，平行于同一平面的两条直线可能相交，可能平行，也可能异面，故A不正确；对于B，m∥n，m∥α，则n∥α或nα，故B不正确；对于C，利用垂直于同一直线的两个平面平行，可知C正确；对于D，因为垂直于同一平面的两个平面的位置关系是相交或平行，故D不正确．答案：C3．已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是（　　）A．若α，β垂直于同一平面，则α与β平行B．若m，n平行于同一平面，则m与n平行C．若α，β不平行，则在α内不存在与β平行的直线D．若m，n不平行，则m与n不可能垂直于同一平面解析：由于α，β垂直于同一平面，则α与β平行或相交，利用正方体可判断，故A不正确；若m，n平行于同一平面，则m与n可能平行、相交或异面，故B不正确；利用正方体中的侧面与底面，侧面的上底面的棱与下底面的棱，能够找到平行线，所以C不正确；D正确．答案：D4．（2021·绍兴一中模拟）对于空间中的两条直线m，n和一个平面α，下列命题中为真命题的是（　　）A．若m∥α，n∥α，则m∥nB．若m∥α，nα，则m∥nC．若m∥α，n⊥α，则m∥nD．若m⊥α，n⊥α，则m∥n解析：对于A，直线m，n可能平行、异面或相交，故A错误；对于B，直线m，n可能平行，也可能异面，故B错误；对于C，m与n垂直而非平行，故C错误；对于D，垂直于同一平面的两直线平行，故D正确．答案：D5．如图，四边形EFGH为四面体ABCD的一个截面，若＝＝，则与平面EFGH平行的直线有（　　）A．0条　　　　　　　 B．1条C．2条  D．3条解析：∵＝，∴EF∥AB．又EF平面EFGH，AB平面EFGH，∴AB∥平面EFGH．同理，由＝，可证CD∥平面EFGH．∴与平面EFGH平行的直线有2条．答案：C6．（2021·荆州中学模拟）如图，L，M，N分别为正方体棱的中点，则平面LMN与平面PQR的位置关系是（　　）A．垂直  B．相交但不垂直C．平行  D．重合解析：如图，分别取正方体另三条棱的中点为A，B，C，将平面LMN延展为平面正六边形AMBNCL，易知PQ∥AL，PR∥AM，且PQ与PR相交，AL与AM相交，所以平面PQR∥平面AMBNCL，即平面LMN∥平面PQR．答案：C7．设α，β，γ为三个不同的平面，a，b为直线，给出下列条件：①aα，bβ，a∥β，b∥α；②α∥γ，β∥γ；③α⊥γ，β⊥γ；④a⊥α，b⊥β，a∥b．其中能推出α∥β的条件是_________．（填上所有正确的序号）解析：在条件①或条件③中，α还可能与β相交；由α∥γ，β∥γ⇒α∥β，条件②满足；在④中，a⊥α，a∥b⇒b⊥α，又b⊥β，从而α∥β，④满足．综上，能推出α∥β的条件是②④．答案：②④8．在正四棱柱ABCD­A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则点Q满足条件　　　　时，有平面D1BQ∥平面PAO．解析：如图所示，设Q为CC1的中点，因为P为DD1的中点，所以QB∥PA．又QB平面PAO，PA平面PAO，所以QB∥平面PAO．连接DB，因为P，O分别是DD1，DB的中点，所以D1B∥PO，又D1B平面PAO，PO平面PAO，所以D1B∥平面PAO．又D1B∩QB＝B，所以平面D1BQ∥平面PAO．故Q为CC1的中点时，有平面D1BQ∥平面PAO．答案：Q为CC1的中点9．（2021·唐山质检）如图，四边形ABCD与四边形ADEF都为平行四边形，M，N，G分别是AB，AD，EF的中点．求证：（1）BE∥平面DMF；（2）平面BDE∥平面MNG．证明：（1）设DF与GN交于点O，连接AE，则AE必过点O，且O为AE的中点，连接MO（图略），则MO为△ABE的中位线，所以BE∥MO．因为BE平面DMF，MO平面DMF，所以BE∥平面DMF．（2）因为N，G分别为AD，EF的中点，四边形ADEF为平行四边形，所以DE∥GN．因为DE平面MNG，GN平面MNG，所以DE∥平面MNG．因为M为AB的中点，N为AD的中点，所以MN为△ABD的中位线，所以BD∥MN．因为BD平面MNG，MN平面MNG，所以BD∥平面MNG．因为DE∩BD＝D，BD，DE平面BDE，所以平面BDE∥平面MNG．10．（2021·南昌模拟）如图所示，在四棱锥P­ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，PA＝2，AB＝1．设M，N分别为PD，AD的中点．（1）求证：平面CMN∥平面PAB；（2）求三棱锥P­ABM的体积．解析：（1）证明：因为M，N分别为PD，AD的中点，所以MN∥PA．又因为MN平面PAB，PA平面PAB，所以MN∥平面PAB．在Rt△ACD中，∠CAD＝60°，CN是Rt△ACD中斜边上的中线，所以CN＝AN，所以∠ACN＝60°．又因为∠BAC＝60°，所以CN∥AB．因为CN平面PAB，AB平面PAB，所以CN∥平面PAB．又因为CN∩MN＝N，所以平面CMN∥平面PAB．（2）由（1）知，平面CMN∥平面PAB，所以MC∥平面PAB，所以点M到平面PAB的距离等于点C到平面PAB的距离．由AB＝1，∠ABC＝90°，∠BAC＝60°，得BC＝，所以VP­ABM＝VM­PAB＝VC­PAB＝VP­ABC＝××1××2＝．[B组　能力提升练]1．如图，平面PAD⊥平面ABCD，∠ABC＝∠BCD＝90°，PA＝PD＝AD＝AB＝2CD＝2，H为PB的中点．（1）求证：CH∥平面PAD；（2）求点C到平面PAB的距离．解析：（1）证明：取PA的中点E，连接HE，DE（图略），则EH綊AB．∵∠ABC＝∠BCD＝90°，∴AB∥CD．又AB＝2CD，∴CD綊AB，∴EH綊CD，四边形CDEH为平行四边形，∴CH∥DE，又DE平面PAD，CH平面PAD，∴CH∥平面PAD．（2）取AD的中点F，连接PF，FB，AH（图略），则∠PFB＝90°，PF＝，BF＝，PB＝，AH＝，∴S△PAB＝××＝，连接AC，则V三棱锥C­PAB＝V三棱锥P­ABC，设点C到平面PAB的距离为h，∴××h＝××2××，∴h＝＝．∴点C到平面PAB的距离为．2．（2021·南通模拟）如图所示，斜三棱柱ABC­A1B1C1中，点D，D1分别为AC，A1C1上的点．（1）当等于何值时，BC1∥平面AB1D1？（2）若平面BC1D∥平面AB1D1，求的值．解析：（1）如图所示，取D1为线段A1C1的中点，此时＝1．连接A1B，交AB1于点O，连接OD1．由棱柱的性质知，四边形A1ABB1为平行四边形，∴点O为A1B的中点．在△A1BC1中，点O，D1分别为A1B，A1C1的中点，∴OD1∥BC1．又∵OD1平面AB1D1，BC1平面AB1D1，∴BC1∥平面AB1D1．∴当＝1时，BC1∥平面AB1D1．（2）由平面BC1D∥平面AB1D1，且平面A1BC1∩平面BC1D＝BC1，平面A1BC1∩平面AB1D1＝D1O，得BC1∥D1O，∴＝，又由题（1）可知＝，＝1，∴＝1，即＝1．[C组　创新应用练]1．如图，在长方体ABCD­A1B1C1D1中，AA1＝6，AB＝3，AD＝8，点M是棱AD的中点，点N在棱AA1上，且满足AN＝2NA1，P是侧面四边形ADD1A1内一动点（含边界），若C1P∥平面CMN，则线段C1P长度的最小值是_________．解析：取A1D1的中点Q，过点Q在平面ADD1A1内作MN的平行线交DD1于点E，易知平面C1QE∥平面CMN，在△C1QE中作C1P⊥QE（图略），此时C1P取得最小值．答案：2．在如图所示的一块木料中，棱BC平行于平面A′B′C′D′．（1）要经过平面A′B′C′D′内的一点P和棱BC将木料锯开，应怎样画线？（2）所画的线与平面ABCD是什么位置关系？并证明你的结论．解析：（1）过点P作B′C′的平行线，交A′B′，C′D′于点E，F，连接BE，CF．作图如下：（2）EF∥平面ABCD．理由如下：因为BC∥平面A′B′C′D′，又因为平面B′C′CB∩平面A′B′C′D′＝B′C′，所以BC∥B′C′，因为EF∥B′C′，所以EF∥BC，又因为EF平面ABCD，BC平面ABCD，所以EF∥平面ABCD．