高中数学人教版新课标B选修1-13.3.2利用导数研究函数的极值课前预习ppt课件

这是一份高中数学人教版新课标B选修1-13.3.2利用导数研究函数的极值课前预习ppt课件，共30页。PPT课件主要包含了极值点，端点处，最大值，最小值，解析答案，反思与感悟，解后反思，分类讨论思想的应用，解得0＜a＜e，－71等内容，欢迎下载使用。

知识梳理 自主学习
题型探究 重点突破
当堂检测 自查自纠
知识梳理 自主学习
知识点一　函数f(x)在闭区间[a，b]上的最值函数f(x)在闭区间[a，b]上的图象是一条连续不断的曲线，则该函数在[a，b]上一定能够取得最大值与最小值，函数的最值必在 处或 处取得.知识点二　求函数y＝f(x)在[a，b]上的最值的步骤(1)求函数y＝f(x)在(a，b)内的 .(2)将函数y＝f(x)的各极值与 的函数值f(a)，f(b)比较，其中最大的一个是 ，最小的一个是 .
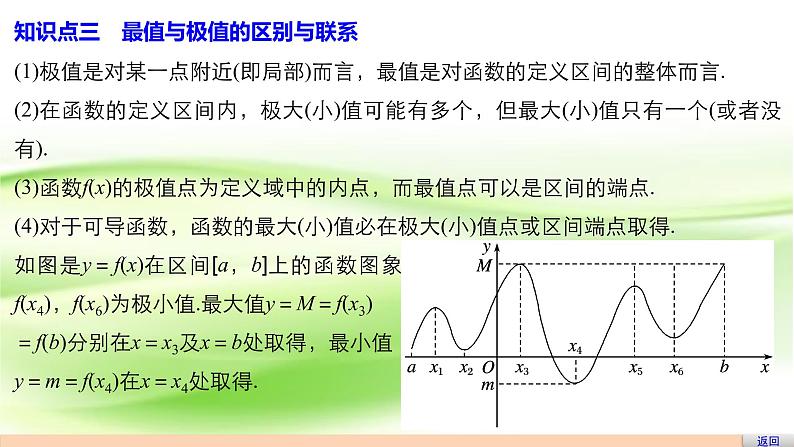
知识点三　最值与极值的区别与联系(1)极值是对某一点附近(即局部)而言，最值是对函数的定义区间的整体而言.(2)在函数的定义区间内，极大(小)值可能有多个，但最大(小)值只有一个(或者没有).(3)函数f(x)的极值点为定义域中的内点，而最值点可以是区间的端点.(4)对于可导函数，函数的最大(小)值必在极大(小)值点或区间端点取得.如图是y＝f(x)在区间[a，b]上的函数图象.显然f(x1)，f(x3)，f(x5)为极大值，f(x2)，f(x4)，f(x6)为极小值.最大值y＝M＝f(x3)＝f(b)分别在x＝x3及x＝b处取得，最小值y＝m＝f(x4)在x＝x4处取得.
题型探究 重点突破
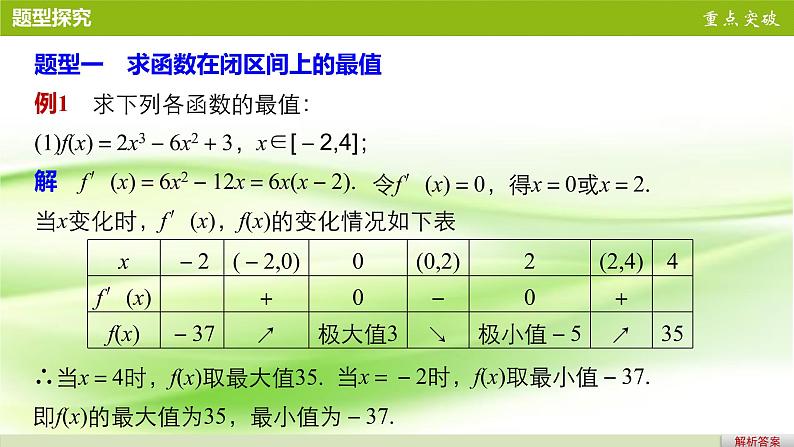
题型一　求函数在闭区间上的最值例1　求下列各函数的最值：(1)f(x)＝2x3－6x2＋3，x∈[－2,4]；解　f′(x)＝6x2－12x＝6x(x－2).当x变化时，f′(x)，f(x)的变化情况如下表
令f′(x)＝0，得x＝0或x＝2.
∴当x＝4时，f(x)取最大值35.即f(x)的最大值为35，最小值为－37.
当x＝－2时，f(x)取最小值－37.
(2)f(x)＝x3－3x2＋6x－2，x∈[－1,1].解　f′(x)＝3x2－6x＋6＝3(x2－2x＋2)＝3(x－1)2＋3，∵f′(x)在[－1,1]内恒大于0，∴f′(x)在[－1,1]上为增函数.故x＝－1时，f(x)最小值＝－12；x＝1时，f(x)最大值＝2.即f(x)的最小值为－12，最大值为2.
(1)求函数的最值，显然求极值是关键的一步.但仅仅是求最值，可用下面简化的方法求得.①求出导数为零的点.②比较这些点与端点处函数值的大小，就可求出函数的最大值和最小值.(2)若函数在闭区间[a，b]上连续且单调，则最大、最小值在端点处取得.
跟踪训练1　求下列函数的最值：
当x变化时，f′(x)，f(x)的变化情况如下表：
所以当x＝0时，f(x)有最小值f(0)＝0；即f(x)的最小值为0，最大值为π.
当x＝2π时，f(x)有最大值f(2π)＝π.
(2)f(x)＝e－x－ex，x∈[0，a]，a为正实数.
当x∈[0，a]时，f′(x)＜0恒成立，即f(x)在[0，a]上是减函数.故当x＝a时，f(x)有最小值f(a)＝e－a－ea；当x＝0时，f(x)有最大值f(0)＝e－0－e0＝0.即f(x)的最小值为e－a－ea，最大值为0.
题型二　含参数的函数的最值问题例2　已知函数f(x)＝－x3＋3x2＋9x＋a.(1)求f(x)的单调递减区间；解　f′(x)＝－3x2＋6x＋9＝－3(x＋1)(x－3).令f′(x)＜0，得x＜－1或x＞3，故函数f(x)的单调递减区间为(－∞，－1)，(3，＋∞).
(2)若f(x)在区间[－2,2]上的最大值为20，求它在该区间上的最小值.解　因为f(－2)＝8＋12－18＋a＝2＋a，所以f(2)＞f(－2)，所以f(x)在[－1,2]上单调递增，所以f(－1)是f(x)的极小值，且f(－1)＝a－5，所以f(2)和f(－1)分别是f(x)在区间[－2,2]上的最大值和最小值，于是有22＋a＝20，解得a＝－2.所以f(－1)＝－2－5＝－7，即函数f(x)在区间[－2,2]上的最小值为－7.
f(2)＝－8＋12＋18＋a＝22＋a，
因为在(－1,3)上f′(x)＞0，
函数的最值与极值及单调性密切相关，因而在求解函数的最值的问题时，一般都要判断函数的单调性与极值点.导数是研究函数与极值的有力工具.
跟踪训练2　已知函数f(x)＝ax3－6ax2＋b在[－1,2]上有最大值3，最小值－29，求a，b的值.
解　由题意，知a≠0.所以令f′(x)＝0，得x＝0或x＝4(舍去).若a＞0，当x变化时，f′(x)，f(x)的变化情况如下表：
由上表，知当x＝0时，f(x)取得最大值，又因为f(2)＝－16a＋3，f(－1)＝－7a＋3，故f(－1)＞f(2)，所以当x＝2时，f(x)取得最小值，即－16a＋3＝－29，解得a＝2.
所以f(0)＝b＝3，
因为f′(x)＝3ax2－12ax＝3ax(x－4)，x∈[－1,2]，
若a＜0，当x变化时，f′(x)，f(x)的变化情况如下表：
所以当x＝0时，f(x)取得最小值，所以f(0)＝b＝－29.又因为f(2)＝－16a－29，f(－1)＝－7a－29，所以当x＝2时，f(x)取得最大值，即－16a－29＝3，解得a＝－2.
故f(2)＞f(－1).
题型三　函数最值的应用例3　设函数f(x)＝tx2＋2t2x＋t－1(x∈R，t＞0).(1)求f(x)的最小值h(t)；解　∵f(x)＝t(x＋t)2－t3＋t－1(x∈R，t＞0)，∴当x＝－t时，f(x)取最小值f(－t)＝－t3＋t－1，即h(t)＝－t3＋t－1.
(2)若h(t)＜－2t＋m对t∈(0,2)恒成立，求实数m的取值范围.解　令g(t)＝h(t)－(－2t＋m)＝－t3＋3t－1－m，由g′(t)＝－3t2＋3＝0得t＝1，t＝－1(不合题意，舍去).当t变化时g′(t)、g(t)的变化情况如下表：
∴对t∈(0,2)，当t＝1时，g(t)max＝1－m，也就是g(t)<0对t∈(0,2)恒成立，故实数m的取值范围是(1，＋∞).
h(t)<－2t－m对t∈(0,2)恒成立，
只需g(t)max＝1－m<0，∴m>1.
(1)“恒成立”问题向最值问题转化是一种常见的题型，一般地，可采用分离参数法进行转化.λ≥f(x)恒成立⇔λ≥[f(x)]max；λ≤f(x)恒成立⇔λ≤[f(x)]min.对于不能分离参数的恒成立问题，直接求含参函数的最值即可.(2)此类问题特别要小心“最值能否取得到”和“不等式中是否含等号”的情况，以此来确定参数的范围能否取得“＝”.
跟踪训练3　已知函数f(x)＝ax4ln x＋bx4－c(x＞0)在x＝1处取得极值－3－c，其中a，b，c为常数，若对任意x＞0，不等式f(x)≥－2c2恒成立，求c的取值范围.解　由题意，知f(1)＝－3－c.
因此b－c＝－3－c，从而b＝－3.
由题意，知f′(1)＝0，即a－12＝0，得a＝12.所以f′(x)＝48x3ln x(x＞0)，当0＜x＜1时，f′(x)＜0，此时f(x)为减函数；当x＞1时，f′(x)＞0，此时f(x)为增函数.所以f(x)在x＝1处取得极小值f(1)＝－3－c，所以要使f(x)≥－2c2(x＞0)恒成立，
令f′(x)＝0，得x＝1.
并且此极小值也是最小值.
只需－3－c≥－2c2即可.
分析　(1)求出g(x)的表达式是解题的关键；(2)构造辅助函数，结合单调性求解；(3)显然g(x)的最值决定了参数a的取值范围.
当x∈(0,1)时，g′(x)＜0，故g(x)的单调递减区间是(0,1)，单调递增区间是(1，＋∞).因此，x＝1是g(x)的唯一极值点，且为极小值点，从而是最小值点，所以g(x)的最小值为g(1)＝1.
当x∈(1，＋∞)时，g′(x)＞0，
当x∈(0,1)∪(1，＋∞)时，h′(x)＜0，h′(1)＝0，因此，h(x)在(0，＋∞)内单调递减.
(3)由(1)，知g(x)的最小值为1.
1.函数f(x)＝－x2＋4x＋7，在x∈[3,5]上的最大值和最小值分别是(　　)A.f(2)，f(3) B.f(3)，f(5)C.f(2)，f(5) D.f(5)，f(3)解析　∵f′(x)＝－2x＋4，∴当x∈[3,5]时，f′(x)<0，故f(x)在[3,5]上单调递减，故f(x)的最大值和最小值分别是f(3)，f(5).
2.函数f(x)＝x3－3x(|x|<1)(　　)A.有最大值，但无最小值B.有最大值，也有最小值C.无最大值，但有最小值D.既无最大值，也无最小值解析　f′(x)＝3x2－3＝3(x＋1)(x－1)，当x∈(－1,1)时，f′(x)<0，所以f(x)在(－1,1)上是单调递减函数，无最大值和最小值，故选D.
解析　因为y′＝1－cs x，
所以y的最大值为ymax＝π－sin π＝π，故选C.
4.函数f(x)＝x3－3x2－9x＋k在区间[－4,4]上的最大值为10，则其最小值为________.解析　f′(x)＝3x2－6x－9＝3(x－3)(x＋1).由f′(x)＝0得x＝3或x＝－1.又f(－4)＝k－76，f(3)＝k－27，f(－1)＝k＋5，f(4)＝k－20.由f(x)max＝k＋5＝10，得k＝5，∴f(x)min＝k－76＝－71.
5.已知a为实数，f(x)＝(x2－4)(x－a)，若f′(－1)＝0，函数f(x)在[－2,2]上的最大值为___，最小值为_____.解析　由原式，得f(x)＝x3－ax2－4x＋4a，f′(x)＝3x2－2ax－4.
f′(x)＝3x2－x－4.