广东省2021-2022学年高三上学期综合能力测试数学试题

这是一份广东省2021-2022学年高三上学期综合能力测试数学试题，共9页。
1．答卷前，考生要务必填涂答题卷上的有关项目．
2．选择题每小题选出答案后，用2B铅笔把答案涂在答题卷相应的位置上．
3．非选择题必须用黑色字迹的钢笔或签字管作答，案必须写在答题卷各题目指定区域内：如需改动，先划掉原来的答案，然后再写上新的答案：不准使用铅笔和涂改液，不按以上要求作答的答案无效．
4．请考生保持答题卷的整洁，考试结束后，将答题卷交回．
一、选择题本题共8小题每小题5分共40分在每小题给出的四个选项中只有一项是符合题目要求的．
1. 已知集合，，则（ ）
A. B. C. D.
【答案】D
2. 复数（i为虚数单位）的共轭复数（ ）
A B. C. D.
【答案】D
3. 若抛物线上的点到焦点的距离是4，则抛物线的方程为（ ）
A. B.
C. D.
【答案】B
4. 基本分裂数m，是一个衡量细菌分裂的参数，简单来说在1小时内1个细菌平均可以分裂成m个细菌．已知在某种细菌培养过程中，原有细菌26个，经过了3小时后细菌增至105个，那么，参考上述数据预计再经过（ ）小时细菌就会突破十万个．
A. 12B. 15C. 18D. 21
【答案】B
5. 已知为三角形的内角，且，则（ ）
A. B. C. D.
【答案】A
6. 受全球新冠疫情影响，2020东京奥运会延期至2021年7月23日到8月8日举行，某射箭选手积极备战奥运，在临赛前的一次训练中共射了1组共72支箭，下表是命中环数的部分统计信息
已知该次训练的平均环数为9.125环，据此水平，正式比赛时射出的第一支箭命中黄圈（不小于9环）的概率约为（ ）
A 0.31B. 0.65C. 0.86D. 1
【答案】C
7. 如图，直线依次与曲线、及x轴相交于点A、点B及点C，若B是线段的中点，则（ ）
A. B.
C. D.
【答案】B
8. 已知函数（其中且），若当时，恒有，则a的取值范围是（ ）
A. B.
C. D.
【答案】D
二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求全部选对的得5分，有选错的得0分，部分选对的得2分．
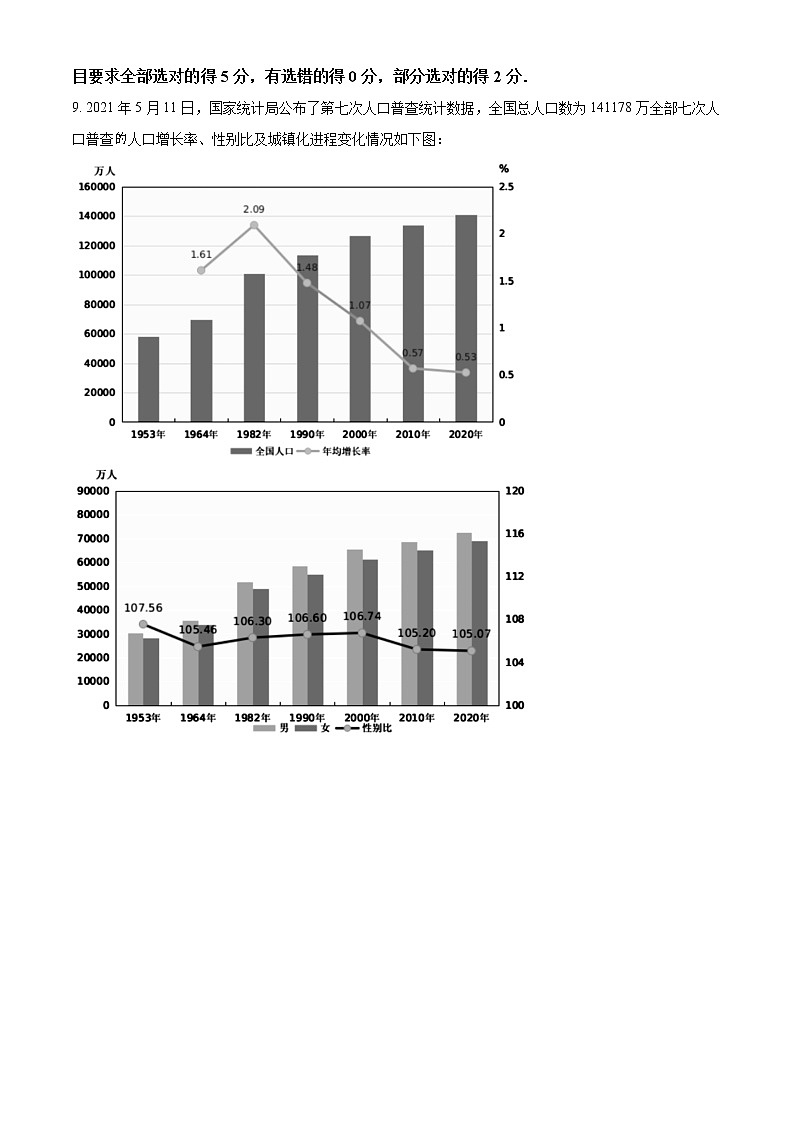
9. 2021年5月11日，国家统计局公布了第七次人口普查统计数据，全国总人口数为141178万全部七次人口普查人口增长率、性别比及城镇化进程变化情况如下图：
根据以上信息，下列统计结论正确的是（ ）
A. 七次人口普查的人口增长率逐次减少
B. 七次人口普查的性别比趋于稳定，重男轻女的传统观念有所转变
C. 七次人口普查的城镇人口比重逐次提高
D. 第七次人口普查城镇人口數与乡村人口数相差超过4亿
【答案】BC
10. 已知函数，则（ ）
A.
B. 是上的减函数
C. 的值域为
D. 不等式的解集为
【答案】ABD
11. 已知函数的部分图象如图所示，下列说法正确的是（ ）
A. 函数的图象关于点对称
B. 函数的图象关于直线对称
C. 函数在单调递减
D. 该图象向右平移个单位可得的图象
【答案】ABD
12. 下列不等式成立的是（ ）
A. B.
C. D.
【答案】AC
三、填空题：本题共4小题，每小题5分，共20分，其中第10题第一空2分，第二空3分．
13. 已知的展开式的二项式系数之和为16，则各项系数之和为__________．（用数字作答）
【答案】81
14. 若椭圆的左顶点、上顶点以及右焦点构成直角三角形，则该椭圆的离心率为__________．
【答案】
15. 直三棱柱的所有顶点都在球O的球面上，，，，，则球O的体积是__________．
【答案】
16. 定义在上的函数，若是奇函数，则__________；满足的的取值范围是_______．
【答案】 ①. ②.
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17. 已知的内角，，的对边分别为，，，且．
（1）求；
（2）若，且，求的面积．
【答案】（1）；（2）.
18. 已知各项均为正数的数列满足，．
（1）求的通项公式；
（2）若求数列的前n项和．
【答案】（1）；（2）.
19. 如图，长方体中，，在棱上且，在平面内过点作直线，使得．
（1）在图中画出直线并说明理由；
（2）若，求直线与平面所成角正弦值．
【答案】（1）答案见解析；（2）.
20. 研究表明，子女的平均身高与父母的平均身高有较强的线性相关性．某数学小组收集到8个家庭的相关数据，下面是小组制作的统计图散点图、回归直线及回归方程）与原始数据表（局部缺失）：
（1）表中8号家庭的子女平均身高数据缺失，试根据统计学知识找回该数据：
（2）由图中观察到4号家庭的数据点明显偏离回归直线l，试计算其残差（残差=观测值-预报值）
若剔除4号家庭数据点后，用余下的7个散点作线性回归分析，得到新的回归直线，判断并证明l与的位置关系．
附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为：，．
【答案】（1）188；（2）平行，证明见解析.
21. 已知双曲线的右焦点为，一条渐近线方程为．
（1）求双曲线的方程；
（2）记的左、右顶点分别为，过的直线交的右支于两点，连结交直线于点，求证：三点共线．
【答案】（1）；（2）证明见解析.
22. 已知函数，．
（1）确定a的所有值，使函数是上的增函数；
（2）若函数在和处取得极小值和，证明：．
【答案】（1）；（2）证明见解析.
环数
7
8
9
10
频数
0
3
a
b
22
家庭编号
1
2
3
4
5
6
7
8
父母平均身高（）
160.5
165
167
170
170.5
173
174
180
子女平均身高（）
168
170
172.5
187
1745
176
180
*