2022届高考数学一轮复习第七章立体几何7.7立体几何中的向量方法学案理含解析北师大版

第七节　立体几何中的向量方法

授课提示：对应学生用书第158页

知识点　空间角的求法

1．设直线l，m的方向向量分别为a，b，平面α，β的法向量分别为u，ν，则

（1）线线平行：l∥m⇔a∥b⇔a＝kb，k∈R；

线面平行：l∥α⇔a⊥u⇔a·u＝0；

面面平行：α∥β⇔u∥ν⇔u＝kν，k∈RＷ．

（2）线线垂直：l⊥m⇔a⊥b⇔a·b＝0；

线面垂直：l⊥α⇔a∥u⇔a＝ku，k∈R；

面面垂直：α⊥β⇔u⊥ν⇔u·ν＝0Ｗ．

2．空间角的求法

（1）异面直线所成的角

设a，b分别是两异面直线l1，l2的方向向量，则

（2）求直线与平面所成的角

设直线l的方向向量为a，平面α的法向量为n，直线l与平面α所成的角为θ，则sin θ＝|cos〈a，n〉|＝．

（3）求二面角的大小

①如图a，AB，CD是二面角α­l­β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈，〉．

②如图bc，n1，n2分别是二面角α­l­β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos〈n1，n2〉|，二面角的平面角大小是向量n1与n2的夹角（或其补角）．

• 温馨提醒 •

利用空间向量法求二面角时易忽视判断二面角大小，从而致误．解题时注意结合图形判断二面角的平面角是锐角还是钝角，从而在下结论时作出正确判断．

1．已知两平面的法向量分别为m＝（0，1，0），n＝（0，1，1），则两平面所成的二面角的大小为_________．

解析：cos〈m，n〉＝＝＝，即〈m，n〉＝45°，所以两平面所成二面角为45°或180°－45°＝135°．

答案：45°或135°

2．在正方体ABCD­A1B1C1D1中，E是C1D1的中点，则异面直线DE与AC夹角的余弦值为_________．

解析：如图建立空间直角坐标系D­xyz，设DA＝1，A（1，0，0），C（0，1，0），E，则＝（－1，1，0），＝，设异面直线DE与AC所成的角为θ，则cos θ＝|cos〈，〉|＝．

答案：

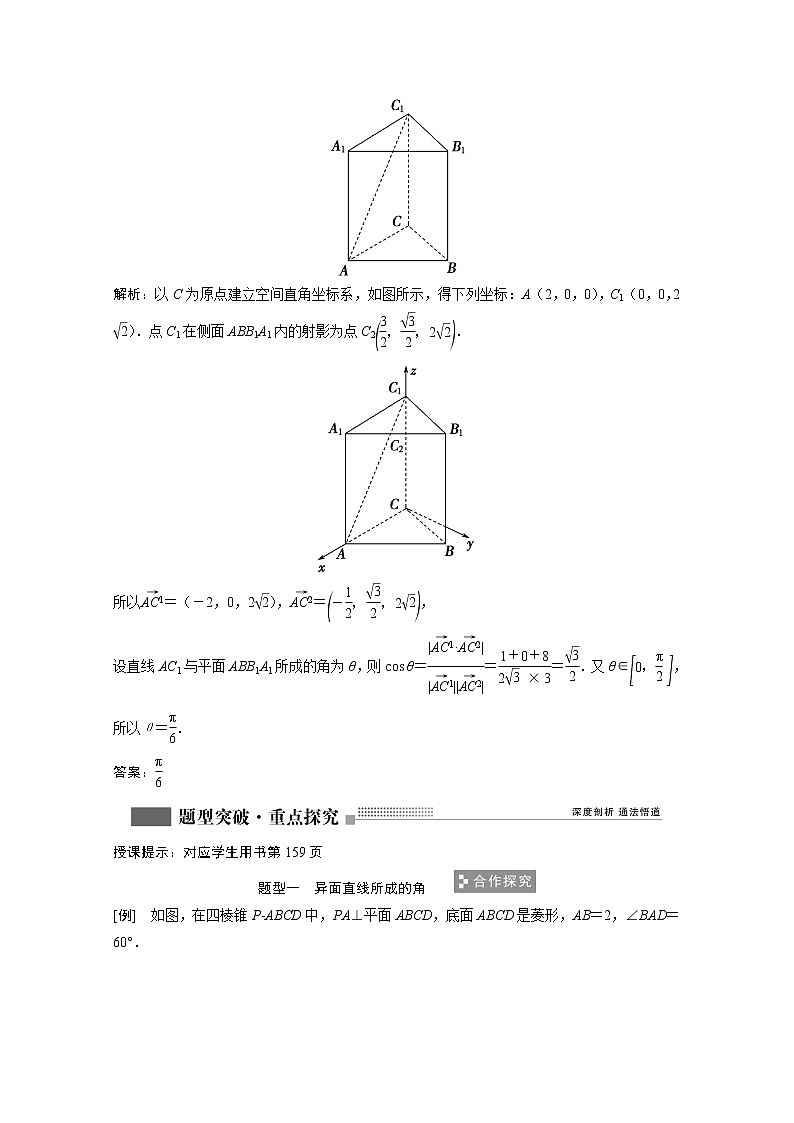
3．正三棱柱（底面是正三角形的直棱柱）ABC­A1B1C1的底面边长为2，侧棱长为2，则AC1与侧面ABB1A1所成的角为_________．

解析：以C为原点建立空间直角坐标系，如图所示，得下列坐标：A（2，0，0），C1（0，0，2）．点C1在侧面ABB1A1内的射影为点C2．

所以＝（－2，0，2），＝，

设直线AC1与平面ABB1A1所成的角为θ，则cos θ＝＝＝．又θ∈，所以θ＝．

答案：

授课提示：对应学生用书第159页

题型一　异面直线所成的角　　

[例]　如图，在四棱锥P­ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB＝2，∠BAD＝60°．

（1）求证：BD⊥平面PAC；

（2）若PA＝AB，求PB与AC所成角的余弦值．

[解析]　（1）证明：因为四边形ABCD是菱形，

所以AC⊥BD．

因为PA⊥平面ABCD，所以PA⊥BD．

又因为AC∩PA＝A，所以BD⊥平面PAC．

（2）设AC∩BD＝O．

因为∠BAD＝60°，PA＝AB＝2，

所以BO＝1，AO＝CO＝．

如图，以O为坐标原点，建立空间直角坐标系O­xyz，则P（0，－，2），A（0，－，0），B（1，0，0），C（0，，0）．

所以＝（1，，－2），＝（0，2，0）．

设PB与AC所成角为θ，则

cos θ＝＝＝．

即PB与AC所成角的余弦值为．

向量法求异面直线所成角的两种方法及一个注意点

（1）两种方法：

①基向量法：利用线性运算．

②坐标法：利用坐标运算．

（2）一个注意点：

注意向量法求异面直线所成角与向量夹角的区别，尤其是取值范围．

[对点训练]

如图，S是正三角形ABC所在平面外一点，M，N分别是AB和SC的中点，SA＝SB＝SC，且∠ASB＝∠BSC＝∠CSA＝90°，则异面直线SM与BN所成角的余弦值为（　　）

A．－　　　　　　 B．

C．－  D．

解析：不妨设SA＝SB＝SC＝1，以S为坐标原点，SA，SB，SC所在直线分别为x轴，y轴，z轴建立空间直角坐标系S­xyz（图略），则A（1，0，0），B（0，1，0），C（0，0，1），S（0，0，0），则M，N，所以＝，＝，所以||＝，||＝，·＝－，所以cos〈，〉＝＝－，所以异面直线SM与BN所成角的余弦值为．

答案：B

题型二　直线与平面所成的角　　

[例]　如图，在直三棱柱ABC­A1B1C1中，AB＝2，AC＝1，CC1＝，∠ABC＝30°，D为AB的中点．

（1）证明：AC1∥平面B1CD；

（2）求直线DC1与平面B1CD所成角的正弦值．

[解析]　（1）证明：连接BC1交B1C于点E，连接DE，因为四边形BB1C1C是矩形，所以点E是BC1的中点，

又点D为AB的中点，

所以DE是△ABC1的中位线，

所以DE∥AC1．

因为DE⊂平面B1CD，AC1⊄平面B1CD，

所以AC1∥平面B1CD．

（2）由AB＝2，AC＝1，∠ABC＝30°，可得AC⊥BC，

分别以CA，CB，CC1所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系C­xyz，

则C（0，0，0），B1（0，，），D，C1（0，0，），

所以＝，＝（0，，），

＝．

设直线DC1与平面B1CD所成角为θ，平面B1CD的法向量为m＝（x，y，z），

则即

令z＝1，得m＝（，－1，1），

所以sin θ＝|cos〈m，〉|＝＝＝．

利用平面的法向量求线面角的两个注意点

（1）求出直线的方向向量与平面的法向量所夹的锐角（钝角时取其补角），取其余角即为所求．

（2）若求线面角的余弦值，要注意利用平方关系sin2θ＋cos2θ＝1求出其值．不要误认为直线的方向向量与平面的法向量所夹角的余弦值即为所求．

[对点训练]

（2021·东北三校模拟）在正三棱柱ABC­A1B1C1中，已知AB＝1，D在棱BB1上，且BD＝1，则AD与平面AA1C1C所成角的正弦值为（　　）

A．　　　　　　 B．－

C．  D．－

解析：取AC的中点E，连接BE，则BE⊥AC，以B为坐标原点，BE，BB1所在直线分别为x轴，z轴，建立如图所示的空间直角坐标系B­xyz，则A，D（0，0，1），B（0，0，0），E，

则＝，＝．

∵平面ABC⊥平面AA1C1C，平面ABC∩平面AA1C1C＝AC，BE⊥AC，BE⊂平面ABC，∴BE⊥平面AA1C1C，

∴＝为平面AA1C1C的一个法向量．

设AD与平面AA1C1C所成角为α，

∵cos〈，〉＝＝－，

∴sin α＝|cos〈，〉|＝．

答案：A

题型三　二面角　　

[例]　（2020·高考全国卷Ⅰ）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE＝AD．△ABC是底面的内接正三角形，P为DO上一点，PO＝DO．

（1）证明：PA⊥平面PBC；

（2）求二面角B­PC­E的余弦值．

解析：（1）证明：设DO＝a，由题设可得PO＝a，AO＝a，

AB＝AC＝BC＝a，PA＝PB＝PC＝a．

因此PA2＋PB2＝AB2，从而PA⊥PB．

又PA2＋PC2＝AC2，故PA⊥PC．所以PA⊥平面PBC．

（2）以O为坐标原点，的方向为y轴正方向，||为单位长度，建立如图所示的空间直角坐标系O­xyz．

由题设可得E（0，1，0），A（0，－1，0），C，P．

所以＝，

＝．

设m＝（x，y，z）是平面PCE的法向量，则

即

可取m＝．

由（1）知＝是平面PCB的一个法向量．

记n＝，则cos〈n，m〉＝＝．

所以二面角B­PC­E的余弦值为．

利用法向量求二面角时的两个注意点

（1）对于某些平面的法向量要注意题中条件隐含着，不用单独求．

（2）注意判断二面角的平面角是锐角还是钝角，可结合图形进行判断，以防结论失误．

[对点训练]

如图，在三棱柱ABC­A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC＝BC＝2，CC1＝3，点D，E分别在棱AA1和棱CC1上，且AD＝1，CE＝2，M为棱A1B1的中点．

（1）求证：C1M⊥B1D；

（2）求二面角B­B1E­D的正弦值；

（3）求直线AB与平面DB1E所成角的正弦值．

解析：依题意，以C为原点，分别以，，的方向为x轴、y轴、z轴的正方向建立空间直角坐标系（如图），

 可得C（0，0，0），A（2，0，0），B（0，2，0），C1（0，0，3），

A1（2，0，3），B1（0，2，3），D（2，0，1），E（0，0，2），M（1，1，3）．

（1）依题意，＝（1，1，0），＝（2，－2，－2），

从而·＝2－2＋0＝0，所以C1M⊥B1D；

（2）依题意，＝（2，0，0）是平面BB1E的一个法向量，

＝（0，2，1），＝（2，0，－1）．

设n＝（x，y，z）为平面DB1E的法向量，

则即

不妨设x＝1，可得n＝（1，－1，2）．

cos〈·n〉＝＝＝，

∴sin〈，n〉＝＝．

所以，二面角B­B1E­D的正弦值为；

（3）依题意，＝（－2，2，0）．

由（2）知n＝（1，－1，2）为平面DB1E的一个法向量，于是

cos〈，n〉＝＝＝－．

所以，直线AB与平面DB1E所成角的正弦值为．

　向量法中的核心素养

数学运算——利用空间向量求距离

[例]　如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB＝2，求点A到平面MBC的距离．

[解析]　如图，取CD的中点O，连接OB，OM，因为△BCD与△MCD均为正三角形，所以OB⊥CD，OM⊥CD，又平面MCD⊥平面BCD，平面MCD∩平面BCD＝CD，OM平面MCD，所以MO⊥平面BCD．

以O为坐标原点，直线OC，BO，OM分别为x轴，y轴，z轴，建立空间直角坐标系O­xyz．

因为△BCD与△MCD都是边长为2的正三角形，

所以OB＝OM＝，

则O（0，0，0），C（1，0，0），M（0，0，），

B（0，－，0），A（0，－，2），所以＝（1，，0）．

＝（0，，）．

设平面MBC的法向量为n＝（x，y，z），

由得

即

取x＝，可得平面MBC的一个法向量为n＝（，－1，1）．

又＝（0，0，2），

所以所求距离为d＝＝．

求解点到平面的距离可直接转化为求向量在平面的法向量上的射影的长．如图，设点P在平面α外，n为平面α的法向量，在平面α内任取一点Q，则点P到平面α的距离d＝．

[对点训练]

如图所示，在长方体ABCD­A1B1C1D1中，AD＝AA1＝1，AB＝2，点E在棱AB上移动．

（1）证明：D1E⊥A1D；

（2）当E为AB的中点时，求点E到平面ACD1的距离．

解析：以D为坐标原点，直线DA，DC，DD1所在直线分别为x轴，y轴，z轴建立空间直角坐标系（图略），设AE＝x，则D（0，0，0），A1（1，0，1），D1（0，0，1），E（1，x，0），A（1，0，0），C（0，2，0）．

（1）证明：＝（1，x，－1），＝（－1，0，－1），因为·＝0，所以D1E⊥A1D．

（2）因为E为AB的中点，则E（1，1，0），从而＝（1，1，－1），＝（－1，2，0），＝（－1，0，1），

设平面ACD1的法向量为n＝（a，b，c），则

即得从而可取n＝（2，1，2），所以点E到平面ACD1的距离h＝＝＝．