





数学必修 第一册第2章 常用逻辑用语2.2 充分条件、必要条件、冲要条件图文课件ppt
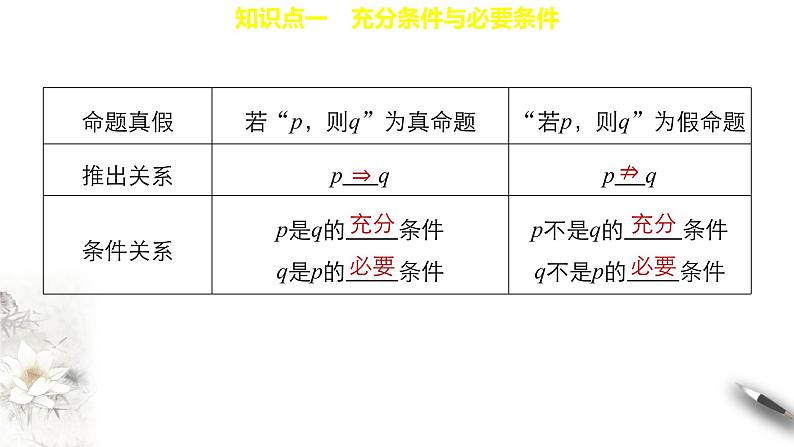
展开知识点一 充分条件与必要条件
知识点二 充要条件的概念
(1)定义:若p⇒q且q⇒p,则记作 ,此时p是q的充分必要条件,简称充要条件.(2)条件与结论的等价性:如果p是q的充要条件,那么q也是p的 .
例1 判断下列说法中,p是q的充分条件的是____.①p:“x=1”,q:“x2-2x+1=0”;②设a,b是实数,p:“a+b>0”,q:“ab>0”.
类型一 充分条件与必要条件的概念
解析 对①,p⇒q; ②p⇏q,故填①.
引申探究 例1中p是q的必要条件的是________.解析 ① x2-2x+1=0⇒x=1,即q⇒p; ② q⇏p.故填①.
变式 a>b的一个充分不必要条件是A.a2>b2 B.|a|>|b|C. D.a-b>1
解析 a-b>1⇒a-b>0而a-b>0⇏a-b>1,故选D.
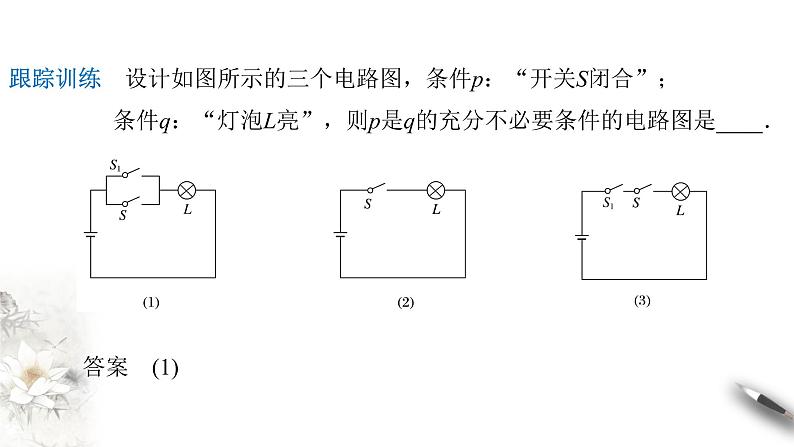
跟踪训练 设计如图所示的三个电路图,条件p:“开关S闭合”; 条件q:“灯泡L亮”,则p是q的充分不必要条件的电路图是____.
例1 (1)设x>0,y∈R,则“x>y”是“x>|y|”的A.充要条件 B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件
类型二 充要条件的判断
解析 分别判断x>y⇒x>|y|与x>|y|⇒x>y是否成立,从而得到答案.当x=1,y=-2时,x>y,但x>|y|不成立;若x>|y|,因为|y|≥y,所以x>y.所以x>y是x>|y|的必要不充分条件.
(2)下列所给的p,q中,p是q的充要条件的为_______.(填序号)①若a,b∈R,p:a2+b2=0,q:a=b=0;②p:|x|>3,q:x2>9.
解析 ①若a2+b2=0,则a=b=0,即p⇒q;若a=b=0,则a2+b2=0,即q⇒p,故p⇔q,所以p是q的充要条件.②由于p:|x|>3⇔q:x2>9,所以p是q的充要条件.
跟踪训练 (1)a,b中至少有一个不为零的充要条件是A.ab=0 B.ab>0C.a2+b2=0 D.a2+b2>0
解析 a2+b2>0,则a,b不同时为零;a,b中至少有一个不为零, 则a2+b2>0.
(2)设甲、乙、丙是三个命题,如果甲是乙的必要条件,丙是乙的充分条件但不是乙的必要条件,那么( )A.丙是甲的充分条件,但不是甲的必要条件B.丙是甲的必要条件,但不是甲的充分条件C.丙是甲的充要条件D.丙既不是甲的充分条件,也不是甲的必要条件
解析 因为甲是乙的必要条件,所以乙⇒甲.又因为丙是乙的充分条件,但不是乙的必要条件,所以丙⇒乙,但乙D⇏丙,如图.综上,有丙⇒甲,但甲D⇏丙,既丙是甲的充分条件,但不是甲的必要条件.
类型三 由条件关系求参数取值范围
例3 已知p:x<-2,q:x
变式 若“x2>1”是“x
例4 (1)“方程x2-2x-a=0无实根”的充要条件是______.
解析 方程x2-2x-a=0无实根,所以有Δ=4+4a<0,解得a<-1.反之,若a<-1,则Δ<0,方程x2-2x-a=0无实根.故“方程x2-2x-a=0无实根”的充要条件是a<-1.
(2)求证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
证明 充分性:∵ac<0,∴一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,∴方程一定有两个不等实根,设两实根为x1,x2,则x1x2= <0,∴方程的两根异号,即方程ax2+bx+c=0有一正根和一负根.必要性:∵方程ax2+bx+c=0有一正根和一负根,设两实根为x1,x2,则由根与系数的关系得x1x2= <0,且Δ=b2-4ac>0,即ac<0.综上可知,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
又由x>y,得y-x<0,所以xy>0.
(2)充分性:由xy>0及x>y,
1.“x>0”是“x≠0”的A.充分不必要条件 B.必要不充分条件C.充分条件 D.既不充分也不必要条件
解析 ∵x>0⇒x≠0,而x≠0⇏x>0,∴x>0是x≠0的充分不必要条件.
2.若a∈R,则“a=1”是“|a|=1”的A.充分条件B.必要条件C.既不是充分条件也不是必要条件D.无法判断
解析 当a=1时,|a|=1成立,但|a|=1时,a=±1,所以a=1不一定成立.∴“a=1”是“|a|=1”的充分条件.
3.从“充分条件”“必要条件”中选出适当的一种填空:(1)“ax2+bx+c=0(a≠0)有实根”是“ac<0”的_________.(2)“△ABC≌△A′B′C′”是“△ABC∽△A′B′C′”的_________.
4.“x2>2 017”是“x2>2 016”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
5.a<0,b<0的一个必要条件为A.a+b<0 B.a+b>0
解析 a+b<0⇏a<0,b<0,而a<0,b<0⇒a+b<0.
高中数学苏教版 (2019)必修 第一册第2章 常用逻辑用语2.2 充分条件、必要条件、冲要条件教案配套ppt课件: 这是一份高中数学苏教版 (2019)必修 第一册第2章 常用逻辑用语2.2 充分条件、必要条件、冲要条件教案配套ppt课件,共23页。PPT课件主要包含了随堂小测,必要不充分,充分不必要等内容,欢迎下载使用。
高中人教A版 (2019)1.4 充分条件与必要条件教案配套课件ppt: 这是一份高中人教A版 (2019)1.4 充分条件与必要条件教案配套课件ppt,共34页。
2024全国一轮数学(基础版)第2讲 充分条件、必要条件、充要条件课件PPT: 这是一份2024全国一轮数学(基础版)第2讲 充分条件、必要条件、充要条件课件PPT,共28页。PPT课件主要包含了链教材·夯基固本,激活思维,BCD,充分不必要,必要条件,基础回归,必要不充分,既不充分又不必要,研题型·融会贯通,举题说法等内容,欢迎下载使用。













