

2020-2021学年广西省贺州市高二(下)3月月考数学(文)试卷北师大版
展开1. 已知集合P=x|x2<4,Q=x|−1
2. 已知复数z满足z=61+i,则|z|=( )
A.2B.22C.3D.32
3. 函数f(x)=lnxx的导数是( )
A.1x2+1x2lnxB.−1x2+1x2lnxC.−1x2−1x2lnxD.1x2−1x2lnx
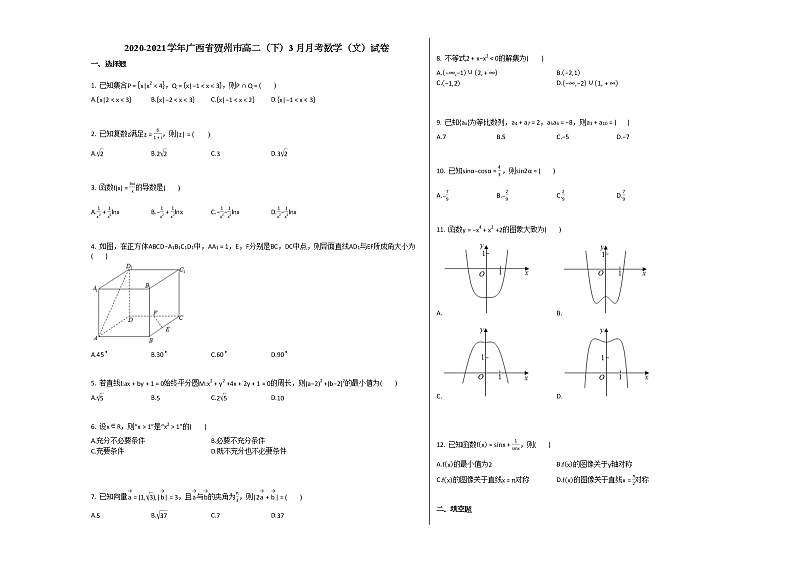
4. 如图,在正方体ABCD−A1B1C1D1中,AA1=1,E,F分别是BC,DC中点,则异面直线AD1与EF所成角大小为( )
A.45∘B.30∘C.60∘D.90∘
5. 若直线l:ax+by+1=0始终平分圆M:x2+y2+4x+2y+1=0的周长,则(a−2)2+(b−2)2的最小值为( )
A.5B.5C.25D.10
6. 设x∈R,则“x>1”是“x2>1”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
7. 已知向量a→=(1,3),|b→|=3,且a→与b→的夹角为π3,则|2a→+b→|=( )
A.5B.37C.7D.37
8. 不等式2+x−x2<0的解集为( )
A.−∞,−1∪2,+∞B.−2,1
C.−1,2D.−∞,−2∪1,+∞
9. 已知{an}为等比数列,a4+a7=2,a5a6=−8,则a1+a10=( )
A.7B.5C.−5D.−7
10. 已知sinα−csα=43 ,则sin2α=( )
A.−79B.−29C.29D.79
11. 函数y=−x4+x2+2的图象大致为( )
A.B.
C.D.
12. 已知函数fx=sinx+1sinx,则( )
A.fx的最小值为2B.fx的图像关于y轴对称
C.fx的图像关于直线x=π对称D.fx的图像关于直线x=π2对称
二、填空题
已知向量a→=1,2,b→=2,−2,c→=1,λ,若c→//2a→+b→,则λ=________.
已知实数x,y满足约束条件x+y−4≤0,x−2y+2≥0,y≥0,则z=x+2y的最大值为________.
已知曲线y=x2−3lnx的一条切线的斜率为−1,则该切线的方程为________.
已知双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若F1A→=AB→,F1B→⋅F2B→=0,则C的离心率为________.
三、解答题
△ABC中,角A,B,C的对边长分别为a,b,c,满足sin2B+sin2C−sin2A=3sinBsinC.
(1)求角A的大小;
(2)若a=1,B=π3,求△ABC的面积.
如图,四边形ABCD为正方形, PD⊥平面ABCD, PD=DC=2,点E,F分别为AD,PC的中点.
(1)证明: DF//平面PBE;
(2)求四面体C−PBE的体积.
为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参与文体活动是否有关,学校对200名学生做了问卷调查,2×2列联表如下:
已知在200人中随机抽取1人,抽到学习积极性不高的学生的概率为25.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:K2=nad−bc2a+bc+da+cb+d,其中n=a+b+c+d.
已知椭圆的中心在原点,焦点在x轴上,离心率为32,且过点P−3,12.
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A,B两点,求弦AB的长.
已知关于x的函数f(x)=−13x3+bx2+cx+bc,其导函数为f′(x),且函数f(x)在x=1处有极值−43.
(1)求实数b,c的值;
(2)求函数f(x)在[−1, 2]上的最大值和最小值.
已知等差数列an和等比数列bn中, a1=b1=1,公差d=2,公比q=3,cn=an⋅bn.
(1)求数列cn的通项公式;
(2)求数列cn的前n项和Sn.
参考答案与试题解析
2020-2021学年广西省贺州市高二(下)3月月考数学(文)试卷
一、选择题
1.
【答案】
C
【考点】
交集及其运算
【解析】
先化简集合P,再利用集合的交集运算求解即可.
【解答】
解:集合P=x|x2<4={x|−2
2.
【答案】
D
【考点】
复数的模
复数代数形式的乘除运算
【解析】
此题暂无解析
【解答】
解:因为z=61+i=61−i1+i1−i=3−3i,
所以|z|=32.
故选D.
3.
【答案】
D
【考点】
导数的运算
【解析】
此题暂无解析
【解答】
解:∵ f(x)=lnxx,
∴ f′(x)=1x×x−1×lnxx2=1−lnxx2=1x2−1x2lnx.
故选D.
4.
【答案】
C
【考点】
异面直线及其所成的角
【解析】
通过作平行线将异面直线所成角转化为相交直线所成角或其补角.
【解答】
解:取CC1的中点G,连EG,BC1,
易得EG // BC1 // AD1,
所以异面直线AD1与EF所成角是∠FEG或其补角,
在三角形EFG中,EF=EG=FG,
∴ ∠FEG=60∘.
故选C.
5.
【答案】
B
【考点】
直线和圆的方程的应用
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解:由题知圆M的圆心坐标为(−2,−1),
直线l平分圆M的周长,
则直线l一定过圆心,
∴ −2a−b+1=0,
∴ 2a+b=1.
∵ (a−2)2+(b−2)2是(a,b),(2,2)两点距离的平方,
∴ (2,2)到直线2a+b−1=0的距离为(a−2)2+(b−2)2的最小值,
∴ 距离d=522+12=5,
∴ 最小值为d2=5.
故选B.
6.
【答案】
A
【考点】
必要条件、充分条件与充要条件的判断
【解析】
由不等式x2>1的解集,进行充分、必要性进行判断即可.
【解答】
解:x2>1即x>1或x<−1,
所以由x>1可以得出x2>1,充分性成立,
由x2>1,不一定得出x>1,必要性不成立,
所以x>1是x2>1的充分不必要条件.
故选A.
7.
【答案】
B
【考点】
向量模长的计算
数量积表示两个向量的夹角
向量的模
【解析】
此题暂无解析
【解答】
解:∵ a→=(1,3),
∴ |a→|=2,
又∵ |b→|=3,a→与b→的夹角为π3,
∴ |2a→+b→|2=4|a→|2+4a→⋅b→+|b→|2
=4×4+4×2×3×csπ3+9
=37.
则|2a→+b→|=37.
故选B.
8.
【答案】
A
【考点】
一元二次不等式的解法
【解析】
通过因式分解,利用一元二次不等式的解法即可得出.
【解答】
解:不等式2+x−x2<0化为(x−2)(x+1)>0,
解得x>2或x<−1.
∴ 不等式2+x−x2<0的解集是(−∞, −1)∪(2, +∞).
故选A.
9.
【答案】
D
【考点】
等比数列的性质
【解析】
由a4+a7=2,及a5a6=a4a7=−8可求a4,a7,进而可求公比q,代入等比数列的通项可求a1,a10,即可.
【解答】
解:∵ a4+a7=2,由等比数列的性质可得,a5a6=a4a7=−8,
∴ a4=4,a7=−2或a4=−2,a7=4,
当a4=4,a7=−2时,q3=−12,
∴ a1=−8,a10=1,
∴ a1+a10=−7,
当a4=−2,a7=4时,q3=−2,则a10=−8,a1=1,
∴ a1+a10=−7,
综上可得,a1+a10=−7.
故选D.
10.
【答案】
A
【考点】
二倍角的正弦公式
【解析】
此题暂无解析
【解答】
解:(sinα−csα)2=169,
又sin2α+cs2α=1,
所以1−2sinαcsα=169,
所以2sinαcsα=−79,
因此sin2α=−79.
故选A.
11.
【答案】
D
【考点】
利用导数研究函数的单调性
函数的图象变换
【解析】
根据函数图象的特点,求函数的导数利用函数的单调性进行判断即可.
【解答】
解:函数过定点(0, 2),排除A,B.
函数的导数f′(x)=−4x3+2x=−2x(2x2−1),
由f′(x)>0得2x(2x2−1)<0,
得x<−22或0
得x>22或−22
12.
【答案】
D
【考点】
函数的对称性
诱导公式
函数最值的应用
【解析】
设sinx=t,则y=f(x)=t+1t,t∈[−1, 1],由对勾函数的图象和性质可得,y≥2或y≤−2,故可判断A,根据奇偶性定义可以判断B正误;根据对称性的定义可以判断C,D的正误.
【解答】
解:A,由sinx≠0可得函数的定义域为{x|x≠kπ, k∈Z},故定义域关于原点对称;
设sinx=t,则y=f(x)=t+1t,t∈[−1, 1],
由对勾函数的图象和性质得,y≥2或y≤−2,故A错误;
B,因为f(−x)=sin(−x)+1sin(−x)=−(sinx+1sinx)=−f(x),
故f(x)是奇函数,且定义域关于原点对称,故图象关于原点中心对称,故B错误;
C,f(π+x)=sin(π+x)+1sin(π+x)=−sinx−1sinx,
f(π−x)=sin(π−x)+1sin(π−x)=sinx+1sinx,
故f(π+x)≠f(π−x),f(x)的图象不关于直线x=π对称,故C错误;
D,又f(π2+x)=sin(π2+x)+1sin(π2+x)=csx+1csx,
f(π2−x)=sin(π2−x)+1sin(π2−x)=csx+1csx,
故f(π2+x)=f(π2−x),定义域为{x|x≠kπ, k∈Z},
f(x)的图象关于直线x=π2对称,故D正确.
故选D.
二、填空题
【答案】
12
【考点】
平面向量共线(平行)的坐标表示
平面向量的坐标运算
【解析】
首先根据向量的运算法则,求得向量2a→+b→的坐标,之后应用向量平行时坐标所满足的条件,得到相应的等量关系式,求得结果.
【解答】
解:∵ a→=(1,2),b→=(2,−2),
∴ 2a→+b→=(2,4)+2,−2=4,2.
∵ c→//2a→+b→,
∴ 2−4λ=0,
∴ λ=12.
故答案为:12.
【答案】
6
【考点】
简单线性规划
【解析】
此题暂无解析
【解答】
解:依题意组,不等式组表示的可行域如图所示,
由z=x+2y得y=−12x+12z,
目标函数在过点A(2,2)时取得最大值6.
故答案为:6.
【答案】
x+y−2=0
【考点】
利用导数研究曲线上某点切线方程
【解析】
求出原函数的导函数,设出切点坐标,利用曲线在切点处的导数值为−1求得切点坐标,再由直线方程的点斜式得答案.
【解答】
解:由y=x2−3lnx,得y′=2x−3x,
设切点为(x0, y0),则y′|x=x0=2x0−3x0=−1,
即2x02+x0−3=0,
解得x0=−32(舍)或x0=1.
∴ 切点为(1, 1),
则切线方程为y−1=−1×(x−1),即x+y−2=0.
故答案为:x+y−2=0.
【答案】
2
【考点】
数量积判断两个平面向量的垂直关系
双曲线的离心率
双曲线的渐近线
【解析】
由题意画出图形,结合已知可得F1B⊥OA,写出F1B的方程,与y=bax联立求得B点坐标,再由斜边的中线等于斜边的一半求解.
【解答】
解:如图,F1A→=AB→,F1B→⋅F2B→=0,
∴ OA⊥F1B,
则F1B:y=abx+c ,
联立y=abx+c,y=bax,
解得Ba2cb2−a2,abcb2−a2,
则OB2=a4c2(b2−a2)2+a2b2c2(b2−a2)2=c2,
整理得:b2=3a2 ,
又c2−a2=3a2,
即4a2=c2,
故c2a2=4,
则e=ca=2.
故答案为:2.
三、解答题
【答案】
解:(1)因为sin2B+sin2C−sin2A=3sinBsinC,
由正弦定理可得: b2+c2−a2=3bc,
所以csA=b2+c2−a22bc=32,
所以A=π6.
(2)因为A=π6,B=π3,所以C=π2,
所以b=3,可得S△ABC=32.
【考点】
余弦定理
正弦定理
【解析】
此题暂无解析
【解答】
解:(1)因为sin2B+sin2C−sin2A=3sinBsinC,
由正弦定理可得: b2+c2−a2=3bc,
所以csA=b2+c2−a22bc=32,
所以A=π6.
(2)因为A=π6,B=π3,所以C=π2,
所以b=3,可得S△ABC=32.
【答案】
(1)证明:取PB的中点G,连接EG、FG,
则FG // BC,且FG=12BC.
∵ DE // BC且DE=12BC,
∴ DE // FG且DE=FG,
∴ 四边形DEGF为平行四边形,
∴ DF // EG,又EG⊂平面PBE,DF⊄平面PBE,
∴ DF // 平面PBE;
(2)解:∵ PD=DC=2,ABCD为正方形,PD⊥面ABCD,
∴ VC−PBE=VP−CBE=13⋅S△CBE⋅ℎ
=13×12×2×2×2=43.
【考点】
直线与平面平行的判定
柱体、锥体、台体的体积计算
点、线、面间的距离计算
【解析】
此题暂无解析
【解答】
(1)证明:取PB的中点G,连接EG、FG,
则FG // BC,且FG=12BC.
∵ DE // BC且DE=12BC,
∴ DE // FG且DE=FG,
∴ 四边形DEGF为平行四边形,
∴ DF // EG,又EG⊂平面PBE,DF⊄平面PBE,
∴ DF // 平面PBE;
(2)解:∵ PD=DC=2,ABCD为正方形,PD⊥面ABCD,
∴ VC−PBE=VP−CBE=13⋅S△CBE⋅ℎ
=13×12×2×2×2=43.
【答案】
解:(1)根据题意,全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为25,
则学习积极性不高的有200×25=80人,
据此可得:列联表如下:
(2)根据题意,由列联表可得:
K2=200×80×60−20×402120×80×100×100≈33.33>10.828,
故有99.9%的把握认为学习积极性高与参加文体活动有关.
(3)根据题意,从不参加文体活动的同学中按照分层抽样的方法选取5人,有2人学习积极性高,设为A,B,有3人学习积极性不高,设为C,D,E,
从中选取2人,,
有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10种情况,
其中至少有1人学习积极性不高的有AC,AD,AE,BC,BD,BE,CD,CE,DE,共9种情况,
则至少有1人学习积极性不高的概率P=910.
【考点】
独立性检验
分层抽样方法
列举法计算基本事件数及事件发生的概率
【解析】
(1)计算学习积极性不高的有200×25=80人,完善列联表得到答案
(2)K2≈33.33>10.828,对比临界值表得到答案
(3)有2人学习积极性高,设为A、B,有3人学习积极性不高,设为C、D、E,列出所有情况,统计满足条件的情况,得到概率.
【解答】
解:(1)根据题意,全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为25,
则学习积极性不高的有200×25=80人,
据此可得:列联表如下:
(2)根据题意,由列联表可得:
K2=200×80×60−20×402120×80×100×100≈33.33>10.828,
故有99.9%的把握认为学习积极性高与参加文体活动有关.
(3)根据题意,从不参加文体活动的同学中按照分层抽样的方法选取5人,有2人学习积极性高,设为A,B,有3人学习积极性不高,设为C,D,E,
从中选取2人,,
有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10种情况,
其中至少有1人学习积极性不高的有AC,AD,AE,BC,BD,BE,CD,CE,DE,共9种情况,
则至少有1人学习积极性不高的概率P=910.
【答案】
解:(1)设椭圆方程为x2a2+y2b2=1(a>b>0),椭圆的半焦距为c,
由椭圆C的离心率为32,可得ca=32,
∴a2−b2a2=34.①
∵椭圆过点−3,12,
∴3a2+14b2=1,②
由①②解得:b2=1,a2=4,
故椭圆C的方程为x24+y2=1.
(2)设A,B的坐标分别为Ax1,y1,Bx2,y2,
由椭圆的方程知a2=4,b2=1,c2=3,F3,0.
则直线l的方程为y=x−3.
联立y=x−3,x24+y2=1,
得5x2−83x+8=0.
故Δ=192−160=32>0,x1+x2=835,x1x2=85,
|AB|=2|x1−x2|=2⋅x1+x22−4x1x2
=28352−325=85.
【考点】
椭圆的标准方程
椭圆的离心率
与椭圆有关的中点弦及弦长问题
【解析】
(1)先设椭圆的方程,再利用的椭圆C的离心率为32,且过点−3,12,即可求得椭圆C的方程;
(2)设出A、B的坐标,由椭圆方程求出椭圆右焦点坐标,得到A、B所在直线方程,与椭圆方程联立,化为关于x的一元二次方程,利用根与系数的关系可得A、B横坐标的和与积,代入弦长公式求弦AB的长.
【解答】
解:(1)设椭圆方程为x2a2+y2b2=1(a>b>0),椭圆的半焦距为c,
由椭圆C的离心率为32,可得ca=32,
∴a2−b2a2=34.①
∵椭圆过点−3,12,
∴3a2+14b2=1,②
由①②解得:b2=1,a2=4,
故椭圆C的方程为x24+y2=1.
(2)设A,B的坐标分别为Ax1,y1,Bx2,y2,
由椭圆的方程知a2=4,b2=1,c2=3,F3,0.
则直线l的方程为y=x−3.
联立y=x−3,x24+y2=1,
得5x2−83x+8=0.
故Δ=192−160=32>0,x1+x2=835,x1x2=85,
|AB|=2|x1−x2|=2⋅x1+x22−4x1x2
=28352−325=85.
【答案】
解:(1)因为fx=−13x3+bx2+cx+bc,
所以f′x=−x2+2bx+c.
因为函数fx在x=1处有极值−43,
所以f′1=−1+2b+c=0,f1=−13+b+c+bc=−43,
解得b=1,c=−1或b=−1,c=3.
(i)当b=1,c=−1时,f′x=−x−12≤0,
所以f(x)在R上单调递减,不存在极值;
(ii)当b=−1,c=3时,f′x=−x+3x−1,
当x∈(−3, 1)时,f(x)单调递增;
当x∈(1, +∞)时,f(x)单调递减.
所以f(x)在x=1处存在极大值,符合题意.
综上所述,满足条件的值为b=−1,c=3.
(2)由(1)知fx=−13x3−x2+3x−3,
则f′x=−x2−2x+3.
令f′x=−x+3x−1=0,得x1=−3,x2=1,
所以fx,f′x的变化如下表:
所以fxmin=f−1=−203,fxmax=f1=−43.
【考点】
利用导数研究函数的极值
利用导数研究函数的最值
【解析】
(1)求出函数的导数,结合函数的极值得到关于a,b的方程组,解出验证即可;
(2)求出函数的导数,根据函数的单调性求出函数的最值即可.
【解答】
解:(1)因为fx=−13x3+bx2+cx+bc,
所以f′x=−x2+2bx+c.
因为函数fx在x=1处有极值−43,
所以f′1=−1+2b+c=0,f1=−13+b+c+bc=−43,
解得b=1,c=−1或b=−1,c=3.
(i)当b=1,c=−1时,f′x=−x−12≤0,
所以f(x)在R上单调递减,不存在极值;
(ii)当b=−1,c=3时,f′x=−x+3x−1,
当x∈(−3, 1)时,f(x)单调递增;
当x∈(1, +∞)时,f(x)单调递减.
所以f(x)在x=1处存在极大值,符合题意.
综上所述,满足条件的值为b=−1,c=3.
(2)由(1)知fx=−13x3−x2+3x−3,
则f′x=−x2−2x+3.
令f′x=−x+3x−1=0,得x1=−3,x2=1,
所以fx,f′x的变化如下表:
所以fxmin=f−1=−203,fxmax=f1=−43.
【答案】
解:(1)由等差数列通项公式知:
an=a1+n−1d=1+2n−1=2n−1,
由等比数列通项公式知:bn=b1qn−1=3n−1,
∴ cn=2n−1⋅3n−1.
(2)由(1)知:Sn=1×30+3×31+5×32+⋯+
(2n−3)×3n−2+(2n−1)×3n−1,
∴ 3Sn=1×31+3×32+5×33+⋯+
2n−3×3n−1+2n−1×3n,
两式作差得:−2Sn=1−2n−1×3n+2×3+32+⋯+3n−1,
∴ −2Sn=1−2n−1×3n+2×3−3n1−3
=1−2n−1×3n+3n−3
=−2+2−2n⋅3n,
∴ Sn=n−1⋅3n+1.
【考点】
等差数列的通项公式
等比数列的通项公式
数列的求和
【解析】
此题暂无解析
【解答】
解:(1)由等差数列通项公式知:
an=a1+n−1d=1+2n−1=2n−1,
由等比数列通项公式知:bn=b1qn−1=3n−1,
∴ cn=2n−1⋅3n−1.
(2)由(1)知:Sn=1×30+3×31+5×32+⋯+
(2n−3)×3n−2+(2n−1)×3n−1,
∴ 3Sn=1×31+3×32+5×33+⋯+
2n−3×3n−1+2n−1×3n,
两式作差得:−2Sn=1−2n−1×3n+2×3+32+⋯+3n−1,
∴ −2Sn=1−2n−1×3n+2×3−3n1−3
=1−2n−1×3n+3n−3
=−2+2−2n⋅3n,
∴ Sn=n−1⋅3n+1.参加文体活动
不参加文体活动
合计
学习积极性高
80
学习积极性不高
60
合计
200
P(K2≥k0)
0.15
0.10
0.05
0.025
0.005
0.001
k0
2.072
2.706
3.841
5.024
7.879
10.828
参加文体活动
不参加文体活动
合计
学习积极性高
80
40
120
学习积极性不高
20
60
80
合计
100
100
200
参加文体活动
不参加文体活动
合计
学习积极性高
80
40
120
学习积极性不高
20
60
80
合计
100
100
200
x
−1
(−1, 1)
1
(1, 2)
2
f′(x)
+
0
−
f(x)
−203
单调递增
−43
单调递减
−113
x
−1
(−1, 1)
1
(1, 2)
2
f′(x)
+
0
−
f(x)
−203
单调递增
−43
单调递减
−113
2020-2021年广西省贺州市高三(上)1月月考数学(文)试卷北师大版: 这是一份2020-2021年广西省贺州市高三(上)1月月考数学(文)试卷北师大版,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年广西省贺州市高三(上)12月月考数学(文)试卷北师大版: 这是一份2020-2021学年广西省贺州市高三(上)12月月考数学(文)试卷北师大版,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年广西省贺州市高二(下)期末考试数学(文)试卷北师大版: 这是一份2020-2021学年广西省贺州市高二(下)期末考试数学(文)试卷北师大版,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












