2021届北京市房山区高三数学一模试卷及答案

这是一份2021届北京市房山区高三数学一模试卷及答案，共11页。试卷主要包含了单项选择题，填空题，双空题，解答题等内容，欢迎下载使用。


北京市房山区高三数学一模试卷
一、单项选择题
1.假设集合 ，集合 ，那么 等于〔    〕
A.                        B.                        C.                        D. {1}



2.以下函数中，值域为 且为偶函数的是〔    〕
A.                              B.                              C.                              D. 



3. ， ，且 ，那么以下各式中一定成立的是〔    〕
A.                                B.                                C.                                D. 



4.将函数 的图象向左平移 个单位得到函数 的图象，那么函数 的图象的一条对称轴方程为〔    〕
A.                              B.                              C.                              D. 



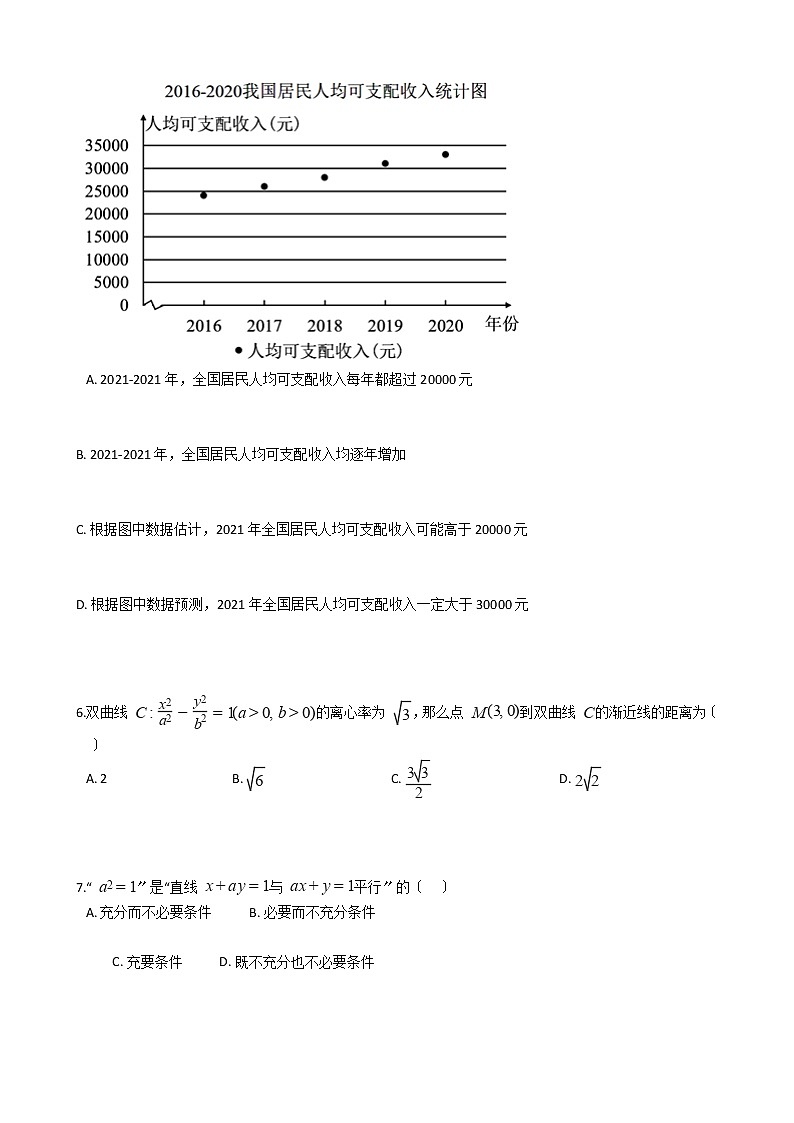
5.“十三五〞期间，我国大力实施就业优先政策，促进居民人均收入持续增长.下面散点图反映了2021-2021年我国居民人均可支配收入(单位：元)情况.根据图中提供的信息，以下判断不正确的选项是〔    〕

A. 2021-2021年，全国居民人均可支配收入每年都超过20000元


B. 2021-2021年，全国居民人均可支配收入均逐年增加


C. 根据图中数据估计，2021年全国居民人均可支配收入可能高于20000元


D. 根据图中数据预测，2021年全国居民人均可支配收入一定大于30000元



6.双曲线 的离心率为 ，那么点 到双曲线 的渐近线的距离为〔    〕
A. 2                                       B.                                        C.                                        D. 



7.“ 〞是“直线 与 平行〞的〔    〕
A. 充分而不必要条件           B. 必要而不充分条件

           C. 充要条件           D. 既不充分也不必要条件



8.在矩形 中， 与 相交于点 ， 是线段 的中点，假设 ，那么 的值为〔    〕
A.                                          B. -1                                         C. 1                                         D. 



9.等差数列 的前 项和为 ，且 ， ，那么下面结论错误的选项是〔    〕
A.                      B. 

                     C.                      D. 与 均为 的最小值



10.祖暅是我国南北朝时代伟大的科学家，他在实践的根底上提出了体积计算的原理：“幂势既同，那么积不容异〞.意思是：如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等，此即祖暅原理.利用这个原理求球的体积时，需要构造一个满足条件的几何体，该几何体三视图如下列图，用一个与该几何体的下底面平行且相距为 的平面截该几何体，那么截面面积为〔    〕

A. 4π                                B.                                 C.                                 D. 



二、填空题
11. 为虚数单位，计算 ________．
12.的展开式的常数项是________〔用数字作答〕．
13.设 ， ，那么使得命题“假设 ，那么 〞为假命题的一组 的值是________.
14.设函数 的定义域为 ，假设对于任意 ，存在 ，使 ( 为常数)成立，那么称函数 在 上的“半差值〞为 .以下四个函数中，满足所在定义域上“半差值〞为 的函数是________(填上所有满足条件的函数序号).① ；② ；③ ；④ .
三、双空题
15.抛物线 的焦点为 ，那么点 的坐标为________，假设抛物线上一点 到 轴的距离为2，那么 ________.
四、解答题
16.如图，在直三棱柱 中， ， ， ， 为 上一点，且 .

〔1〕求证：平面 平面 ；
〔2〕求直线 与平面 所成角的正弦值.
17.在 中， ，再从条件①､条件②､条件③这三个条件中选择一个作为，求：
〔1〕的值；
〔2〕的面积.
条件①： 边上的高为 ；条件②： ；条件③： .
注：如果选择多个条件分别解答，按第一个解答计分.
18.单板滑雪型池比赛是冬奥会比赛中的一个工程，进入决赛阶段的名运发动按照预赛成绩由低到高的出场顺序轮流进行三次滑行，裁判员根据运发动的腾空高度､完成的动作难度和效果进行评分，最终取单次最高分作为比赛成绩.现有运发动甲､乙二人在2021赛季单板滑雪 型池世界杯分站比赛成绩如下表：
分站
运发动甲的三次滑行成绩
运发动乙的三次滑行成绩
第1次
第2次
第3次
第1次
第2次
第3次
第1站





0
第2站






第3站

0




第4站






第5站






假设甲､乙二人每次比赛成绩相互独立.
〔1〕从上表5站中随机选取1站，求在该站运发动甲的成绩高于运发动乙的成绩的概率；
〔2〕从上表5站中任意选取2站，用 表示这2站中甲的成绩高于乙的成绩的站数，求 的分布列和数学期望；
〔3〕假设从甲､乙2人中推荐1人参加2022年北京冬奥会单板滑雪 型池比赛，根据以上数据信息，你推荐谁参加，并说明理由.
(注：方差 ，其中 为 ， ，…， 的平均数)
19.函数 .
〔1〕求曲线 在点 处的切线方程；
〔2〕假设 ，求证： ；
〔3〕设 ，是否存在唯一的自然数 ，使得 与 的图象在区间 上有两个不同的公共点？假设存在，试求出 的值，假设不存在，请说明理由.
20.椭圆 过点 ，离心率为 .
〔1〕求椭圆 的方程；
〔2〕设点 为椭圆 的上顶点， 、 是椭圆 上两个不同的动点〔不在 轴上〕，直线 、 的斜率分别为 、 ，且 ，求证：直线 过定点 .
21.对于数列 ，记 ，其中 表示 这 个数中最大的数，并称数列 是 的“控制数列〞，如数列 的“控制数列〞是 .
〔1〕假设各项均为正整数的数列 的“控制数列〞为 ，写出所有的 ；
〔2〕设 .
〔i〕当 时，证明：存在正整数 ，使得 是等差数列；
〔ii〕当 时，求 的值(结果可含 ).

答案解析局部
一、单项选择题
1.【解析】【解答】因为集合 ，集合 ，
所以 ，
故答案为：A

【分析】根据题意由交集的定义即可得出答案。
2.【解析】【解答】A：因为函数 的值域为 ，所以本选项不符合题意；
B：设 ，因为 ，所以该函数不是偶函数，因此不符合题意；
C：设 ，显然 ，因为 ，所以该函数是偶函数，故符合题意；
D：设 ，因为 ，所以该函数是奇函数，故不符合题意,
故答案为：C

【分析】根据题意由余弦函数、一次函数、二次函数以及指数函数的性质即可求出函数的值域，再由偶函数的定义对选项逐一判断即可得出答案。
3.【解析】【解答】解：因为 ， ，且 ，
对于A：假设 ， ，显然 ，A不符合题意；
对于B：因为函数 在定义域 上单调递增，所以 ，B符合题意；
对于C：假设 ，那么 ，C不符合题意；
对于D：假设 ， ，那么 ，D不符合题意；
故答案为：B

【分析】根据题意由特殊值法代入结合不等式的性质对选项逐一判断即可得出答案。
4.【解析】【解答】解：将函数 的图象向左平移 个单位，得到
令 ，解得
当 时，
故答案为：C

【分析】根据题意由函数平移的性质整理即可得到函数的解析式，再由正弦函数的性质即可得出， 对k赋值计算出x的值即可。
5.【解析】【解答】A：由散点图可知：2021-2021年，全国居民人均可支配收入每年都超过20000元，所以本判断正确；
B：由散点图可知：2021-2021年，全国居民人均可支配收入均逐年增加，所以本判断正确；
C：根据图中数据估计，2021年全国居民人均可支配收入可能高于20000元，所以本判断正确；
D：根据图中数据预测，2021年全国居民人均可支配收入有可能大于30000元，不是一定大于30000元，所以本判断不正确，
故答案为：D

【分析】根据题意结合散点图的性质以及图表中的数据对选项逐一判断即可得出答案。
6.【解析】【解答】解：根据题意，双曲线 的离心率为 ，
其焦点在 轴上，其渐近线方程为 ，
又由其离心率 ，那么 ，
那么 ，即 ，
那么其渐近线方程 ；
那么点 到双曲线 的渐近线的距离
故答案为：B．

【分析】首先由双曲线的简单性质即可求出离心率的值再由离心率的公式，即可得出再由双曲线里a、b、c的关系即可求出， 从而得出渐近线的方程再结合点到直线的距离公式计算出结果即可。
7.【解析】【解答】因为直线 与 平行，
所以 且两直线的斜率相等即 解得 ；
而当 时直线 为 ，同时 为 ，两直线重合不满足题意；当 时， 与 平行，满足题意；
故 ，
根据小范围推大范围可得： 是 的必要不充分条件.
故答案为：B

【分析】 根据直线平行的等价条件求出a的值，利用充分条件和必要条件的定义进行判断即可．
8.【解析】【解答】因为 ，
所以 ，
故答案为：A

【分析】根据题意由向量的线性运算结合向量的加、减运算法那么，再由条件即可求出m与n的值。
9.【解析】【解答】对于A选项，由 可得 ，A选项正确；
对于C选项，由 可得 ， ，C选项错误；
对于D选项，由 可得 ，且 ， ， ，
所以，当 且 时， ，且 ，那么 与 均为 的最小值，D选项正确；
对于B选项， ， ，当 时， ，
所以， ，B选项正确.
故答案为：C.

【分析】 由可得a8＜0，a9=0，a10＞0，d＞0，然后结合各选项进行分析即可求解．
10.【解析】【解答】由题意可知，该几何体为底面半径为2，高为2的圆柱，从上面挖去一个半径为2，高为2的圆锥，所剩下的局部，如下列图：

所以截面为环形，外圆的半径为2，内圆的半径为h，所以面积为：
故答案为：D

【分析】 根据三视图知该几何体为一个圆柱挖去一个圆锥，得到截面为圆环，根据圆环面积公式计算即可．
二、填空题
11.【解析】【解答】解：复数 ．
【分析】首先由复数代数形式的运算性质整理化简即可得出答案。
12.【解析】【解答】因为 展开式的第 项为 ，
令 ，那么 ，
所以展开式的常数项为 .
故答案为：-160.

【分析】首先求出二项展开式的通项公式再由条件令 ， 求解出k的值，再把数值代入奥通项公式计算出结果即可。
13.【解析】【解答】解：要使命题“假设 ，那么 〞为假命题；
那么存在 ， ， ，且
所以 且 ，取 即可满足条件，此题属于开放性题，只需填写符合 且 的值即可；
故答案为：满足a+b＞1且ab≤1即可

【分析】由对数的运算性质结合假命题的定义即可得出答案。
14.【解析】【解答】①： ，当 时， ，该函数此时单调递增，
当 时， ，该函数此时单调递减，所以当 时，函数有最小值 ，
假设 是“半差值〞为 的函数，因此有 ，存在 ，使 成立，即 ，对于 ， ，而 ，显然 ，不一定存在 ，使 成立，故本函数不符合题意；
②：因为函数 的值域是全体实数集，所以对于任意 ，存在 ，使 成立，符合题意；
③：因为函数 的的值域是全体实数集，所以对于任意 ，存在 ，使 成立，符合题意；
④：假设 是实数集上的“半差值〞为 的函数，因此有 ，存在 ，使 成立，即 ，对于 ， ，而 ，显然 恒不成立，故假设不成立，所以本函数不符合题意，
故答案为：②③

【分析】 由题意可得，对定义域中任意的x，存在y，使得f〔y〕=f〔x〕-4，结合选项分别判断函数的值域即可求解．
三、双空题
15.【解析】【解答】由抛物线 的方程可知： ，所以点 的坐标为 ；
因为该抛物线的准线方程为 ，所以 ，
故答案为：〔2,0〕；4

【分析】首先由抛物线的简单性质即可求出点P以及焦点的坐标，准线方程再由点到直线的距离公式计算出结果即可。
四、解答题
16.【解析】【分析】(1)解法一：首先由直三棱柱的几何性质即可得出线面垂直，由线面垂直的性质定理即可得出线线垂直，借助勾股定理代入数值计算出线线垂直，再由线面垂直以及面面垂直的判定定理即可得证出结论。解法二：首先由直三棱柱的几何性质即可得出线面垂直，由线面垂直的性质定理即可得出线线垂直，由此根据题意建立空间直角坐标系求出各个点的坐标以及向量和平面法向量的坐标，再由数量积的坐标公式即可求出平面的法向量的坐标，同理即可求出平面的法向量；结合空间数量积的运算公式代入数值即可得出， 由此即可得证出结论。
(2)由(1)的解法二，求出各个点以及向量和 平面 的法向量的坐标，结合空间数量积的运算公式代入数值即可求出夹角的余弦值，再由同角三角函数的根本关系式即可求出夹角的正弦值，由此得到 直线 与平面 所成角的正弦值 。
 
 
17.【解析】【分析】选①(1)在直角三角形中，由正弦公式计算出sinA的值，再由两角和的正弦公式代入数值计算出结果即可。
(2)根据题意在直角三角形中，由正弦公式代入数值计算出sinB的值，由此得出BC的值，再由三角形的面积公式计算出结果即可。
选② (1)根据题意由两角和的正弦公式代入数值计算出结果即可。
(2)由正弦定理计算出a的值，再由三角形的面积公式代入数值计算出结果即可。
选③ ，由a的值结合三角形的面积公式计算出结果即可。
18.【解析】【分析】(1)根据题意首先求出甲站和乙站的成绩，再由该站运发动甲的成绩高于运发动乙的成绩，结合古典概率计算出结果即可。
(2)根据题意求出X的取值，再由概率公式计算出对应每个X的概率值，由此即可得出 的分布列 并把数值代入到期望值公式计算出结果即可。
(3)根据题意由甲站和乙站的平均成绩以及方差公式计算出结果，与标准差进行比较即可得出结论。
 
19.【解析】【分析】(1)首先对函数求导再把点的坐标代入到导函数的解析式计算出切线的斜率，再由点斜式求出直线的方程。
(2)根据题意构造函数g(x)再对其求导结合导函数的性质即可得出函数g(x)的单调性，再由函数的单调性即可求出函数的极值。
(3)根据题意把函数图象的交点问题转化为函数零点的问题，再构造函数并对其求导利用导函数的性质即可得出函数的极值，由此得到以及结合零点存在性定理即可得出 在 内有两个零点，在 ， 内无零点， 内有唯一零点.，由此即可得证出结论。
 
 
20.【解析】【分析】(1)首先根据题意由椭圆的简单性质即可得出关于a、b、c的方程组求解出结果，由此即可得到椭圆的方程。
(2)根据题意首先求出点M的坐标，再设出点A与B的坐标以及直线的方程再联立直线与椭圆的方程，消去y等到关于x的一元二次方程，求解出方程的根关于k1的代数式，再由斜率的公式即可得到直线AN的斜率，同理即可求出直线BM的斜率，进而得到， 由此得出直线AB过的定点的坐标。
 
 
21.【解析】【分析】 (1)根据“控制数列〞的定义，写出数列{an}的各项即可。
(2)〔i〕利用二次函数的性质可知，当时函数f〔x〕单调递增，所以当
n≥m时，有an=bn ， 从而得出是等差数列． 〔ii〕对a的范围分情况讨论，利用作差法比较大小，得到b1 ， b2 ， b3 ， b4的值，从而求出的值即可。