2020-2021学年黑龙江省高二（上）期中数学试卷（文科）人教A版

这是一份2020-2021学年黑龙江省高二（上）期中数学试卷（文科）人教A版，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 用符号表示“点A在直线l上，l不在平面α内”，正确的是（ ）
A.A∈l，l∉αB.A⊂l，l⊄αC.A⊂l，l∈αD.A∈l，l⊄α

2. 已知空间中点A(x, 1, 2)和点B(2, 3, 4)，且|AB|=26，则实数x的值是（ ）
A.6或−2B.−6或2C.3或−4D.−3或4

3. 下列命题正确的是( )
A.若a>b，则ac2>bc2B.若a>b，c>d，则ac>bd
C.若ac2>bc2，则a>bD.若a>b，c>d，则a−c>b−d

4. 由不等式组x≥0y≥0x+y−1≤0 表示的平面区域（图中阴影部分）为（ ）
A.B.
C.D.

5. 一个几何体的三视图如图所示，则该几何体的侧面积为（ ）

A.3πB.4πC.2π+4D.4π+4

6. 下列说法正确的是（ ）
A.侧棱垂直于底面的棱柱一定是直棱柱
B.棱柱中两个互相平行的平面一定是棱柱的底面
C.棱柱中各条棱长都相等
D.棱柱的侧面是平行四边形，但它的底面一定不是平行四边形

7. 已知直线l1；2x+y−2＝0，l2:ax+4y+1＝0，若l1⊥l2，则a的值为（ ）
A.8B.2C.−12D.−2

8. 已知a // α，b⊂α，则直线a与直线b的位置关系是（ ）
A.平行B.相交或异面C.异面D.平行或异面

9. 已知直线l1：(3+a)x+4y−5+3a＝0与l2:2x+(5+a)y+8＝0平行，则a等于（ ）
A.−7或−1B.7或1C.−7D.−1

10. 下列命题正确的是（ ）
A.三点确定一个平面
B.一条直线和一个点确定一个平面
C.梯形可确定一个平面
D.圆心和圆上两点确定一个平面

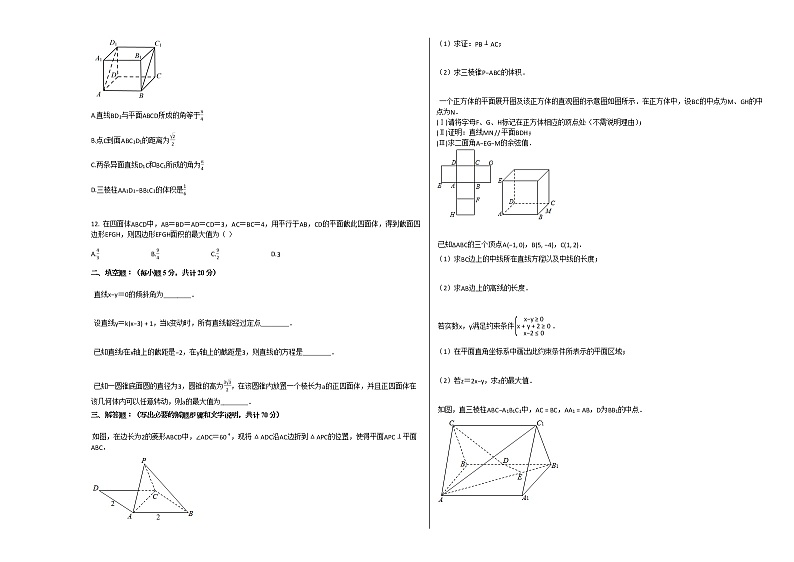
11. 如图，正方体ABCD−A1B1C1D1的棱长为1，则下列四个命题中正确的是（ ）

A.直线BD1与平面ABCD所成的角等于π4
B.点C到面ABC1D1的距离为22
C.两条异面直线D1C和BC1所成的角为π4
D.三棱柱AA1D1−BB1C1的体积是16

12. 在四面体ABCD中，AB＝BD＝AD＝CD＝3，AC＝BC＝4，用平行于AB，CD的平面截此四面体，得到截面四边形EFGH，则四边形EFGH面积的最大值为（ ）
A.43B.94C.92D.3
二、填空题：（每小题5分，共计20分）

直线x−y＝0的倾斜角为________．

设直线y＝k(x−3)+1，当k变动时，所有直线都经过定点________．

已知直线l在x轴上的截距是−2，在y轴上的截距是3，则直线l的方程是________．

已知一圆锥底面圆的直径为3，圆锥的高为332，在该圆锥内放置一个棱长为a的正四面体，并且正四面体在该几何体内可以任意转动，则a的最大值为________．
三、解答题：（写出必要的解题步骤和文字说明，共计70分）

如图，在边长为2的菱形ABCD中，∠ADC＝60∘，现将△ADC沿AC边折到△APC的位置，使得平面APC⊥平面ABC．

（1）求证：PB⊥AC；

（2）求三棱锥P−ABC的体积．

一个正方体的平面展开图及该正方体的直观图的示意图如图所示．在正方体中，设BC的中点为M、GH的中点为N．
(Ⅰ)请将字母F、G、H标记在正方体相应的顶点处（不需说明理由）；
(Ⅱ)证明：直线MN // 平面BDH；
(Ⅲ)求二面角A−EG−M的余弦值．


已知ΔABC的三个顶点A(−1, 0)，B(5, −4)，C(1, 2)．
（1）求BC边上的中线所在直线方程以及中线的长度；

（2）求AB边上的高线的长度．

若实数x，y满足约束条件x−y≥0x+y+2≥0x−2≤0 ．
（1）在平面直角坐标系中画出此约束条件所表示的平面区域；

（2）若z＝2x−y，求z的最大值．

如图，直三棱柱ABC−A1B1C1中，AC=BC，AA1=AB，D为BB1的中点．

(1)若E为AB1上的一点，且DE与直线CD垂直，求EB1AB1的值；

(2)在(1)的条件下，设异面直线AB1与CD所成的角为45∘，求直线DE与平面AB1C1所成角的正弦值．

如图，在棱长为2的正方体ABCD−A1B1C1D1中，E，F，M，N分别是棱AB，AD，A1B1，A1D1的中点，点P，Q分别在棱DD1，BB1上移动，且DP＝BQ＝λ(0<λ<2)．
(Ⅰ)当λ＝1时，证明：直线BC1 // 平面EFPQ；
(Ⅱ)是否存在λ，使面EFPQ与面PQMN所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．

参考答案与试题解析
2020-2021学年黑龙江省高二（上）期中数学试卷（文科）
一、选择题：（每个小题仅有一个选项符合题目要求，每小题5分，共计60分）
1.
【答案】
D
【考点】
平面的基本性质及推论
【解析】
直接利用空间点与直线，直线与面的位置关系写出结果即可．
【解答】
“点A在直线l上，l不在平面α内”，符号表示为：A∈l，l⊄α，
2.
【答案】
A
【考点】
空间两点间的距离公式
【解析】
根据空间中两点间的距离公式，列出方程求出实数x的值．
【解答】
点A(x, 1, 2)和点B(2, 3, 4)，且|AB|=26，
∴ (x−2)2+(1−3)2+(2−4)2=26，
化简得(x−2)2＝16，
解得x＝6或x＝−2，
∴ 实数x的值是6或−2．
3.
【答案】
C
【考点】
不等式的基本性质
【解析】
由不等式的基本性质逐一判断即可．
【解答】
解：对于A，当c=0时，ac2=bc2，故A错误；
对于B，取a=2，b=−1，c=−2，d=−3，则ac对于C，若ac2>bc2，可知c2>0，则a>b，故C正确；
对于D，取a=−1，b=−2，c=3，d=1，则a−c故选C.
4.
【答案】
C
【考点】
二元一次不等式（组）与平面区域
【解析】
根据不等式组和平面区域的关系即可得到结论．
【解答】
由不等式组可知，平面区域位于直线x＝0的右侧，y＝0的上方，
直线x+y−1＝0的下方，
故对应的平面区域为C，
5.
【答案】
C
【考点】
由三视图求体积
【解析】
首先把三视图转换为几何体的直观图，进一步求出几何体的侧面积．
【解答】
解：根据几何体的三视图转换为直观图为：该几何体为半圆柱，
如图所示：
由于底面为半径为1的半圆形，所以S=π⋅1⋅2=2π，
所以：S侧=2π+2×2=2π+4．
故选C．
6.
【答案】
A
【考点】
棱柱的结构特征
【解析】
根据直棱柱的定义和性质，可判断选项A；列举棱柱中两个互相平行的平面，可判断选项B；由侧棱与棱的区别，可判断选项C；举特例，例如长方体，可判断选项D．
【解答】
选项A，由直棱柱的定义和性质可知选项A正确；
选项B，棱柱中两个互相平行的平面也可能是棱柱的侧面，即B错误；
选项C，棱柱中的各条侧棱都相等，并不是每条棱都相等，即C错误；
选项D，长方体是棱柱，它的侧面和底面都是平行四边形，即D错误．
7.
【答案】
D
【考点】
直线的一般式方程与直线的垂直关系
【解析】
由直线方程分别求出l1、l2的斜率，再由l1⊥l2得斜率之积为−1，列出方程并求出a的值．
【解答】
由题意得，l1:2x+y−2＝0，l2:ax+4y+1＝0，
则直线l1的斜率是−2，l2的斜率是−a4，
∵ l1⊥l2，∴ (−a4)×(−2)＝−1，解得a＝−2，
8.
【答案】
D
【考点】
空间中直线与直线之间的位置关系
【解析】
由直线a // 平面α，直线b在平面α内，知a // b，或a与b异面．
【解答】
∵ 直线a // 平面α，直线b在平面α内，
∴ a // b，或a与b异面，
9.
【答案】
A
【考点】
直线的一般式方程与直线的平行关系
【解析】
根据直线的平行关系得到关于a的方程，解出即可．
【解答】
若直线l1：(3+a)x+4y−5+3a＝0与l2:2x+(5+a)y+8＝0平行，
则3+a2=45+a，
解得：a＝−1或a＝−7，
10.
【答案】
C
【考点】
平面的基本性质及推论
【解析】
直接利用平面的性质的应用，共面的条件的应用求出结果．
【解答】
对于选项A：当三点共线时，不能确定一个平面，故错误．
对于选项B：当该点在直线上时，不能确定一个平面，故错误．
对于选项C：由于梯形由两条对边平行，所以确定的平面有且只有一个，故另两条边也在该平面上，故正确．
对于选项D：当圆心和圆上的两点在同一条线上时，不能确定一个平面，故错误．
11.
【答案】
B
【考点】
棱柱、棱锥、棱台的体积
直线与平面所成的角
命题的真假判断与应用
【解析】
直接利用线面夹角判定A的结论，直接利用异面直线的夹角判定C的结论，直接利用几何体的体积公式求出三棱柱的体积判定D的结论，直接利用点到平面的距离判定B的结论．
【解答】
对于B：连接BC1，交CB1于点E，由于BC1⊥CB1，且平面ABC1D1⊥平面BCC1，所以CE⊥平面ABC1D1，即CE=12B1C=22，故B正确（1）对于C：条异面直线D1C和BC1所成的角，即异面直线D1C与AD1所成的角，连接AC，所以△ACD1为等边三角形，所以夹角为π3，故C错误（2）对于D:VAA1D1−BB1C1=12×1×1×1=12，故D错误．
故选：B．
12.
【答案】
B
【考点】
平面的基本性质及推论
【解析】
由直线AB平行于平面EFGH，且平面ABC交平面EFGH于HG，所以HG // AB，同理EF // AB，FG // CD，EH // CD，所以FG // EH，EF // HG．四边形EFGH为平行四边形．又AD＝BD，AC＝BC的对称性，可知AB⊥CD．从而四边形EFGH为矩形．建立二次函数关系求解四边形EFGH面积的最大值．
【解答】
∵ 直线AB平行于平面EFGH，且平面ABC交平面EFGH于HG，
∴ HG // AB，
同理：EF // AB，FG // CD，EH // CD，
∴ FG // EH，EF // HG．
∴ 四边形EFGH为平行四边形．
又∵ AD＝BD，AC＝BC的对称性，可知AB⊥CD．
∴ 四边形EFGH为矩形．
设BF:BD＝BG:BC＝FG:CD＝x，(0≤x≤1)，
∴ FG＝3x，HG＝3(1−x)，
∴ SEFGH=FG⋅HG=9x(1−x)=−9(x−12)2+94,0当x=12时，四边形EFGH的面积有最大值94．
二、填空题：（每小题5分，共计20分）
【答案】
π4
【考点】
直线的图象特征与倾斜角、斜率的关系
【解析】
先求出直线的斜率，再求直线的倾斜角．
【解答】
∵ 直线x−y＝0的斜率为1，又0≤α<π，
∴ α=π4．
【答案】
(3, 1)
【考点】
直线系方程
【解析】
直线y＝k(x−3)+1方程可化为：y−1＝k(x−3)，令y−1=0x−3=0 ，即可求出定点坐标．
【解答】
直线y＝k(x−3)+1方程可化为：y−1＝k(x−3)，
所以当y−1=0x−3=0 时，方程恒成立，解得x=3y=1 ，
所以所有直线都经过定点(3, 1)．
【答案】
3x−2y+6＝0
【考点】
直线的截距式方程
【解析】
由题意利用用截距式求直线的方程，再化为一般式．
【解答】
∵ 直线l在x轴上的截距是−2，在y轴上的截距是3，
则直线l的方程是x−2+y3=1，即 3x−2y+6＝0，
【答案】
2
【考点】
旋转体（圆柱、圆锥、圆台）
【解析】
根据题意，该四面体内接于圆锥的内切球，通过内切球即可得到a的最大值．
【解答】
依题意，四面体可以在圆锥内任意转动，故该四面体内接于圆锥的内切球，
设球心为P，球的半径为r，下底面半径为R，轴截面上球与圆锥母线的切点为Q，圆锥的轴截面如图：
则OA＝OB=32，
因为SO=332，
故可得：SA＝SB=SO2+OB2=3，
所以：三角形SAB为等边三角形，
故P是△SAB的中心，
连接BP，则BP平分∠SBA，
所以∠PBO＝30∘；
所以tan30∘=rR，即r=33R=33×32=32，
即四面体的外接球的半径为r=32．
另正四面体可以从正方体中截得，如图：
从图中可以得到，当正四面体的棱长为a时，截得它的正方体的棱长为22a，
而正四面体的四个顶点都在正方体上，
故正四面体的外接球即为截得它的正方体的外接球，
所以2r=3AA1=3×22a=62a，
所以a=2．
即a的最大值为2．
三、解答题：（写出必要的解题步骤和文字说明，共计70分）
【答案】
如图所示，
取AC的中点为O，连接PO、OB，
由PA＝PC，得AC⊥PO，由BA＝BC，得AC⊥OB，
又∵ PO∩OB＝O，∴ AC⊥平面POB，
而PB⊂平面POB，∴ AC⊥PB，
即PB⊥AC；
由（1）知，PO⊥AC，
又平面APC⊥平面ABC，且平面APC∩平面ABC＝AC，
∴ PO⊥平面ABC，
由已知可得，PO=3，S△ABC=12×2×2×32=3，
∴ VP−ABC=13S△ABC×PO=13×3×3=1．
【考点】
棱柱、棱锥、棱台的体积
直线与平面垂直
【解析】
（1）取AC的中点为O，连接PO、OB，由已知可得AC⊥PO，AC⊥OB，由直线与平面垂直的判定可得AC⊥平面POB，进一步得到PB⊥AC；
（2）由（1）知，PO⊥AC，再由平面与平面垂直的性质可得PO⊥平面ABC，然后利用棱锥体积公式求解三棱锥P−ABC的体积．
【解答】
如图所示，
取AC的中点为O，连接PO、OB，
由PA＝PC，得AC⊥PO，由BA＝BC，得AC⊥OB，
又∵ PO∩OB＝O，∴ AC⊥平面POB，
而PB⊂平面POB，∴ AC⊥PB，
即PB⊥AC；
由（1）知，PO⊥AC，
又平面APC⊥平面ABC，且平面APC∩平面ABC＝AC，
∴ PO⊥平面ABC，
由已知可得，PO=3，S△ABC=12×2×2×32=3，
∴ VP−ABC=13S△ABC×PO=13×3×3=1．
【答案】
（1）F、G、H的位置如图；
证明：(Ⅱ)连接BD，设O是BD的中点，
∵ BC的中点为M、GH的中点为N，
∴ OM // CD，OM=12CD，
HN // CD，HN=12CD，
∴ OM // HN，OM＝HN，
即四边形MNHO是平行四边形，
∴ MN // OH，
∵ MN⊄平面BDH；OH⊂面BDH，
∴ 直线MN // 平面BDH；
(Ⅲ)方法一：
连接AC，过M作MH⊥AC于P，
则正方体ABCD−EFGH中，AC // EG，
∴ MP⊥EG，
过P作PK⊥EG于K，连接KM，
∴ EG⊥平面PKM
则KM⊥EG，
则∠PKM是二面角A−EG−M的平面角，
设AD＝2，则CM＝1，PK＝2，
在Rt△CMP中，PM＝CMsin45∘=22，
在Rt△PKM中，KM=PK2+PM2=322，
∴ cs∠PKM=PKKM=223，
即二面角A−EG−M的余弦值为223．
方法二：以D为坐标原点，
分别为DA，DC，DH方向为x，y，z轴建立空间坐标系如图：
设AD＝2，则M(1, 2, 0)，G(0, 2, 2)，E(2, 0, 2)，O(1, 1, 0)，
则GE→=(2, −2, 0)，MG→=(−1,0,2)，
设平面EGM的法向量为n→=(x, y, z)，
则n→⋅GE→=0n→⋅MG→=0 ，即2x−2y=0−x+2z=0 ，令x＝2，得n→=(2, 2, 1)，
在正方体中，DO⊥平面AEGC，
则m→=DO→=(1, 1, 0)是平面AEG的一个法向量，
则cs=m→⋅n→|m→||n→|=2+29×2=432=223．
二面角A−EG−M的余弦值为223．
【考点】
二面角的平面角及求法
直线与平面平行
【解析】
(Ⅰ)根据展开图和直观图之间的关系进行判断即可；
(Ⅱ)利用线面平行的判定定理即可证明直线MN // 平面BDH；
(Ⅲ)法一：利用定义法求出二面角的平面角进行求解．
法二：建立坐标系，利用向量法进行求解即可．
【解答】
（1）F、G、H的位置如图；
证明：(Ⅱ)连接BD，设O是BD的中点，
∵ BC的中点为M、GH的中点为N，
∴ OM // CD，OM=12CD，
HN // CD，HN=12CD，
∴ OM // HN，OM＝HN，
即四边形MNHO是平行四边形，
∴ MN // OH，
∵ MN⊄平面BDH；OH⊂面BDH，
∴ 直线MN // 平面BDH；
(Ⅲ)方法一：
连接AC，过M作MH⊥AC于P，
则正方体ABCD−EFGH中，AC // EG，
∴ MP⊥EG，
过P作PK⊥EG于K，连接KM，
∴ EG⊥平面PKM
则KM⊥EG，
则∠PKM是二面角A−EG−M的平面角，
设AD＝2，则CM＝1，PK＝2，
在Rt△CMP中，PM＝CMsin45∘=22，
在Rt△PKM中，KM=PK2+PM2=322，
∴ cs∠PKM=PKKM=223，
即二面角A−EG−M的余弦值为223．
方法二：以D为坐标原点，
分别为DA，DC，DH方向为x，y，z轴建立空间坐标系如图：
设AD＝2，则M(1, 2, 0)，G(0, 2, 2)，E(2, 0, 2)，O(1, 1, 0)，
则GE→=(2, −2, 0)，MG→=(−1,0,2)，
设平面EGM的法向量为n→=(x, y, z)，
则n→⋅GE→=0n→⋅MG→=0 ，即2x−2y=0−x+2z=0 ，令x＝2，得n→=(2, 2, 1)，
在正方体中，DO⊥平面AEGC，
则m→=DO→=(1, 1, 0)是平面AEG的一个法向量，
则cs=m→⋅n→|m→||n→|=2+29×2=432=223．
二面角A−EG−M的余弦值为223．
【答案】
∵ ΔABC的三个顶点A(−1, 0)，B(5, −4)，C(1, 2)，
故BC边上的中点D(3, −1)，
故BC边上的中线的长度AD=(−1−3)2+(0+1)2=17，
BC边上的中线AD所在直线方程为 y−0−1−0=x+13+1，即 x+4y+1＝0．
由于AB边所在的直线方程为 y−0−4−0=x+15+1，即 2x+3y+2＝0，
故AB边上的高线的长度，即点C(1, 2)到直线 2x+3y+2＝0的距离，
为|2+6+2|4+9=101313．
【考点】
直线的一般式方程与直线的性质
【解析】
（1）先求出BC边上的中点D的坐标，再利用两点间的距离公式求得BC边上的中线的长度AD的值；再利用两点式求出BC边上的中线AD所在直线方程．
（2）先利用两点式求出AB边所在的直线方程，再利用点到直线的距离公式求得C(1, 2)到直线 2x+3y+2＝0的距离，即为AB边上的高线的长度．
【解答】
∵ ΔABC的三个顶点A(−1, 0)，B(5, −4)，C(1, 2)，
故BC边上的中点D(3, −1)，
故BC边上的中线的长度AD=(−1−3)2+(0+1)2=17，
BC边上的中线AD所在直线方程为 y−0−1−0=x+13+1，即 x+4y+1＝0．
由于AB边所在的直线方程为 y−0−4−0=x+15+1，即 2x+3y+2＝0，
故AB边上的高线的长度，即点C(1, 2)到直线 2x+3y+2＝0的距离，
为|2+6+2|4+9=101313．
【答案】
根据不等式x−y≥0x+y+2≥0x−2≤0 可画出该不等式表示的平面区域如下图阴影部分所示：
平移y＝2x的图象得到y＝2x−z，当y＝2x−z经过点A(2, −4)时，z取最小值，−z取最大值，
∴ z的最大值为：z＝2x−y＝4+4＝8．
【考点】
简单线性规划
【解析】
（1）根据不等式组即可画出约束条件所表示的平面区域；
（2）根据平面区域，作直线y＝2x，然后平移y＝2x得到y＝2x−z，从而看出−z取最小值时，z取最大值，根据平面区域可看出y＝2x−z经过点(2, −4)时z取最小值，从而得出答案．
【解答】
根据不等式x−y≥0x+y+2≥0x−2≤0 可画出该不等式表示的平面区域如下图阴影部分所示：
平移y＝2x的图象得到y＝2x−z，当y＝2x−z经过点A(2, −4)时，z取最小值，−z取最大值，
∴ z的最大值为：z＝2x−y＝4+4＝8．
【答案】
解：(1)取AB中点M，连接CM，DM，有MD // AB1，
∵ AC=BC，∴ CM⊥AB，
又∵ 三棱柱ABC−A1B1C1为直三棱柱，
∴ 平面ABC⊥平面ABB1A1，
又∵ 平面ABC∩平面ABB1A1=AB，
∴ CM⊥平面ABB1A1，
又∵ DE⊂平面ABB1A1，
∴ CM⊥DE，
又∵ DE⊥CD，CD∩CM=C，CD⊂平面CMD，CM⊂平面CMD，
∴ DE⊥平面CMD，
又∵ MD⊂平面CMD，
∴ DE⊥MD，
∵ MD // AB1，∴ DE⊥AB1，
连接A1B交AB1于点O，∵ ABB1A1为正方形，
∴ A1B⊥AB1，
又∵ DE⊂平面ABB1A1，A1B⊂平面AA1B1B，
∴ DE // A1B，
又∵ D为BB1的中点，
∴ E为OB1的中点，
∴ EB1AB1=14．
(2)如图，以M为坐标原点，分别以MA，MO，MC为
x轴，y轴，z轴，建立空间直角坐标系，
设AB=2a，由(1)可知∠CDM=45∘，
∴ AB1=22a，
∴ DM=CM=2a，
∴ A(a, 0, 0)，B1(−a, 2a, 0)，C1(0, 2a, 2a)，
D(−a, a, 0)，E(−12a, 32a, 0)，
∴ AB1→=(−2a, 2a, 0)，B1C1→=(a, 0, 2a)，DE→=(12a, 12a, 0)，
设平面AB1C1的法向量为n→=(x, y, z)，则n→⋅AB1→=0，n→⋅B1C1→=0.
即−2x+2y=0,x+2z=0, 令z=−1可得n→=(2, 2, −1)．
∴ cs=DE→⋅n→|DE→||n→|=222×5=255．
即直线DE与平面AB1C1所成角的正弦值为255．
【考点】
用空间向量求直线与平面的夹角
两条直线垂直的判定
直线与平面垂直的判定
【解析】

【解答】
解：(1)取AB中点M，连接CM，DM，有MD // AB1，
∵ AC=BC，∴ CM⊥AB，
又∵ 三棱柱ABC−A1B1C1为直三棱柱，
∴ 平面ABC⊥平面ABB1A1，
又∵ 平面ABC∩平面ABB1A1=AB，
∴ CM⊥平面ABB1A1，
又∵ DE⊂平面ABB1A1，
∴ CM⊥DE，
又∵ DE⊥CD，CD∩CM=C，CD⊂平面CMD，CM⊂平面CMD，
∴ DE⊥平面CMD，
又∵ MD⊂平面CMD，
∴ DE⊥MD，
∵ MD // AB1，∴ DE⊥AB1，
连接A1B交AB1于点O，∵ ABB1A1为正方形，
∴ A1B⊥AB1，
又∵ DE⊂平面ABB1A1，A1B⊂平面AA1B1B，
∴ DE // A1B，
又∵ D为BB1的中点，
∴ E为OB1的中点，
∴ EB1AB1=14．
(2)如图，以M为坐标原点，分别以MA，MO，MC为
x轴，y轴，z轴，建立空间直角坐标系，
设AB=2a，由(1)可知∠CDM=45∘，
∴ AB1=22a，
∴ DM=CM=2a，
∴ A(a, 0, 0)，B1(−a, 2a, 0)，C1(0, 2a, 2a)，
D(−a, a, 0)，E(−12a, 32a, 0)，
∴ AB1→=(−2a, 2a, 0)，B1C1→=(a, 0, 2a)，DE→=(12a, 12a, 0)，
设平面AB1C1的法向量为n→=(x, y, z)，则n→⋅AB1→=0，n→⋅B1C1→=0.
即−2x+2y=0,x+2z=0, 令z=−1可得n→=(2, 2, −1)．
∴ cs=DE→⋅n→|DE→||n→|=222×5=255．
即直线DE与平面AB1C1所成角的正弦值为255．
【答案】
（1）证明：以D为原点，射线DA，DC，DD1分别为x，y，z轴的正半轴，建立坐标系，则B(2, 2, 0)，C1(0, 2, 2)，E(2, 1, 0)，F(1, 0, 0)，P(0, 0, λ)，
∴ BC1→=(−2, 0, 2)，FP→=(−1, 0, λ)，FE→=(1, 1, 0)
λ＝1时，BC1→=(−2, 0, 2)，FP→=(−1, 0, 1)，
∴ BC1→=2FP→，
∴ BC1 // FP，
∵ FP⊂平面EFPQ，BC1⊄平面EFPQ，
∴ 直线BC1 // 平面EFPQ；
（2）设平面EFPQ的一个法向量为m→=(x, y, z)，则x+y=0−x+λz=0 ，
∴ 取m→=(λ, −λ, 1)．
同理可得平面MNPQ的一个法向量为n→=(λ−2, 2−λ, 1)，
若存在λ，使面EFPQ与面PQMN所成的二面角为直二面角，则
m→⋅n→=λ(λ−2)−λ(2−λ)+1＝0，∴ λ＝1±22．
∴ 存在λ＝1±22，使面EFPQ与面PQMN所成的二面角为直二面角．
【考点】
二面角的平面角及求法
直线与平面平行
【解析】
(Ⅰ)建立坐标系，求出BC1→=2FP→，可得BC1 // FP，利用线面平行的判定定理，可以证明直线BC1 // 平面EFPQ；
(Ⅱ)求出平面EFPQ的一个法向量、平面MNPQ的一个法向量，利用面EFPQ与面PQMN所成的二面角为直二面角，建立方程，即可得出结论．
【解答】
（1）证明：以D为原点，射线DA，DC，DD1分别为x，y，z轴的正半轴，建立坐标系，则B(2, 2, 0)，C1(0, 2, 2)，E(2, 1, 0)，F(1, 0, 0)，P(0, 0, λ)，
∴ BC1→=(−2, 0, 2)，FP→=(−1, 0, λ)，FE→=(1, 1, 0)
λ＝1时，BC1→=(−2, 0, 2)，FP→=(−1, 0, 1)，
∴ BC1→=2FP→，
∴ BC1 // FP，
∵ FP⊂平面EFPQ，BC1⊄平面EFPQ，
∴ 直线BC1 // 平面EFPQ；
（2）设平面EFPQ的一个法向量为m→=(x, y, z)，则x+y=0−x+λz=0 ，
∴ 取m→=(λ, −λ, 1)．
同理可得平面MNPQ的一个法向量为n→=(λ−2, 2−λ, 1)，
若存在λ，使面EFPQ与面PQMN所成的二面角为直二面角，则
m→⋅n→=λ(λ−2)−λ(2−λ)+1＝0，∴ λ＝1±22．
∴ 存在λ＝1±22，使面EFPQ与面PQMN所成的二面角为直二面角．