高中数学人教B版 (2019)必修 第二册4.7 数学建模活动:生长规律的描述多媒体教学ppt课件

这是一份高中数学人教B版 (2019)必修 第二册4.7 数学建模活动:生长规律的描述多媒体教学ppt课件，共52页。

1.对数函数函数y=lgax_____________称为对数函数,其中a是常数,a>0且a≠1.
【思考】(1)对数函数的定义域是什么?为什么?提示:定义域为x>0,因为负数和零没有对数.(2)对数函数的解析式有何特征?提示:①a>0,且a≠1;②lgax的系数为1;③自变量x的系数为1.
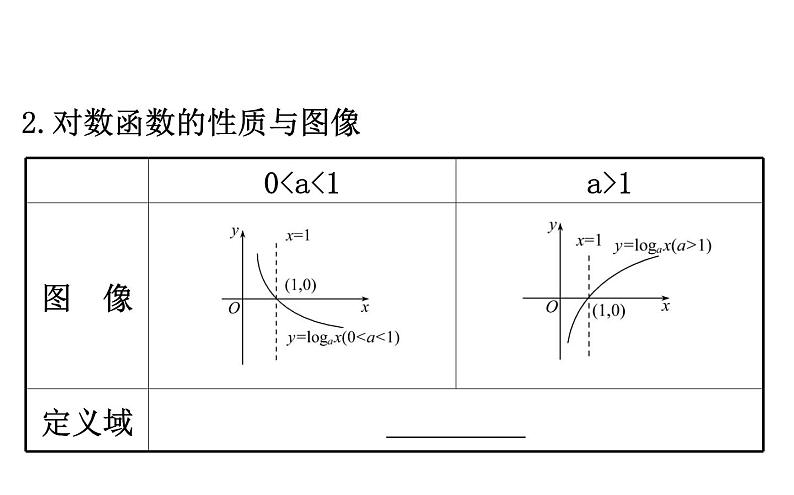
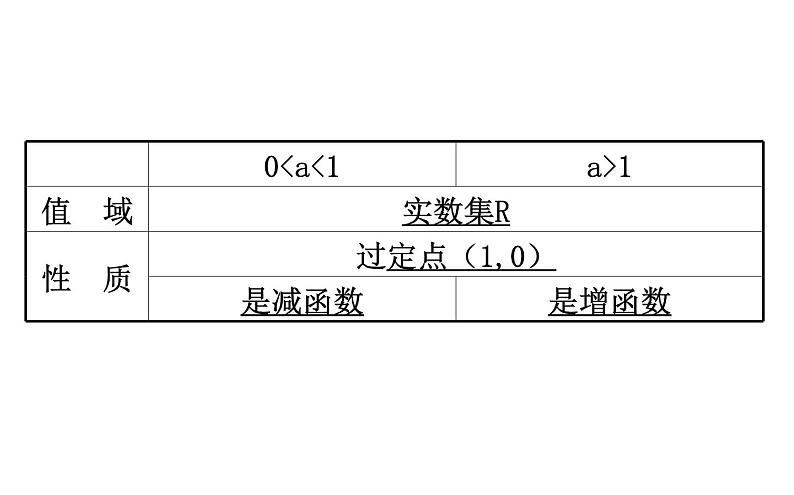
2.对数函数的性质与图像
【思考】(1)对于对数函数y=lg2x,y=lg3x,y= ,y=…,为什么一定过点(1,0) ?提示:当x=1时,lga1=0恒成立,即对数函数的图像一定过点(1,0).
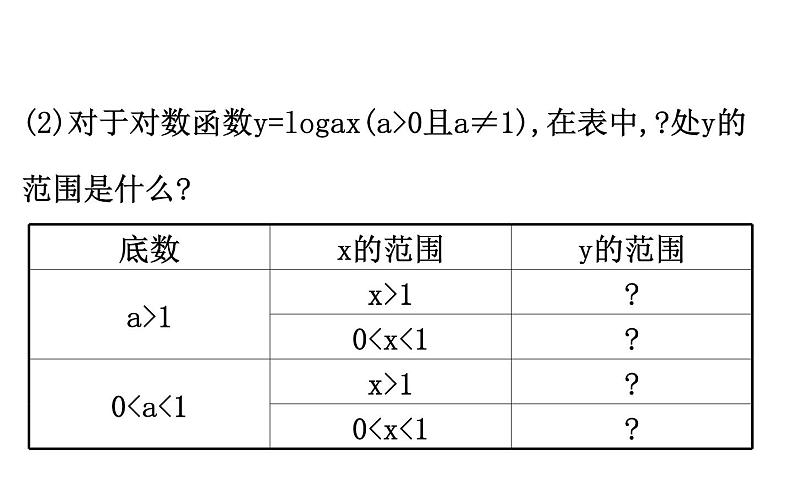
(2)对于对数函数y=lgax(a>0且a≠1),在表中,?处y的范围是什么?
【素养小测】1.思维辨析(对的打“√”,错的打“×”)(1)y=lgx5是对数函数.(　　)(2)对数函数的图像都过定点(0,1).(　　)(3)对数函数的图像都在y 轴的右侧.(　　)
提示:(1)×.y=lgx5不是对数函数,对数函数的底数是常数,真数为自变量.(2)×.对数函数的图像都过定点(0,1).(3)√.由对数函数的图像可知正确.
2.函数y=lg2x在区间(0,2]上的最大值是(　　)A.2　B.1　C.0　　D.-1【解析】选B.函数y=lg2x在(0,2]上递增,故x=2时,y的值最大,最大值是1.
3.函数y=lg3x与y= 的图像关于________对称. 【解析】函数y=lg3x与y= 的图像关于x轴对称.答案:x轴
类型一　利用对数函数的单调性比较大小【典例】1.若a=lg32,b=lg34,c= ,则a,b,c的大小关系正确的是(　　)A.a2.设a=lg32,b=lg2 ,c=2lg32,则a,b,c的大小关系是(　　)A.a【思维·引】1.同底数的利用单调性比较大小,不同底数的化同底后比较.2.借助中间值比较大小.
【解析】1.选C.因为函数y=lg3x是增函数,所以lg34>lg32>lg31=0,c= =-lg36<0,所以c1,所以a,b,c的大小关系为b【内化·悟】1.对数函数底数不同时,用哪个公式化为同底?提示:可以利用公式 2.对数式比较大小一般用什么方法?提示:利用单调性、中间值比较.
【类题·通】　比较对数值大小时常用的四种方法(1)同底数的利用对数函数的单调性.(2)同真数的利用对数函数的图像或用换底公式转化.(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.提醒:比较数的大小时先利用性质比较出与零或1的大小.
【习练·破】1.(2019·烟台高一检测)若a=2-0.3,b=lg23,c=lg47,则a,b,c的大小关系为(　　)A.a【解析】选D.因为0c=lg47>lg44=1,所以a,b,c的大小关系为a2.(2019·重庆高一检测)设a=lg2e,b=ln 3e,c=e-2(e为自然对数的底数),则a,b,c的大小关系为(　　)A.a>b>c B.c>a>bC.b>c>a D.b>a>c
【解析】选D.因为lg22=12,c=e-2a>c.
【加练·固】已知 ,则(　　)A.2a>2b>2c　　　　　　B.2b>2a>2cC.2c>2b>2aD.2c>2a>2b
【解析】选B.由于函数y= 为减函数,因此由 ,可得b>a>c,又由于函数y=2x为增函数,所以2b>2a>2c.
类型二　解对数不等式【典例】1.(2019·南平高一检测)已知函数f(x)=ln x,若f(x-1)<1,则实数x的取值范围是(　　) A.(-∞,e+1)B.(0,+∞)C.(1,e+1)　D.(e+1,+∞)
2. 已知lga(3x+1)【思维·引】1.列出相应的不等式,利用单调性求解.2.利用单调性、定义域转化为不等式组求解.
【解析】1.选C.因为函数f(x)=ln x,f(x-1)<1,所以ln(x-1)<1,因为函数f(x)=ln x是增函数,而且定义域为(0,+∞ ),所以02.(1)当a>1时,函数y=lgax是增函数,而且定义域为(0,+∞ ),所以0<3x+1<7-5x,即 解得
(2)当07-5x>0,即 解得
【内化·悟】解含对数的不等式时容易忽视什么问题?提示:容易忽视定义域.
【类题·通】　关于对数不等式的解法(1)整理不等式,考查对数式的底数,确定单调性,不确定的分情况讨论.(2)根据单调性、定义域列出不等式(组),解不等式(组)求范围.
【习练·破】已知lg3(2m2+2m-1)>lg3(m-1),求m的取值范围.【解析】函数y=lg3x是增函数,而且定义域为(0,+∞),所以2m2+2m-1>m-1>0,即 解得m>1.
【加练·固】已知lga(3a-1)恒为正,则a的取值范围是________. 
【解析】由题意知lga(3a-1)>0=lga1.当a>1时,y=lgax是增函数且定义域为(0,+∞),所以 解得a> ,所以a>1;当0综上所述,a的取值范围是 或a>1.答案: 或a>1
类型三　对数型函数的定义域角度1　简单的对数型函数的定义域【典例】函数y=lg2(x2+5x+6)的定义域为________. 【思维·引】利用真数大于0解不等式求范围.
【解析】令x2+5x+6>0,解得x<-3或x>-2, 所以函数的定义域为(－∞,－3)∪(－2,+∞). 答案: (－∞,－3)∪(－2,+∞).
【素养·探】在求对数型函数的定义域时,常常用到核心素养中的数学运算,通过解不等式或不等式组求定义域.将本例中的函数变为y=lg(x-1)(x2+5x+6),试求函数的定义域.
【解析】由题意 解得 所以x>1,且x≠2,所以函数的定义域为(1,2)∪(2,+∞).
角度2　综合的对数型函数的定义域【典例】1.函数f(x)= +lg(3x+1)的定义域是________. 2.函数y= +ln(3-2x)的定义域为________. 
【思维·引】1.利用分母不为零、被开方数不小于零、真数大于零求定义域.2.利用被开方数不小于零,真数大于零列不等式组求解.
【解析】1.由 解得 2.由 解得 所以0≤x< ,所以函数的定义域为 .答案:
【类题·通】求对数型函数的定义域时应遵循的原则(1)分母不能为0.(2)根指数为偶数时,被开方数非负.(3)对数的真数大于0,底数大于0且不为1.
【习练·破】1.(2019·抚顺高一检测)函数y= +lg(1+x)的定义域为________. 2.函数y= (16-4x)的定义域为________. 
【解析】1.由题意得 解得-12.由 得 所以函数的定义域为(-1,0)∪(0,2).答案:(-1,0)∪(0,2)
【加练·固】(2019·长沙高一检测)函数f(x)= +lg(1+x)的定义域是(　　)A.(-∞,-1)　　　　　B.(1,+∞)C.(-1,1)∪(1,+∞) D.(-∞,+∞)