数学八年级上册17.1 等腰三角形习题课件ppt

这是一份数学八年级上册17.1 等腰三角形习题课件ppt，共29页。PPT课件主要包含了答案显示，见习题，答案B，答案C，PD∥OB等内容，欢迎下载使用。

(1)PD∥OB　(2)等腰
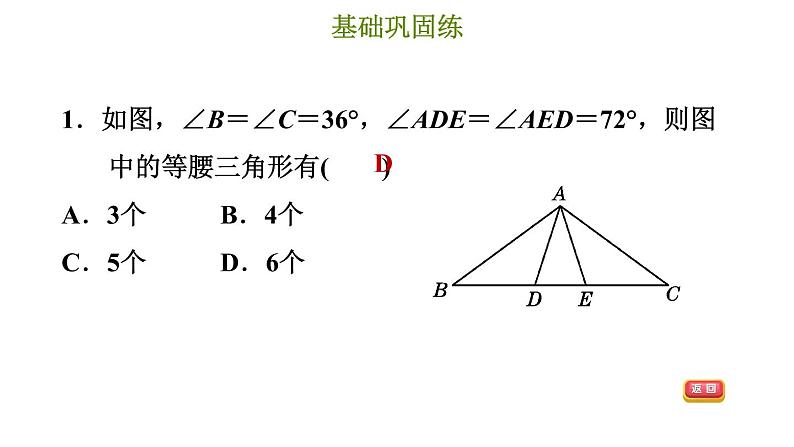
1．如图，∠B＝∠C＝36°，∠ADE＝∠AED＝72°，则图中的等腰三角形有(　　)A．3个 B．4个 C．5个 D．6个
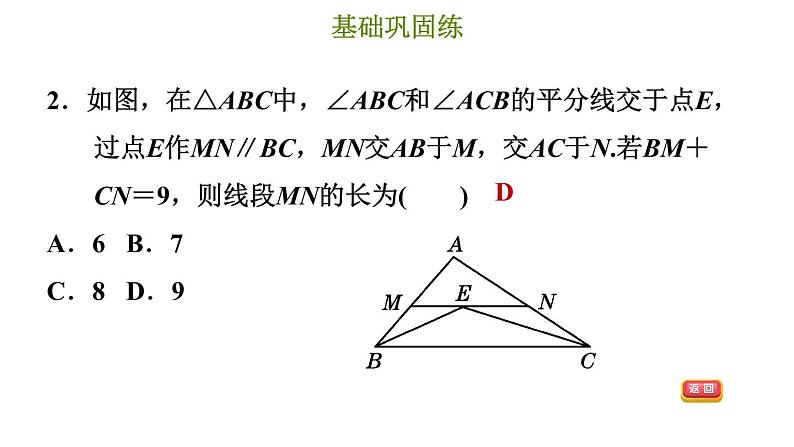
2．如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC，MN交AB于M，交AC于N.若BM＋CN＝9，则线段MN的长为(　　)A．6 B．7 C．8 D．9
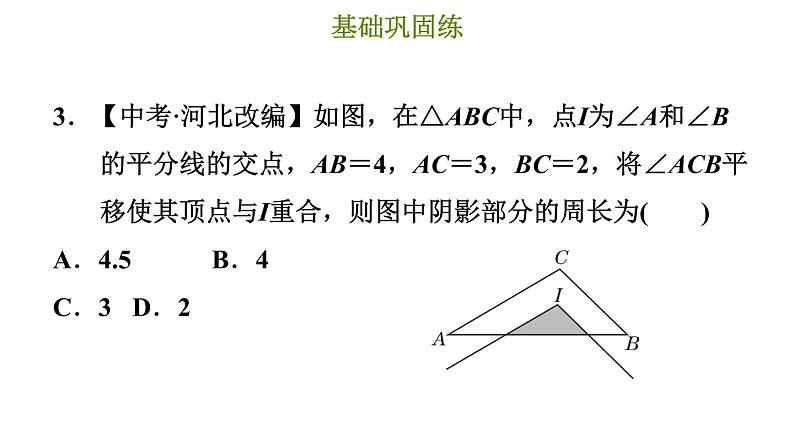
3．【中考·河北改编】如图，在△ABC中，点I为∠A和∠B的平分线的交点，AB＝4，AC＝3，BC＝2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为(　　)A．4.5 B．4 C．3 D．2
【点拨】如图，设∠ACB平移后与AB交于D，E两点．连接AI，BI. ∵点I为∠CAB和∠CBA的平分线的交点，∴∠CAI＝∠BAI，∠CBI＝∠ABI.由平移得AC∥DI，∴∠CAI＝∠AID，∴∠BAI＝∠AID，∴AD＝DI，同理可得BE＝EI，∴△DIE的周长＝DE＋DI＋EI＝DE＋AD＋BE＝AB＝4.即图中阴影部分的周长为4.
5．【创新考法】课堂上老师用投影给大家展示了一道习题：已知∠AOB，作∠AOB的平分线OC，将直尺DEMN如图所示摆放，使EM边与OB边重合，顶点D落在OA边上，DN边与OC交于点P.试判断△DOP的形状．(1)认真审题，这把直尺提供条件：_____________________.(2)△DOP是________三角形.
6．在△ABC中，AB＝AC，∠A＝∠C，则△ABC是(　　)A．等腰三角形 B．等边三角形C．直角三角形 D．不能确定
7．如图，在等边三角形ABC中，BC＝2，CD平分∠ACB，CD交AB于点D，DE∥BC，则△ADE的周长为(　　)A．2 B．2.5 C．3 D．4
8．如图，D，E，F分别是等边三角形ABC各边上的点，且AD＝BE＝CF，则△DEF的形状是(　　)A．等边三角形B．腰和底边不相等的等腰三角形C．直角三角形D．不等边三角形
9．【易错：未分类讨论导致漏解】如图所示的正方形网格中，网格线的交点称为格点，已知A，B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是(　　)A．6 B．7 C．8 D．9
10．【2019·河北唐山路北区模拟】如图，等边三角形ABC的边长是2，CH是边AB上的高，点M是CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接MN，则在点M的运动过程中，线段MN长度的最小值是(　　)
11．【教材改编题】如图，BD＝BC，∠A＝ ∠C，BD是∠ABC的平分线．(1)求证：AB＝AC；
(2)求△ABC各内角的度数．
解：设∠ABD＝x，则∠CBD＝∠A＝x，∴∠C＝2x.在△ABC中，x＋x＋x＋2x＝180°，解得x＝36°，∴∠A＝36°，∠ABC＝∠C＝72°.
证明：如图，∵DE∥AC，∴∠1＝∠3.∵AD平分∠BAC，∴∠1＝∠2，∴∠2＝∠3.∵AD⊥BD，∴∠2＋∠B＝90°，∠3＋∠BDE＝90°，∴∠B＝∠BDE，∴BE＝DE，∴△BDE是等腰三角形．
12．【中考·四川内江】如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC.求证：△BDE是等腰三角形．
13．数学课上，李老师给出了下面的题目．在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC.试确定线段AE与DB的大小关系，并说明理由．小敏与同桌小聪讨论后，进行了如下解答：
(1)特殊情况，探究结论：如图①，当点E为AB的中点时，请你直接写出结论：AE______DB(填“＞”“＜”或“＝”)．
(2)特例启发，解答题目：解：题目中，AE与DB的大小关系：AE______DB(填“＞”“＜”或“＝”)．理由如下：如图②，过点E作EF∥BC，EF交AC于点F.(请你完成解答过程)
【点拨】要判断AE与DB是否相等，就需要判断AE，DB所在三角形是否全等或AE，DB是否分别等于第三条线段．在本题中，结合已知条件，特殊情况时，可证明DB＝EB，而AE＝EB，可知AE＝DB.一般情况时，需作EF∥BC，证明AE＝EF及△DBE≌△EFC即可．
解：由题意得∠ABC＝∠ACB＝∠A＝60°，AB＝BC＝AC.∵EF∥BC，易得∠AEF＝∠AFE＝∠A＝60°.∴AE＝AF＝EF. ∴AB－AE＝AC－AF，即BE＝CF.∵ED＝EC，∴∠D＝∠ECB.又∵∠D＋∠BED＝∠ABC＝60°，∠ECB＋∠FCE＝∠ACB＝60°，∴∠BED＝∠FCE.∴△DBE≌△EFC.∴DB＝EF.∴AE＝DB.
14．如图，在△ABC中，AB＝AC，∠A＝100°，BE平分∠ABC，BE交AC于点E.(1)求证：BC＝BE＋AE.
证明：在BC上截取BD＝BE，连接DE，如图所示．∵AB＝AC，∠BAC＝100°，∴∠ABC＝∠C＝(180°－100°)÷2＝40°.∵BE平分∠ABC，∴∠CBE＝∠ABE＝20°.∵BD＝BE，∴∠BDE＝∠BED＝(180°－20°)÷2＝80°.又∵∠BDE＝∠C＋∠CED，∠C＝40°，∴∠CED＝40°＝∠C. ∴DE＝DC.过点E作EM⊥BA，交BA的延长线于点M，过点E作EN⊥BC于点N.
(2)探究：若∠A＝108°，则BC的长等于哪两条线段长的和呢？试说明理由．
解：BC＝CE＋AB或BC＝CE＋AC.理由如下：在CB上截取CP＝CE，连接PE，如图所示．∵AB＝AC，∠A＝108°，∴∠ABC＝∠C＝(180°－108°)÷2＝36°.∵CP＝CE，∴∠CPE＝∠CEP＝(180°－36°)÷2＝72°.∴∠BPE＝180°－72°＝108°. ∴∠BPE＝∠A.