初中数学人教版七年级下册7.2.2用坐标表示平移集体备课课件ppt

这是一份初中数学人教版七年级下册7.2.2用坐标表示平移集体备课课件ppt，共43页。PPT课件主要包含了学习目标，图形在坐标系中的平移，沿x轴平移，沿y轴平移，向右平移，向左平移，向上平移，向下平移，回顾旧知，导入新知等内容，欢迎下载使用。

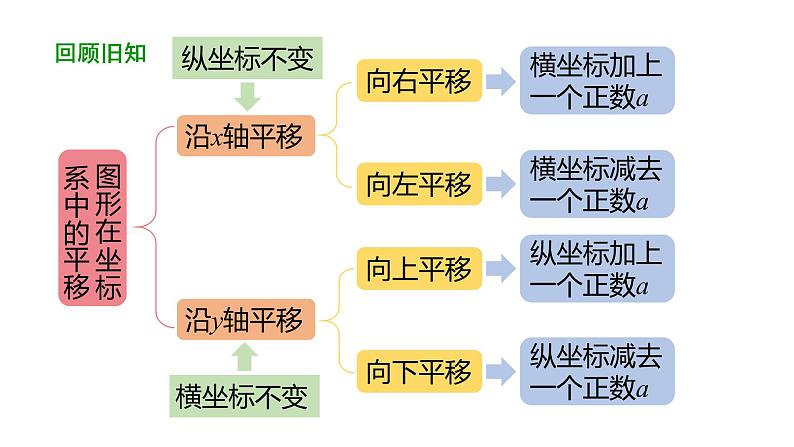
1.掌握点的坐标的变化引起的平面直角坐标系中点或图形平移的规律。2.进一步体会平面直角坐标系是数与形之间的桥梁，感受代数与几何的相互转化，初步建立空间概念。
上一节课我们学习了图形的平移引起的图形上点的坐标的变化规律，反过来，这节课我们将探讨图形上点的坐标的某种变化引起的图形平移．
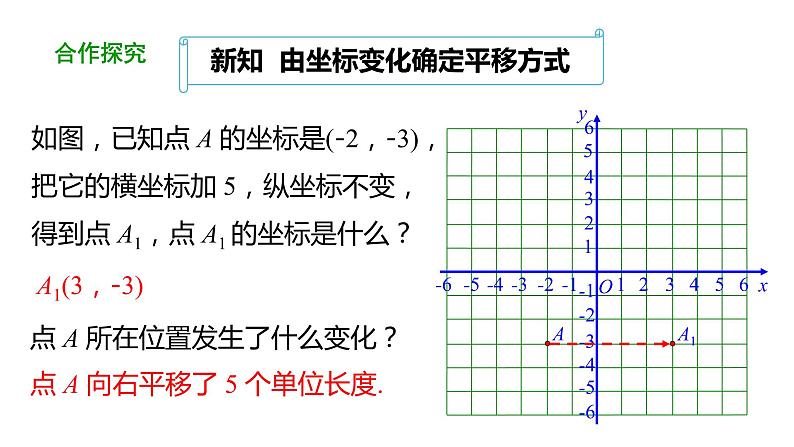
如图，已知点 A 的坐标是(-2，-3)，把它的横坐标加 5，纵坐标不变，得到点 A1，点 A1 的坐标是什么？
点 A 所在位置发生了什么变化？
点 A 向右平移了 5 个单位长度.
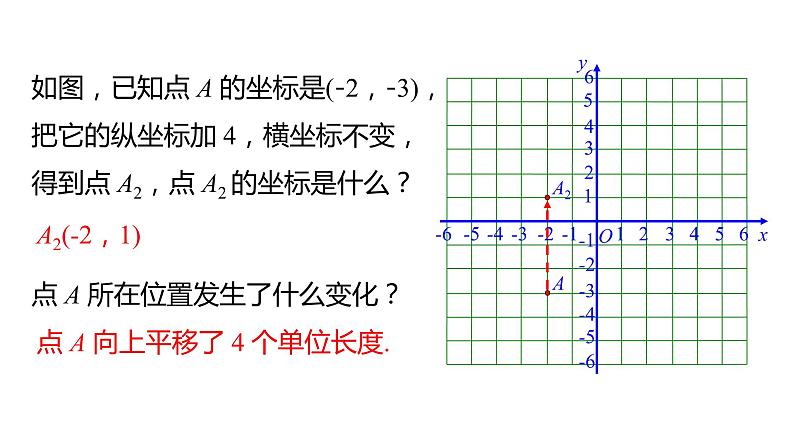
如图，已知点 A 的坐标是(-2，-3)，把它的纵坐标加 4，横坐标不变，得到点 A2，点 A2 的坐标是什么？
点 A 向上平移了 4 个单位长度.
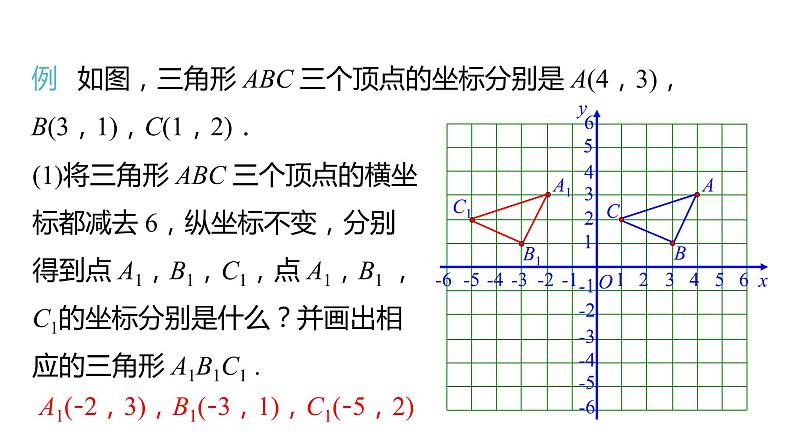
(1)将三角形 ABC 三个顶点的横坐标都减去 6，纵坐标不变，分别得到点 A1，B1，C1，点 A1，B1 ，C1的坐标分别是什么？并画出相应的三角形 A1B1C1 .
A1(-2，3)，B1(-3，1)，C1(-5，2)
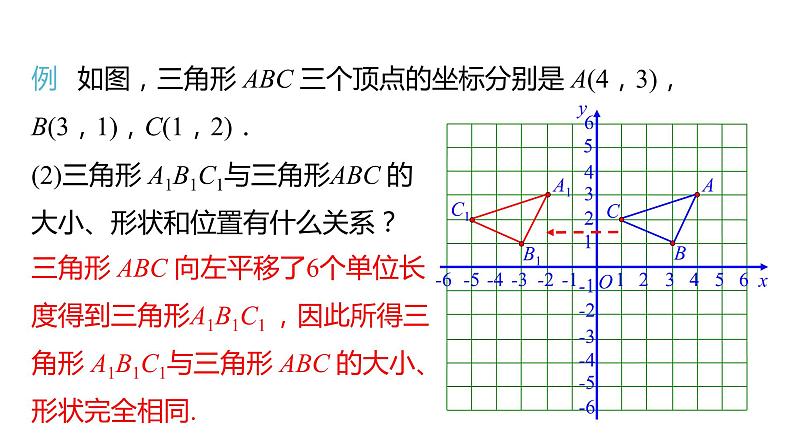
例 如图，三角形 ABC 三个顶点的坐标分别是 A(4，3)，B(3，1)，C(1，2)．
(2)三角形 A1B1C1与三角形ABC 的大小、形状和位置有什么关系？
三角形 ABC 向左平移了6个单位长度得到三角形A1B1C1 ，因此所得三角形 A1B1C1与三角形 ABC 的大小、形状完全相同.
(3)若三角形 ABC 三个顶点的横坐标都加 2，纵坐标不变呢？画出得到的图形.
A1(6，3)，B1(5，1)，C1(3，2)
在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减去)一个正数 a，相应的新图形就是把原图形向右(或向左)平移 a 个单位长度.
(1)将三角形 ABC 三个顶点的纵坐标都减去 5，横坐标不变，分别得到点 A2，B2，C2，点 A2，B2 ，C2 坐标分别是什么？并画出相应的三角形 A2B2C2 .
A2(4，-2)，B2(3，-4)，C2(1，-3)
(2)三角形 A2B2C2与三角形ABC 的大小、形状和位置有什么关系？
三角形 ABC 向下平移了5个单位长度得到三角形A2B2C2 ，因此所得三角形 A2B2C2与三角形 ABC 的大小、形状完全相同.
(3)若三角形 ABC 三个顶点的纵坐标都加 2，横坐标不变呢？画出得到的图形.
A2(4，5)，B2(3，3)，C2(1，4)
在平面直角坐标系内，如果把一个图形的各个点的纵坐标都加(或减去)一个正数 b，相应的新图形就是把原图形向上(或向下)平移 b 个单位长度．
思考 如图，将三角形 ABC 三个顶点的横坐标都减去 6，同时纵坐标减去 5，能得到什么结论？画出得到的图形.
所得三角形可以由三角形 ABC 向左平移 6 个单位长度，再向下平移 5个单位长度得到.两个三角形的大小、形状完全相同.
一个图形依次沿 x 轴方向、y 轴方向平移后所得图形上的点与原来图形对应点(x，y)的坐标之间的关系：
向右平移 a 个单位长度，向上平移 b 个单位长度
向右平移 a 个单位长度，向下平移 b 个单位长度
向左平移 a 个单位长度，向上平移 b 个单位长度
向左平移 a 个单位长度，向下平移 b 个单位长度
点 N(-1，3)可以看作由点 M(-1，-1)( )A. 向上平移 4 个单位长度得到的B. 向左平移 4 个单位长度得到的C. 向下平移 4 个单位长度得到的D. 向右平移 4 个单位长度得到的
1.在平面直角坐标系中，三角形 ABC 的三个顶点的横坐标保持不变，纵坐标都减去 3，则得到的新三角形与原三角形相比，向( ) 平移了 3 个单位长度.A.左B.右C.下D.上
2.如图，与图 1 中的三角形相比，图 2 中的三角形发生的位置变化是( )A.向左平移 3 个单位长度B.向左平移 1 个单位长度C.向上平移 3 个单位长度D.向下平移 1 个单位长度
3.在平面直角坐标系中，三角形 ABC 的三个顶点的位置如图所示，点 A' 的坐标是(-2，2)，现将三角形 ABC 平移，使点 A 变换为点 A' ，点 B' ， C' 分别是 B，C 的对应点.(1)试说明三角形 ABC 经过怎样的平移得到三角形 A'B'C' ；
解：(1)将三角形 ABC 先向左平移 5 个单位长度，再向下平移 2 个单位长度得到三角形 A'B'C'.
3.在平面直角坐标系中，三角形 ABC 的三个顶点的位置如图所示，点 A' 的坐标是(-2，2)，现将三角形 ABC 平移，使点 A 变换为点 A' ，点 B' ， C' 分别是 B，C 的对应点.(2)请画出平移后的三角形 A'B'C' ，并写出点 B'，C' 的坐标；
解：(2) 三角形 A'B'C' 如图所示.B'(-4，1)，C'(-1，-1).
3.在平面直角坐标系中，三角形 ABC 的三个顶点的位置如图所示，点 A' 的坐标是(-2，2)，现将三角形 ABC 平移，使点 A 变换为点 A' ，点 B' ， C' 分别是 B，C 的对应点.(3)若三角形 ABC 内部一点 P 的坐标为(a，b)，则点 P 的对应点 P' 的坐标是__________.
先向左平移 5 个单位长度，再向下平移 2 个单位长度.
1．点M向左平移4个单位长度后的坐标是(－1，2)，则点M原来的坐标是( )A．(－5，2) B．(3，2)C．(－1，6) D．(－1，－2)2．在平面直角坐标系中，将点A(－1，－2)向右平移3个单位长度后得到点B，则点B关于x轴的对称点B′的坐标为( )A．(－3，－2) B．(2，2)C．(－2，2) D．(2，－2)
3．在平面直角坐标系中有一点A(－2，1)，将点A先向右平移3个单位长度，再向下平移2个单位长度，则点A平移后的坐标为____________．4．(2017·平塘县期末)点P(m＋2，2m＋1)向右平移1个单位长度后，正好落在y轴上，则m＝______．
5．将某个图形的各顶点的横坐标减去3，纵坐标保持不变，即是将该图形( )A．向右平移3个单位长度B．向左平移3个单位长度C．向上平移3个单位长度D．向下平移3个单位长度
6．(2017·大连)在平面直角坐标系xOy中，线段AB的两个端点坐标分别为A(－1，－1)，B(1，2)．平移线段AB，得到线段A′B′.已知点A′的坐标为(3，－1)，则点B′的坐标为( )A．(4，2) B．(5，2)C．(6，2) D．(5，3)
7．如图所示，三角形OAB的顶点B的坐标为(4，0)，把三角形OAB沿x轴向右平移得到三角形CDE，如果CB＝1，那么OE的长为____．
8．如图，三角形AOC是一个直角三角形，C(0，3)，A(－2，0)，把三角形AOC沿AC边平移，使点A平移到点C，三角形AOC变换为三角形CED，则D，E的坐标分别为_________，_________．
9．如图，三角形A1B1C1是由三角形ABC经过平移得到的．(1)请你写出平移的过程；(2)如果点N是由点M经过上述平移得到的，点N的坐标为(a，b)，求点M的坐标．
解：(1)三角形ABC向上平移3个单位长度，再向右平移6个单位长度．(2)M(a－6，b－3)．
10．如图，把图①中的三角形ABC经过一定的变换得到图②中的三角形A′B′C′，如果图①中三角形ABC边上的点P的坐标为(a，b)，那么这个点在图②中的对应点P′的坐标为( )A．(a－2，b－3) B．(a－3，b－2)C．(a＋3，b＋2) D．(a＋2，b＋3)
11．(2017·邵阳)如图所示，三架飞机P，Q，R保持编队飞行，某时刻在坐标系中的坐标分别为(－1，1)，(－3，1)，(－1，－1).30秒后，飞机P飞到P′(4，3)位置，则飞机Q，R的位置Q′，R′分别为( )A．Q′(2，3)，R′(4，1)B．Q′(2，3)，R′(2，1)C．Q′(2，2)，R′(4，1)D．Q′(3，3)，R′(3，1)
14．在平面直角坐标系中，平行四边形的位置如图所示．(1)写出A，B，C，D四点的坐标；(2)将平行四边形ABCD向下平移3个单位长度，得到平行四边形A1B1C1D1，画出相应图形，并写出各点坐标；(3)将平行四边形ABCD向左平移6个单位长度，得到平行四边形A2B2C2D2，画出相应图形，并写出各点坐标；(4)你认为怎样建立直角坐标系，A，B，C，D四个顶点的坐标最简单？
解：(1)A(1，－2)，B(5，－2)，C(7，1)，D(3，1)．(2)如图所示，A1(1，－5)，B1(5，－5)，C1(7，－2)，D1(3，－2)．(3)平行四边形A2，B2，C2，D2，如图所示，A2(－5，－2)，B2(－1，－2)，C2(1，1)，D2(－3，1)．(4)以点A为坐标原点，直线AB为x轴，建立平面直角坐标系．
15．将三角形ABC上任意一点P0(x0，y0)按下述规律平移：P0(x0，y0)→P1(x0＋3，y0－2)，画出新的三角形A1B1C1，并写出A1，B1，C1的坐标．
解：三角形A1B1C1如图所示，A1(2，2)，B1(－1，－3)，C1(4，－1)．
16．如图，已知三角形ABC经过平移后得到三角形A1B1C1，点A与A1，点B与B1，点C与C1分别是对应点，观察各对应点坐标之间的关系，解答下列问题：(1)分别写出点A与A1，点B与B1，点C与C1的坐标；(2)若点P(2x，2y)通过上述的平移规律平移得到的对应点为Q(x，y)，求x，y的值．
解：(1)A(1，2)，B(2，1)，C(3，3)，A1(－2，－1)，B1(－1，－2)，C1(0，0)；(2)由图可知，三角形A1B1C1是三角形ABC先向左平移3个单位长度，再向下平移3个单位长度后得到的．∴P(2x，2y)通过上述的平移规律平移后的坐标为(2x－3，2y－3)，∴2x－3＝x，2y－3＝y，解得x＝3，y＝3.∴x的值为3，y的值为3.
解：(2)∵点P从原点出发，以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动，∴当点P移动4 s时，移动的距离为2×4＝8.∵OA＝4，OC＝6，∴当点P移动4 s时，在线段CB上，离点C的距离是8－6＝2.即点P的坐标是(2，6)．(3)当点P到x轴的距离为5个单位长度时，存在两种情况：①当点P在OC上时，点P移动的时间5÷2＝2.5(s)，②当点P在BA上时．点P移动的时间是(6＋4＋1)÷2＝5.5(s)，故在移动过程中，当点P到x轴的距离为5个单位长度时，点P移动的时间是2.5 s或5.5 s.