2019年广州市七下数学期中考试试题

这是一份2019年广州市七下数学期中考试试题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 在平面直角坐标系中，点 A3,−5 所在象限为
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

2. 3 的相反数是
A. −3B. 13C. 3D. 3

3. 下列方程中，是二元一次方程的是
A. xy=2B. 2x=yC. 2x=2D. x2=y

4. 如图，直线 AB 、 CD 相交于点 O，若 ∠1+∠2=100∘，则 ∠BOC 等于
A. 130∘B. 140∘C. 50∘D. 40∘

5. 如图，直线 a，b 被 c 所截，现给出下列四个条件：① ∠1=∠5；② ∠1=∠7；③ ∠2+∠3=180∘；④ ∠7=∠5．其中能够说明 a∥b 的条件为
A. ①②B. ①③C. ①④D. ③④

6. 下列各命题中，属于真命题的是
A. 两个锐角之和为钝角B. 相等的两个角是对顶角
C. 同位角相等D. 钝角大于它的补角

7. 下列各组解中，不是二元一次方程 x+2y=5 的解的是
A. x=1,y=2B. x=6,y=−1C. x=2,y=1.5D. x=9,y=−2

8. 将三角形 ABC 三个顶点的纵坐标分别加 3，横坐标不变，连接三个新得到的点所成的三角形是原图形
A. 向左平移 3 个单位得到B. 向右平移 3 个单位得到
C. 向上平移 3 个单位得到D. 向下平移 3 个单位得到

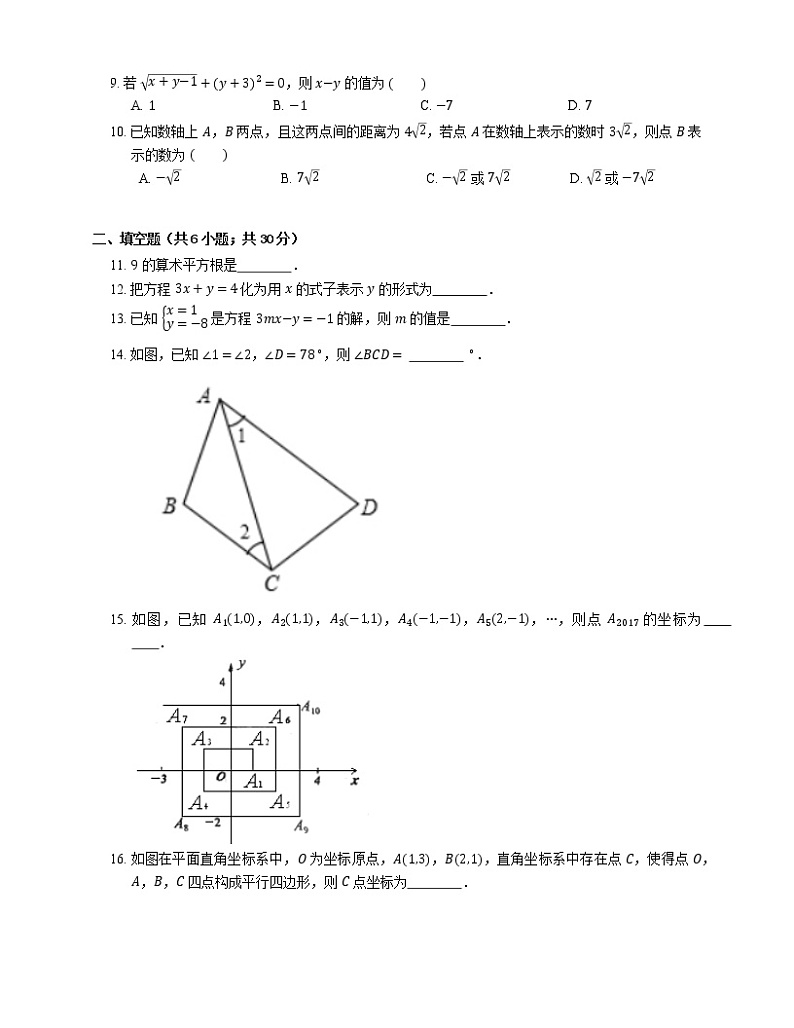
9. 若 x+y−1+y+32=0，则 x−y 的值为
A. 1B. −1C. −7D. 7

10. 已知数轴上 A，B 两点，且这两点间的距离为 42，若点 A 在数轴上表示的数时 32，则点 B 表示的数为
A. −2B. 72C. −2 或 72D. 2 或 −72

二、填空题（共6小题；共30分）
11. 9 的算术平方根是 ．

12. 把方程 3x+y=4 化为用 x 的式子表示 y 的形式为 ．

13. 已知 x=1y=−8 是方程 3mx−y=−1 的解，则 m 的值是 ．

14. 如图，已知 ∠1=∠2，∠D=78∘，则 ∠BCD= ∘．

15. 如图，已知 A11,0，A21,1，A3−1,1，A4−1,−1，A52,−1，⋯，则点 A2017 的坐标为 ．

16. 如图在平面直角坐标系中，O 为坐标原点，A1,3，B2,1，直角坐标系中存在点 C，使得点 O，A，B，C 四点构成平行四边形，则 C 点坐标为 ．

三、解答题（共8小题；共104分）
17. 计算：
（1）33+5−23+35；
（2）327+3−2−4．

18. 解二元一次方程组．
（1）2x−y=5,7x−3y=20.（要求用代入消元法）
（2）−2x+5y=7,−2x+y=3.

19. 如图，梯形 ABCD 中，AD∥BC，E 在 BC 上，且 ∠A+∠1=180∘，则 AB∥DE．理由如下：
∵AD∥BC（ ）．
∴∠ +∠B=180∘（ ）．
又 ∵∠A+∠1=180∘（ ）．
∴ ．
∴AB∥DE（ ）．

20. 在边长为 1 的小正方形网格中，△AOB 的顶点均在格点上．
（1）请写出点 A，B 的坐标；
（2）将 △AOB 向左平移 3 个单位长度得到 △A1O1B1，请画出 △A1O1B1；
（3）求 △ABO 的面积．

21. 某停车场的收费标准如下：中型汽车的停车费为 6 元/辆，小型汽车的停车费为 4 元/辆，现在停车场有 50 辆中、小型汽车，这些车共缴纳停车费 230 元，问中、小型汽车各有多少辆?

22. 如图，已知 ∠ABC 的平分线 BD 和 ∠ACE 的平分线 CD 相交于 D，∠DBC=∠D．
（1）AB 与 CD 平行吗?请说明理由；
（2）如果 ∠A=54∘，求 ∠D 的度数．

23. 已知关于 x，y 的方程组 3x+2y=m+1,4x+3y=m−1.
（1）当 2m−6=0 时，求这个方程组的解；
（2）在（1）的条件下，如果三角形 ABO 的顶点坐标分别是 Ax,0，B0,y，O0,0，那么三角形 AOB 的面积是多少?

24. 如图，在平面直角坐标系中，已知 Aa,0，Bb,0，其中 a，b 满足 ∣a+1∣+b−32=0．
（1）填空：a= ，b= ．
（2）如果在第三象限内有一点 M−2,m，请用含 m 的式子表示 △ABM 的面积；
（3）在（2）条件下，当 m=−32 时，在 y 轴上有一点 P，使得 △BMP 的面积与 △ABM 的面积相等，请求出点 P 的坐标．
答案
第一部分
1. D
2. A
3. B
4. A
5. A
6. D
7. B
8. C
9. D
10. C
第二部分
11. 3
12. y=−3x+4
13. −3
14. 102∘
15. 505,−504
16. 3,4 或 1,−2 或 −1,2
第三部分
17. （1） 原式=33−23+5+35=3+45.
（2） 原式=3+2−3−2=3−3.
18. （1）
2x−y=5, ⋯⋯①7x−3y=20. ⋯⋯②
由 ① 得：
y=2x−5. ⋯⋯③
将 ③ 代入 ② 得：
7x−32x−5=20x=5.
将 x=5 代入 ③ 得：
y=10−5=5.∴
原方程组的解为
x=5,y=5.
（2）
−2x+5y=7, ⋯⋯①−2x+y=3. ⋯⋯②∴
原方程组的解为
x=−1,y=1.
19. 已知；A；两直线平行，同旁内角互补；已知；∠1=∠B；同位角相等，两直线平行
20. （1） A1,3，B3,2．
（2） △A1O1B1 为所求．
（3） 过点 A 作 AC⊥x 轴，过点 B 作 BD⊥x 轴，
∴AC=3，BD=2，OC=1，CD=2，OD=3，
∴S△ABO=S△ACO+S矩形ACDB−S△BDO=12AC×CO+12AC+BD×CD−12OD×BD=12×3×1+12×3+2×2−12×2×3=72.
21. 设中型汽车有 x 辆、小型汽车有 y 辆，
根据题意可得：
x+y=50,6x+4y=350.
解得
x=15,y=35.
答：中型汽车有 15 辆、小型汽车有 35 辆．
22. （1） AB∥CD．
∵BD 平分 ∠ABC，
∴∠ABD=∠DBC，
又 ∵∠DBC=∠D，
∴∠ABD=∠D，
∴AB∥CD．
（2） ∵AB∥CD（已证），
∴∠ACD=∠A=54∘（两直线平行，内错角相等），
又 ∵CD 平分 ∠ACE（已知），
∴∠DCE=∠ACD=54∘，
∴∠ABC=∠DCE=54∘（两直线平行，同位角相等），
∠D=12∠ABC=27∘．
23. （1） 由 2m−6=0 得 m=3，
把 m=3 代入原方程得 3x+2y=4,4x+3y=2.
解方程组得：x=8,y=−10.
（2） 由（1）可得 A8,0，B0,−10，
∣OA∣=8，∣OB∣=10，
S△AOB=12∣OA∣×∣OB∣=40．
答：三角形 AOB 的面积是 40．
24. （1） −1；3
（2） 过点 M 作 MN⊥x 轴于点 N，
∵A−1,0，B3,0，
∴AB=1+3=4，
又 ∵ 点 M−2,m 在第三象限，
∴MN=∣m∣=−m，
S△ABM=12AB⋅MN=12×4×−m=−2m.
（3） 当 m=−32 时，M−2,−32，
∴S△ABM=−2m=−2×−32=3，
点 P 有两种情况，
①当点 P 在 y 轴正半轴上时，设点 P0,k，
S△BMP=5×32−12×2⋅32+k−12×5×32−12×3⋅k=−52k+94.
∵S△ABM=S△BMP，
∴−52k+94=3，k=0.3，
∴ 点 P10,0.3．
②当点 P 在 y 轴负半轴上时，设点 P0,n，
S△BMP=5×n−12×2⋅−n−32−12×5×32−12×3⋅−n=−52n−94.
∵S△ABM=S△BMP，
∴−52n−94=3，n=−2.1，
∴ 点 P20,−2.1．