2018-2019学年上海市杨浦区七下期中数学试卷

这是一份2018-2019学年上海市杨浦区七下期中数学试卷，共11页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。

一、填空题（共14小题；共70分）
1. 36 的平方根是 ．

2. 若 x4=16，则 x= ．

3. 把 537 化成幂的形式是 ．

4. 计算：49−32= ．

5. 比较大小：−22 −3（填“>”，“=”，“<”）．

6. 月球沿着一定的轨道围绕地球运动，它在远地点时与地球相距的距离约为 405500 km，将该数保留三个有效数字得到的近似数为 km（用科学记数法表示）．

7. 已知数轴上 A，B 两点的距离是 3，点 A 在数轴上对应的数是 2，那么点 B 在数轴上对应的数是 ．

8. 如图，直线 AB，CD 相交，若 ∠1=100∘，则直线 AB，CD 的夹角为 ∘．

9. 如图，∠B 的内错角是 ．

10. 如图，直线 a∥b，直线 c 分别与 a，b 相交，若 ∠1=70∘，则 ∠2= ．

11. 如图，已知 DE∥BF，AC 平分 ∠BAE，∠DAB=70∘，那么 ∠ACF= ∘．

12. 如图，已知 AB∥CD，BE 平分 ∠ABD，∠DCE=150∘，则 ∠D= ∘．

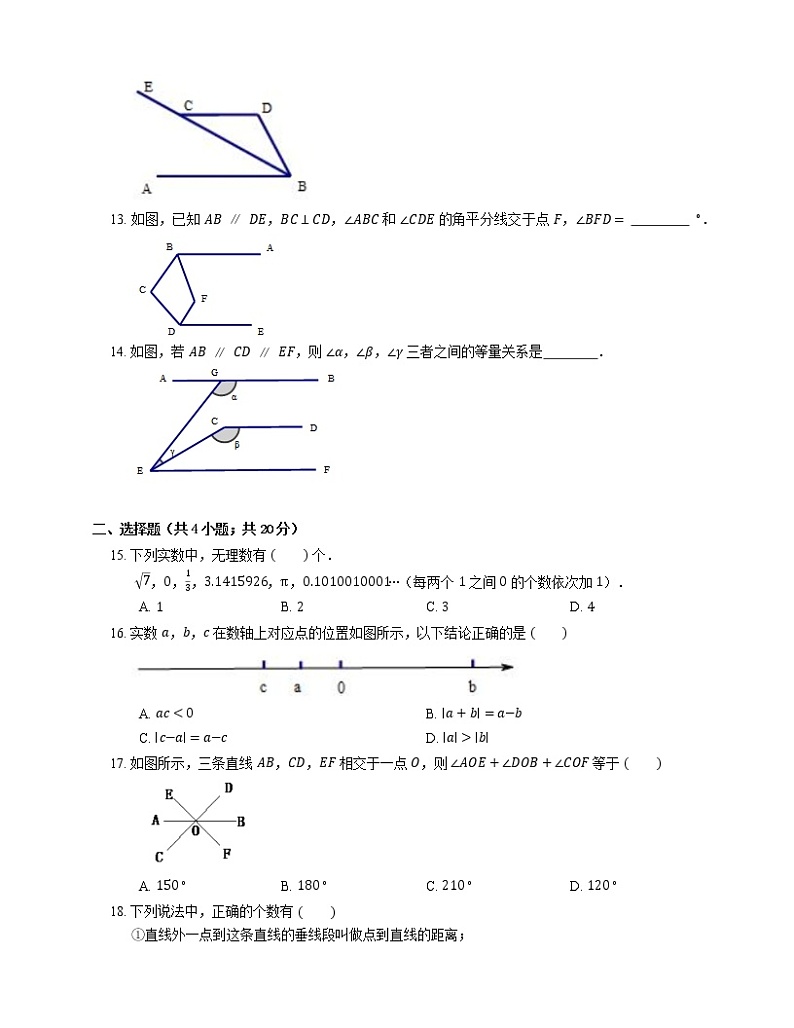
13. 如图，已知 AB∥DE，BC⊥CD，∠ABC 和 ∠CDE 的角平分线交于点 F，∠BFD= ∘．

14. 如图，若 AB∥CD∥EF，则 ∠α，∠β，∠γ 三者之间的等量关系是 ．

二、选择题（共4小题；共20分）
15. 下列实数中，无理数有 个．
7，0，13，3.1415926，π，0.1010010001⋯（每两个 1 之间 0 的个数依次加 1）．
A. 1B. 2C. 3D. 4

16. 实数 a，b，c 在数轴上对应点的位置如图所示，以下结论正确的是
A. ac<0B. ∣a+b∣=a−b
C. ∣c−a∣=a−cD. ∣a∣>∣b∣

17. 如图所示，三条直线 AB，CD，EF 相交于一点 O，则 ∠AOE+∠DOB+∠COF 等于
A. 150∘B. 180∘C. 210∘D. 120∘

18. 下列说法中，正确的个数有
①直线外一点到这条直线的垂线段叫做点到直线的距离；
②经过一点，有且只有一条直线与已知直线平行；
③两个角的两边分别平行，那么这两个角相等；
④两条平行直线被第三条直线所截，一组内错角的角平分线互相平行．
A. 1 个B. 2 个C. 3 个D. 4 个

三、解答题（共10小题；共130分）
19. 计算：23−3−1227−9．

20. 计算：3+12−13÷3．

21. 计算：2−32−2−30+212．

22. 利用幂的运算性质计算：316÷39×623．

23. 按下列要求画图并填空：如图．
（1）过点 A 画直线 BC 的平行线 AD；
（2）过点 B 画直线 AD 的垂线段，垂足为点 E；
（3）若点 B 到直线 AD 的距离为 4 cm，BC=2 cm，则 S△ABC= cm2．

24. 如图，已知 ∠1=∠3，∠2+∠3=180∘，请说明 AB 与 DE 平行的理由．
解：将 ∠2 的邻补角记作 ∠4，则
∠2+∠4=180∘（ ），
因为 ∠2+∠3=180∘（ ），
所以 ∠3=∠4（ ）．
因为 ，（已知）
所以 ∠1=∠4（ ），
所以 AB∥DE（ ）．

25. 如图，直线 AB，CD，EF 被直线 GH 所截，已知 AB∥CD，∠1+∠2=180∘，请填写 CD∥EF 的理由．
解：
因为 ∠1=∠3（ ），
（已知），
所以 ∠2+∠3=180∘（ ），
得 AB∥EF（ ），
因为 AB∥CD（ ），
所以 CD∥EF（ ）．

26. 如图，AB∥DE，∠1=∠ACB，AC 平分 ∠BAD，试说明 AD∥BC．

27. 如图，已知 AB∥CD，分别探究下列三个图形中 ∠APC 和 ∠PAB，∠PCD 的关系．
结论：
（1） ；
（2） ；
（3） ．

28. 如图，已知射线 CB∥OA，∠C=∠OAB=100∘，E，F 在 CB 上，且满足 ∠FOB=∠AOB，OE 平分 ∠COF．
（1）求 ∠EOB 的度数（直接写出结果，无需解答过程）．
∠EOB= ∘；
（2）若在 OC 右侧左右平行移动 AB，那么 ∠OBC:∠OFC 的值是否随之发生变化?若变化，请找出变化规律；若不变，请求出这个比值；
（3）在 OC 右侧左右平行移动 AB 的过程中，是否存在使 ∠OEC=∠OBA 的情况?若存在，请直接写出 ∠OEC 度数；若不存在，请说明理由．
答案
第一部分
1. ±6
【解析】因为 ±62=36，则 36 的平方根为 ±6．
2. ±2
【解析】因为 x4=16，
所以 x2=4，
所以 x=±2．
3. 375
【解析】537=375．
4. 278
【解析】原式 =14932=1493=14949=149×23=278．
5. >
【解析】∵−22=22≈2.828<−3=3，
∴−22>−3．
6. 4.06×105
【解析】405500 km=4.055×105 km≈4.06×105 km．
7. 2±3
【解析】设 B 点对应的数是 x，
∵ 数轴上 A，B 两点之间的距离为 3，点 A 对应的数是 2，
∴∣x−2∣=3，解得 x=2+3 或 x=2−3．
8. 80
【解析】∵∠1=100∘，
∴∠AOC=180∘−100∘=80∘，
∴ 直线 AB 与 CD 的夹角是 80∘．
9. ∠DAB
【解析】由图知，∠B 和 ∠DAB 是直线 CB 和 DC 被 BE 所截形成的，在截线两侧，且在两被截线之间，
∴∠B 的内错角是 ∠DAB．
10. 110∘
【解析】如图：
∵∠1=70∘，
∴∠3=∠1=70∘，
∵a∥b，
∴∠2+∠3=180∘，
∴∠2=180∘−70∘=110∘．
11. 125
【解析】∵∠DAB=70∘，
∴∠EAB=180∘−70∘=110∘，
∵AC 平分 ∠BAE，
∴∠CAE=12∠BAE=55∘，
∵DE∥BF，
∴∠ACF=180∘−∠EAC=125∘．
12. 120
【解析】∵∠DCE=150∘，
∴∠DCB=180∘−∠DCE=180∘−150∘=30∘．
∵AB∥CD，
∴∠ABE=∠DCB=30∘．
∵BE 平分 ∠ABC，
∴∠ABD=2∠ABE=2×30∘=60∘．
∵AB∥CD，
∴∠D=180∘−∠ABD=180∘−60∘=120∘．
13. 135
【解析】连接 BD．
∵∠C+∠CBD+∠CDB=180∘，BC⊥CD，
∴∠C=90∘，
∴∠CBD+∠CDB=90∘．
∵AB∥DE，
∴∠ABD+∠BDE=180∘，
∴∠CBD+∠CDB+∠ABD+∠BDE=90∘+180∘=270∘，即 ∠ABC+∠CDE=270∘．
∵∠ABC 和 ∠CDE 的平分线交于点 F，
∴∠CBF+∠CDF=12×270∘=135∘，
∴∠BFD=360∘−90∘−135∘=135∘．
14. ∠α+∠γ=∠β
【解析】∵AB∥CD∥EF，
∴∠α+∠γ+∠CEF=180∘，∠β+∠CEF=180∘，
∴∠α+∠γ+∠CEF=∠β+∠CEF，
∴∠α+∠γ=∠β．
第二部分
15. C
【解析】根据无理数的三种形式可知：7，π，0.1010010001⋯ 为无理数，共 3 个．
16. C【解析】由数轴可知，c∣c∣>∣a∣，
A．ac>0，A 错误；
B．∣a+b∣=a+b，B 错误；
C．∣c−a∣=a−c，C 正确；
D．∣b∣>∣a∣，D 错误．
17. B【解析】∵∠DOB=∠AOC，
∴∠AOE+∠DOB+∠COF=∠AOE+∠AOC+∠COF=∠EOF=180∘．故选B．
18. A【解析】①直线外一点到这条直线的垂线段长度叫做点到直线的距离，故①错误；
②经过直线外一点，有且只有一条直线与已知直线平行，故②错误；
③两个角的两边分别平行，那么这两个角相等或互补，故③错误；
④两条平行直线被第三条直线所截，一组内错角的角平分线互相平行，故④正确．
故选：A．
第三部分
19. 原式=23−3−1227+9=23−3−323+3=123.
20. 原式=3+23−33÷3=3+23−33×13=3+2−13=3+53.
21. 原式=2−3−1+2=3−2−1+2=2.
22. 原式=423÷323×623=43×623=823=4.
23. （1） 如图，AD 即为所求．
（2） 如图，BE 即为所求．
（3） 4
【解析】∵BC∥AD，
∴ 三角形 ABC 的高为 4 cm，
∴S△ABC=12×2×4=4．
24. 邻补角的定义；已知；同角的补角相等；∠1=∠3；等量代换；同位角相等，两直线平行
25. 对顶角相等；∠1+∠2=180∘；等量代换；同旁内角互补，两直线平行；已知；平行于同一条直线的两直线互相平行
26. ∵AB∥DE，
∴∠BAC=∠1，
∵∠1=∠ACB，
∴∠ACB=∠BAC，
∵∠CAB=12∠BAD，
∴∠ACB=∠DAC，
∴AD∥BC．
27. ∠A+∠P+∠C=360∘；∠APC=∠A+∠C；∠C=∠A+∠P
【解析】（1）过点 P 作 PE∥AB，则 AB∥PE∥CD，
∴∠1+∠PAB=180∘，∠2+∠PCD=180∘，
∴∠APC+∠PAB+∠PCD=360∘．
故填：∠A+∠APC+∠C=360∘；
（2）过点 P 作直线 PF∥AB，
∵AB∥CD，∴AB∥PF∥CD，
∴∠PAB=∠1，∠PCD=∠2，
∴∠APC=∠PAB+∠PCD．
故填：∠APC=∠A+∠C；
（3）∵AB∥CD，
∴∠1=∠C，
∵∠1=∠A+∠P，
∴∠C=∠A+∠P．
故填：∠C=∠A+∠P．
28. （1） 40
【解析】∵CB∥OA，∠C=∠OAB=100∘，
∴∠COA=180∘−∠C=180∘−100∘=80∘，
∵CB∥OA，
∴∠FBO=∠AOB，
又 ∵∠FOB=∠AOB，
∴∠FBO=∠FOB，
∴OB 平分 ∠AOF，
又 ∵OE 平分 ∠COF，
∴∠EOB=∠EOF+∠FOB=12∠COA=12×80∘=40∘．
（2） 不变．
∵CB∥OA，则 ∠OBC=∠BOA，∠OFC=∠FOA，
则 ∠OBC:∠OFC=∠AOB:∠FOA，
又 ∵∠FOA=∠FOB+∠AOB=2∠AOB，
∴∠OBC:∠OFC=∠AOB:∠FOA=∠AOB:2∠AOB=1:2．
（3） ∠OEC=60∘．
【解析】∵CB∥OA，∠C=∠OAB=100∘，
∴∠AOC=∠ABC=80∘，
则四边形 AOCB 为平行四边形，
则 ∠OEC=∠EOB+∠OBF=∠EOB+∠AOB，∠OBA=∠BOC=∠COE+∠EOB，
又 ∵∠OEC=∠OBA，
则 ∠AOB=∠COE，
则 ∠COE=∠EOF=∠FOB=∠AOB=80∘÷4=20∘，
则 ∠EOB=2×20∘=40∘，
此时 ∠OEC=40∘+20∘=60∘．